Una nueva prueba diagnóstica debe validarse, mediante su comparación con un estándar de referencia en un espectro apropiado de pacientes.
Las pruebas diagnósticas no son absolutamente exactas, sino que pueden existir falsos positivos y falsos negativos.
Una buena prueba diagnóstica será la que ofrezca una aceptable proporción de resultados positivos en personas enfermas y una aceptable proporción de resultados negativos en personas sanas.
La mejor medida de la utilidad de una prueba diagnóstica la constituyen los cocientes de probabilidad, que determinan cuánto más probable es el resultado de una prueba entre las personas enfermas que entre las sanas.
En el presente artículo se abordan las nociones estadísticas fundamentales para interpretar los resultados de un artículo de pruebas diagnósticas, pero con un planteamiento orientado a la clínica, dando prioridad a la comprensión de los conceptos frente a los elementos matemáticos.
A new diagnostic test needs to be validated through comparison with a reference standard in an appropriate spectrum of patients.
Diagnostic tests are not perfectly accurate; on the contrary, there can be false-positive and false-negative findings.
A good diagnostic test is that which provides an acceptable proportion of positive results when a determinate condition is present in patients and an acceptable proportion of negative results when it is absent.
The best measure of the usefulness of a diagnostic test is the likelihood ratio, which informs us to what degree a particular result is more likely in a person in whom a condition is present than in a person in whom the condition is absent.
The present article discusses the fundamental statistical concepts necessary to interpret the results section of an article about a diagnostic test; however, the approach is clearly oriented toward clinical practice, with emphasis on concepts rather than mathematics.
El diagnóstico es un proceso complejo, siempre basado en la incertidumbre. Esta incertidumbre se puede acotar por medio de instrumentos estadísticos basados en la teoría de la probabilidad1. El proceso diagnóstico supone asignar a una persona o grupo una cierta probabilidad de tener una enfermedad. Para conocer esa probabilidad es preciso obtener información. Esa información permite que aumente (confirmar la enfermedad) o disminuya (descartar la enfermedad) la probabilidad de asignar una etiqueta diagnóstica. La información diagnóstica se puede obtener tanto de exploraciones complementarias, como de síntomas o signos clínicos. Todas estas fuentes de información pueden ser consideradas test diagnósticos y sometidas a evaluación1.
Los test diagnósticos (o pruebas diagnósticas) no son absolutamente exactos, y existen situaciones en que clasifican como enferma a una persona sana (falso positivo) o bien como sana a una persona enferma (falso negativo)2. Existen diversos factores que afectan a los resultados de un test, por lo cual es necesario que una nueva prueba diagnóstica sea validada. La mayoría de los estudios de validez de test diagnósticos se realizan mediante la comparación del test con otra prueba considerada un estándar de referencia (gold standard).
Un test es válido si detecta a la mayoría de las personas con la enfermedad, descarta a la mayoría de las personas sanas y sus resultados positivos indican una alta probabilidad de que la enfermedad esté presente2. En otras palabras, un buen test diagnóstico será el que ofrezca una aceptable proporción de resultados positivos en personas enfermas y una aceptable proporción de resultados negativos en personas sanas3.
Las condiciones que se pueden exigir a un test diagnóstico para valorar su utilidad son básicamente tres: validez, precisión y seguridad3.
Por validez se entiende la capacidad de un test para medir lo que realmente debe medir. En este concepto estarán incluidas la sensibilidad y la especificidad.
Por precisión, reproducibilidad o fiabilidad se entiende la capacidad de un test para ofrecer los mismos resultados cuando se repite su aplicación. En la precisión influyen factores como la propia variabilidad biológica, las características inherentes al propio test y la influencia del observador. En el diagnóstico radiológico es importante considerar el efecto del observador, pues aunque una radiografía de tórax puede ser capaz de detectar nódulos de unas determinadas características hay que contar con la probabilidad de que el observador pueda interpretarlo erróneamente.
Por seguridad entendemos la capacidad del test para predecir la presencia o ausencia de enfermedad. Se mide mediante los valores predictivos (positivo y negativo).
Es importante considerar otros aspectos como sencillez de aplicación del test, aceptabilidad, seguridad y costes.
En este artículo se revisan los conceptos estadísticos que se emplean en la evaluación de los resultados de un test diagnóstico respecto a su precisión, validez y seguridad.
Algunas consideraciones sobre el proceso de medición de los resultados de una prueba diagnósticaEn los estudios de evaluación de pruebas diagnósticas, se compara dicha prueba con un estándar de referencia, al que se presupone superior jerarquía. Dicha comparación ha de hacerse en unas condiciones de calidad en el proceso de medida tanto de la prueba diagnóstica como del estándar de referencia. Es importante considerar que en el proceso de medición de la prueba diagnóstica o del estándar de referencia, pueden cometerse errores tanto de precisión como de validez.
La precisión se relaciona con la reproducibilidad o fiabilidad, es decir si las medidas son parecidas entre sí cuando se repiten un número determinado de veces. La validez tiene relación con la exactitud, es decir en qué medida se parecen los resultados de la prueba o el estándar de referencia a la realidad.
Aunque las condiciones en que se realizan las medidas de la prueba y el estándar de referencia son importantísimas en la calidad de los estudios sobre test diagnósticos, este artículo se centra en las medidas de comparación entre ambos. Los aspectos a considerar serán la magnitud de los resultados y su precisión, tras comprender los cuales se podrá proceder a su correcta interpretación y aplicación.
Primera medida de comparación: la fiabilidad, reproducibilidad o precisión de las medidasLa fiabilidad o precisión de una prueba viene determinada por la estabilidad de las mediciones cuando son repetidas en condiciones similares4. Diversos factores influyen en la variabilidad de las mediciones, pero son de especial consideración en el diagnóstico radiológico los relacionados con las variaciones de interpretación de los observadores: en primer lugar consigo mismo (variabilidad intraobservador); en segundo lugar con otros observadores (variabilidad interobservador).
La fiabilidad puede medirse con diversos estimadores: para variables categóricas con los índices kappa y kappa ponderado (según sean nominales u ordinales) y para variables continuas con el coeficiente de correlación intraclase4.
El índice kappa es una medida de la concordancia entre distintas mediciones, y se calcula comparando en una tabla de n x n los resultados de las diferentes interpretaciones de medida, entre un observador consigo mismo, o entre varios observadores5. A modo de orientación, se presenta en la tabla 1 una lista de categorías para interpretación del índice kappa.
El índice kappa es muy utilizado para el análisis de concordancia pues evita los problemas de interpretación de los simples porcentajes de concordancia respecto a los errores de este en los datos marginales. También tiene sus problemas de aplicabilidad, y sus detractores.
Como conclusión, es importante considerar que si un estudio aporta información sobre la fiabilidad de las mediciones en la prueba diagnóstica y en el estándar de referencia, incorpora sólidos argumentos para aceptar que sus resultados son válidos, al menos en el aspecto de la precisión de los test diagnósticos analizados.
La comparación jerárquica entre prueba diagnóstica y estándar de referenciaLa situación más simple para comparar una prueba diagnóstica con su estándar es aquella que presupone resultados dicotómicos (ambos test son positivos o negativos), y que el estándar es la prueba más próxima a la «certeza» diagnóstica. Aunque esta situación raras veces se encuentra en la práctica clínica (ciertas mediciones son «indeterminadas» y no caben en la categoría ni de positivo ni de negativo) la emplearemos por cuestiones didácticas, pues permite explicar el cálculo de los indicadores para medir la validez de una prueba diagnóstica.
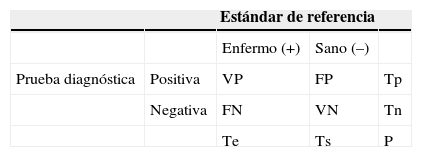
La tabla 2 explica los descriptores básicos1 y la relación entre ellos. Para que estas medidas tengan validez, es necesario (entre otras cosas) que las mediciones de la prueba diagnóstica y su estándar se realicen de manera ciega, pues la interpretación de una prueba puede verse influida si quien realiza la medición conoce previamente el resultado de su comparación.
Medidas de comparación de una prueba diagnóstica con su estándar de referencia
| Estándar de referencia | ||||
|---|---|---|---|---|
| Enfermo (+) | Sano (–) | |||
| Prueba diagnóstica | Positiva | VP | FP | Tp |
| Negativa | FN | VN | Tn | |
| Te | Ts | P | ||
FN: falso negativo; FP: falso positivo; P: población; Te: total de enfermos; Tn: total de negativos; Tp: total de positivos; Ts: total de sanos; VN: verdadero negativo; VP: verdadero positivo.
Cálculos verticales. Especificidad (Es) = VN/Ts; proporción de falsos negativos (1-Se) = Fn/Te; proporción de falsos positivos (1-Es) = FP/Ts; Sensibilidad (S) = VP/Te.
Cálculos horizontales. Valor predictivo positivo (VPP) = VP/Tp; valor predictivo negativo (VPN) = VN/Tn; prevalencia (p) = Te/P.
Para interpretar la tabla 2, se asume que el estándar de referencia establece el diagnóstico. Comparando la prueba con el estándar, observamos dos situaciones de coincidencia: los verdaderos positivos (VP), o casos en que el resultado positivo de la prueba y el estándar coinciden, y los verdaderos negativos (VN). Cuando hay discordancia encontramos casos de falsos positivos en los cuales el estándar es negativo y la prueba positiva, o falsos negativos (FN) en los que el estándar es positivo y la prueba negativa3.
Los VP son determinaciones «correctas» de la prueba y los FN son determinaciones «incorrectas» de la prueba en la población que tiene la enfermedad (casos clasificados por el estándar como enfermos).
Los VN son determinaciones «correctas» de la prueba y los FP son determinaciones «incorrectas» de la prueba en la población que no tiene la enfermedad (casos clasificados por el estándar como sanos).
Correcta e incorrecta es una forma de hablar, pues el estándar de referencia perfecto no existe y sus mediciones también están sometidas a error.
Cuando se compara una prueba con su estándar, se pueden estimar una serie de cálculos, aceptando que el estándar define el diagnóstico de la enfermedad. Si dichos cálculos se realizan desde el diagnóstico al resultado de la prueba, se hacen en sentido vertical de la tabla. Si los cálculos se realizan desde el resultado de la prueba al diagnóstico, se hacen en sentido horizontal de la tabla. Los cálculos verticales informan de la validez de la prueba, y los cálculos horizontales informan de la seguridad de la prueba.
Cálculos combinados verticales. Validez de la prueba6Siguiendo con la tabla 2, y leyendo en sentido vertical, podemos estimar una serie de probabilidades de sucesos: la probabilidad de que un caso se clasifique en cada una de las cuatro casillas en relación al total de casos de su columna. Dichas probabilidades se expresan como proporciones.
El primer cálculo que puede hacerse es la probabilidad de que la prueba identifique a una persona como enferma (prueba positiva) cuando realmente lo está (estándar positivo). Basta dividir los VP entre el total de personas con la enfermedad (Te). Este índice se denomina proporción de verdaderos positivos o sensibilidad (Se). Por tanto Se=VP/Te. Su probabilidad complementaria sería la proporción de falsos negativos (probabilidad de que la prueba clasifique a una persona como sana cuando realmente tiene la enfermedad). Por tanto 1-Se=FN/Te. Una prueba muy sensible tendrá una alta probabilidad de verdaderos positivos y una baja probabilidad de falsos negativos: una prueba sensible, cuando es negativa descarta con una alta probabilidad la presencia de enfermedad. Puede usarse la regla nemotécnica en inglés SnNout: Sn sensitivity, N negative, out. Es decir: una prueba sensible negativa descarta.
El segundo cálculo que puede hacerse es la probabilidad de que la prueba identifique a una persona como sana (prueba negativa) cuando realmente lo está (estándar negativo). Basta dividir los VN entre el total de personas sanas (Ts). Este índice se denomina proporción de verdaderos negativos o especificidad (Es). Por tanto Es=VN/Ts. Su probabilidad complementaria sería la proporción de falsos positivos (probabilidad de que la prueba clasifique a una persona como enferma cuando realmente está sana). Por tanto 1-Es=FP/Ts. Una prueba muy específica tendrá una alta probabilidad de verdaderos negativos y una baja probabilidad de falsos positivos: una prueba específica, cuando es positiva confirma con una alta probabilidad la presencia de enfermedad. Puede usarse la regla nemotécnica en inglés SpPin: Sp Specificity, P positive, in. Es decir: una prueba específica positiva confirma.
Los cálculos verticales informan de las características de una prueba diagnóstica suponiendo que conocemos previamente si la persona tiene la enfermedad. Esta situación es propia de la investigación, pero no suele ser común en la práctica clínica.
Tanto sensibilidad como especificidad son proporciones y por tanto se pueden calcular sus intervalos de confianza, igual que para cualquier proporción. Es un criterio de calidad de un estudio de validez de pruebas diagnósticas que aporte los intervalos de confianza de sus mediciones.
Cálculos combinados horizontales. Seguridad de la pruebaLeyendo la tabla 2 en sentido horizontal podemos calcular también una serie de probabilidades: la probabilidad de que un caso se clasifique en cada una de las cuatro casillas en relación al total de casos de su fila.
El primer cálculo que podemos estimar es la probabilidad de presentar la enfermedad cuando la prueba ha resultado positiva. Se define intuitivamente como proporción de enfermos entre los test positivos, y se denomina valor predictivo positivo (VPP). Por tanto VPP=VP/Tp.
El segundo cálculo que podemos estimar es la probabilidad de estar sano cuando la prueba ha resultado negativa. Se define intuitivamente como proporción de sanos entre los test negativos, y se denomina valor predictivo negativo (VPN). Por tanto VPN=VN/Tn.
Al contrario que la sensibilidad y la especificidad, que son características inherentes a la prueba, los cálculos horizontales son índices guiados por el resultado de la prueba, e informan sobre las consecuencias, en términos de probabilidad, de una prueba positiva o negativa7. Su gran ventaja es que son aplicables clínicamente, pues se basan en el proceder habitual, pero sus resultados son muy dependientes de la prevalencia de la enfermedad. Ello hace que los valores predictivos de una prueba evaluada en unas condiciones determinadas no puedan ser aplicables, en la práctica, a la misma prueba aplicada en otras condiciones diferentes, y este es precisamente el gran problema de su aplicabilidad.
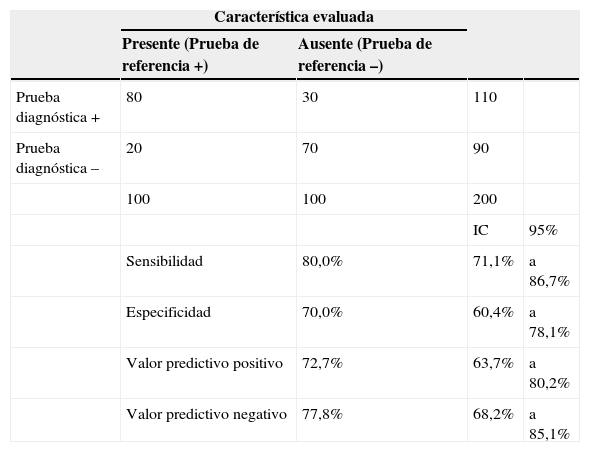
En la tabla 3 se muestra un ejemplo que aclara la influencia de la prevalencia en los valores predictivos. Podemos observar cómo al disminuir la prevalencia del 50% (100/200) al 0,99% (100/10100), permanecen casi inalterables sensibilidad y especificidad, el VPP disminuye y el VPN aumenta.
Ejemplo de la influencia de la prevalencia en los índices de comparación de una prueba diagnóstica con su estándar de referencia
| Característica evaluada | ||||
|---|---|---|---|---|
| Presente (Prueba de referencia +) | Ausente (Prueba de referencia –) | |||
| Prueba diagnóstica + | 80 | 30 | 110 | |
| Prueba diagnóstica – | 20 | 70 | 90 | |
| 100 | 100 | 200 | ||
| IC | 95% | |||
| Sensibilidad | 80,0% | 71,1% | a 86,7% | |
| Especificidad | 70,0% | 60,4% | a 78,1% | |
| Valor predictivo positivo | 72,7% | 63,7% | a 80,2% | |
| Valor predictivo negativo | 77,8% | 68,2% | a 85,1% | |
| Característica evaluada | ||||
|---|---|---|---|---|
| Presente (Prueba de referencia +) | Ausente (Prueba de referencia –) | |||
| Prueba diagnóstica + | 80 | 3000 | 3080 | |
| Prueba diagnóstica – | 20 | 7000 | 7020 | |
| 100 | 7000 | 10100 | ||
| IC | 95% | |||
| Sensibilidad | 80,0% | 71,1% | a 86,7% | |
| Especificidad | 70,0% | 69,1% | a 70,9% | |
| Valor predictivo positivo | 2,6% | 2,1% | a 3,2% | |
| Valor predictivo negativo | 99,7% | 99,6% | a 99,8% | |
Otra forma de describir el comportamiento de una prueba diagnóstica es mediante el empleo de los cocientes de probabilidad, que surgen de la necesidad de disponer de índices que no dependan de la prevalencia de la enfermedad. Los cocientes de probabilidad (llamados también likelihood ratios, razones de verosimilitud o razones de probabilidad) permiten resolver el conflicto de la combinación entre sensibilidad y especificidad1.
El cociente de probabilidad, estima cuánto más probable es el resultado de una prueba en las personas con enfermedad en relación a las personas sanas.
Existen dos tipos de cocientes de probabilidad, según los resultados posibles de la prueba: cociente de probabilidad positivo, y cociente de probabilidad negativo.
El cociente de probabilidad positivo (CP+) estima cuánto más probable es obtener un resultado positivo en sujetos enfermos que en sujetos sanos. Si nos fijamos en la tabla 2, vemos que la probabilidad de obtener un resultado positivo en sujetos enfermos equivale a la proporción de verdaderos positivos, es decir la sensibilidad (Se). La probabilidad de obtener un resultado positivo en sujetos sanos equivale a la proporción de falsos positivos, es decir el complementario de la especificidad (1-Es). Por tanto (CP+)=(Se)/(1-Es).
El cociente de probabilidad negativo (CP-) estima cuánto más probable es obtener un resultado negativo en sujetos enfermos que en sujetos sanos. La probabilidad de obtener un resultado negativo en sujetos enfermos equivale a la proporción de falsos negativos, es decir el complementario de la sensibilidad (1-Se). La probabilidad de obtener un resultado negativo en sujetos enfermos equivale a la proporción de verdaderos negativos, es decir la especificidad (Es). Por tanto (CP-)=(1-Se)/(Es).
Su interpretación es similar al riesgo relativo: los cocientes de probabilidad adoptan valores entre 0 e infinito, siendo uno el valor nulo (igualdad de probabilidad). Cuanto más se eleve el CP por encima de uno más se incrementa la probabilidad de diagnóstico; cuanto más disminuya el CP por debajo de uno más disminuirá la probabilidad de diagnóstico4. Podemos interpretarlos de la siguiente manera:
- •
CP >10: incrementos amplios de la probabilidad diagnóstica.
- •
CP 5-10: incrementos moderados de la probabilidad diagnóstica.
- •
CP 2-5: incrementos pequeños de la probabilidad diagnóstica.
- •
CP 1-2: incrementos insignificantes de la probabilidad diagnóstica.
- •
CP 1: sin cambios de la probabilidad diagnóstica.
- •
CP 0,5-1: descensos insignificantes de la probabilidad diagnóstica.
- •
CP 0,2-0,5: descensos pequeños de la probabilidad diagnóstica.
- •
CP 0,1-0,2: descensos moderados de la probabilidad diagnóstica.
- •
CP <0,1: descensos amplios de la probabilidad diagnóstica.
La principal ventaja de los cocientes de probabilidad, es que permiten calcular la probabilidad posprueba de tener la enfermedad, para un contexto en el que esta se presente con una prevalencia determinada. Conocidos los cocientes de probabilidad de una prueba diagnóstica y la probabilidad que tiene una persona de presentar una enfermedad antes de aplicar dicha prueba (probabilidad preprueba), podemos conocer mediante cálculos estadísticos (aplicación del teorema de Bayes) en qué medida cambia la probabilidad de estar enfermo si en la prueba se obtienen resultados positivos o negativos (según el cociente de probabilidad aplicado). En términos generales, el teorema de Bayes relaciona la probabilidad de un suceso frente a otro: vincula la probabilidad de un suceso A dado un suceso B con la probabilidad de B dado A.
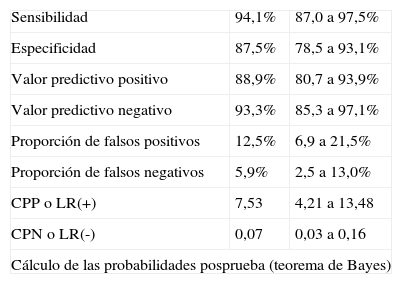
En la tabla 4 se pueden ver los cálculos bayesianos. Se parte de una prueba con unos cocientes de probabilidad determinados, y la probabilidad preprueba estimada es del 6%. Si la prueba es positiva la probabilidad de padecer la enfermedad aumenta hasta más de un 30%. En cambio si la prueba es negativa, la probabilidad de estar enfermo disminuye a menos del 0,5%. Se omitirán los cálculos estadísticos, pues en la actualidad pueden emplearse calculadoras que facilitan al clínico el proceso matemático.
Ejemplo de la aplicación de los cocientes de probabilidad para conocer la probabilidad posprueba
| Sensibilidad | 94,1% | 87,0 a 97,5% |
| Especificidad | 87,5% | 78,5 a 93,1% |
| Valor predictivo positivo | 88,9% | 80,7 a 93,9% |
| Valor predictivo negativo | 93,3% | 85,3 a 97,1% |
| Proporción de falsos positivos | 12,5% | 6,9 a 21,5% |
| Proporción de falsos negativos | 5,9% | 2,5 a 13,0% |
| CPP o LR(+) | 7,53 | 4,21 a 13,48 |
| CPN o LR(-) | 0,07 | 0,03 a 0,16 |
| Cálculo de las probabilidades posprueba (teorema de Bayes) | ||
| Probabilidad preprueba estimada | 6,0% | |
| IC 95% | ||
| Probabilidad posprueba positiva (PPPP) | 32,5% | 23,7 a 42,7% |
| 1 -PPPP | 67,5% | 57,3 a 76,3% |
| 1 - PPPN | 99,6% | 94,3 a 100, |
| Probabilidad posprueba negativa (PPPN) | 0,4% | 0,0 a 5,7% |
Apliquemos un ejemplo. La decisión clínica consiste en considerar la indicación de una angio-TC pulmonar para el diagnóstico de tromboembolismo pulmonar. Dicha prueba tiene una sensibilidad de 83% y una especificidad de 96%, con unos cocientes de probabilidad CP+ 20,74 y CP- 0,17 respectivamente8. Se atiende a un paciente que presenta un edema y enrojecimiento de toda la pierna izquierda, episodio de disnea y dolor torácico, tiene taquipnea con sat O2 98% y en la radiografía de tórax se aprecia un derrame pleural mínimo. Estimaríamos que la probabilidad de tener un tromboembolismo pulmonar, antes de hacer la prueba sería del 90%. Aplicando los CP de la angio-TC pulmonar la probabilidad posprueba, en caso de ser positiva se incrementaría al 99%. Si el resultado fuera negativo la probablidad de tener un tromboembolismo se reduciría al 59%. En este caso, en que la clínica aporta información favorable a una alta probabilidad preprueba a favor del diagnóstico el rendimiento de hacer una prueba más podría ser discutible.
Si el caso fuera un contexto de muy baja probabilidad preprueba (pongamos el 1%) la probabilidad de tener un tromboembolismo en caso de hacer una angio-TC con resultado positivo aumentaría al 18%, y se reduciría al 0,1% en caso de resultado negativo. Hacer la prueba en estas condiciones aporta un valor añadido también discutible.
Supongamos que atendemos a un paciente que tiene edema en toda la pierna, con empastamiento, se queja de accesos de tos, y la radiología es normal. Estimamos que su probabilidad de tener un tromboembolismo pulmonar es del 50%. Si la angio-TC fuese positiva la probabilidad del diagnóstico de tromboembolismo se incrementa al 95%, mientras que si fuese negativa se reduce al 15%. En condiciones de mayor incertidumbre previa, hacer una prueba con buenos cocientes de probabilidad ofrece un rendimiento mayor.
Otras ventajas de los cocientes de probabilidad son: permiten comparar pruebas entre sí o evaluar test secuenciales, son intuitivos de interpretar, y evitan el cálculo de los valores predictivos. Entre sus desventajas están la ausencia de linealidad, y la necesidad de convertir las probabilidades en odds en el cálculo de la probabilidad posprueba9.
En los estudios que evalúan pruebas diagnósticas, los cocientes de probabilidad se obtienen a partir de medidas en una muestra de una población, por lo cual siempre tienen que acompañarse del correspondiente intervalo de confianza.
Pruebas diagnósticas con resultados múltiples o continuos. Curvas ROCHasta el momento hemos analizado escenarios en que la prueba diagnóstica solamente podría tener dos resultados: positivo/negativo. Un ejemplo típico de esto sería el cultivo de una muestra biológica.
Existen muchas pruebas que se miden con una variable ordinal, o con una variable continua. Un ejemplo sería el nivel de glucemia para diagnosticar la diabetes mellitus.
La primera decisión que se podría adoptar es definir un punto de corte, o umbral de diagnóstico entre todos los valores posibles de la variable, pero suele ser una decisión difícil de tomar en la práctica pues no existe un punto de corte que discrimine perfectamente a los sujetos enfermos de los sanos. Más bien al contrario, lo que suele ocurrir es un solapamiento de los resultados de las pruebas diagnósticas en las poblaciones enferma y sana. En el ejemplo anterior, una persona podría estar sana con una glucemia basal de 128, y otra podría tener diabetes con una glucemia de 124.
Así, las características intrínsecas de la prueba (sensibilidad y especificidad) van a variar según donde se determine el punto de corte. En nuestro ejemplo, un punto de corte demasiado alto asegura una alta especificidad a costa de una baja sensibilidad (confirma la enfermedad si la prueba es positiva, pero no descarta la enfermedad si la prueba es negativa). Al contrario un punto de corte demasiado bajo asegura una alta sensibilidad, pero a costa de una baja especificidad (descarta la enfermedad si la prueba es negativa, pero no confirma la enfermedad si la prueba es positiva). De todo ello se deduce, intuitivamente, que el punto de corte ideal será el que determine el mejor equilibrio entre sensibilidad y especificidad.
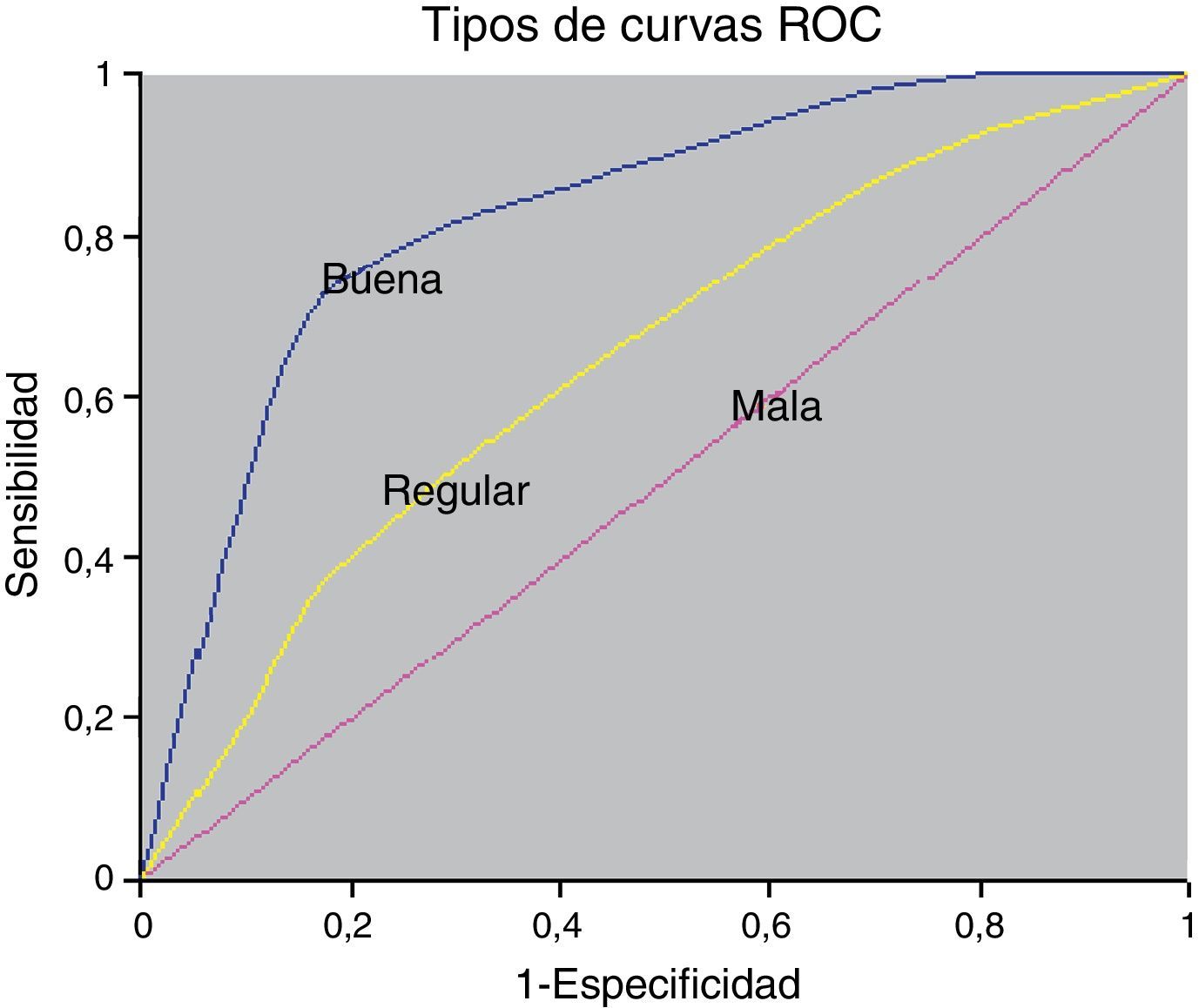
Para determinar la relación entre la sensibilidad y especificidad de una prueba, en función del umbral de diagnóstico o punto de corte, se construyen las llamadas curvas ROC (Receiving Operating Characteristics). En ellas se representan en el eje «y» los valores de la sensibilidad (Se) para cada punto de corte, y en el eje «x» los valores del complementario de la especificidad o proporción de falsos positivos (1-Es)10.
En la figura 1 se expone un ejemplo de construcción de curvas ROC. La prueba perfecta sería aquella que tuviese un punto de corte que se aproximase al 100% de Se y al 0% de proporción de falsos positivos (1-Es). En la figura puede comprobarse que las curvas ROC de una buena prueba diagnóstica son aquellas cuyo vértice se aproxima al ángulo superior izquierdo del eje de coordenadas (máxima sensibilidad y especificidad). Una prueba inútil sería aquella cuya curva ROC fuese la diagonal, pues en todos los puntos de corte coincidirían la Se (proporción de verdaderos positivos) con 1-Es (proporción de falsos positivos).
Conclusiones: puntos clave para analizar los resultados de un artículo de pruebas diagnósticas![Ejemplo de construcción de curvas ROC. Tomada de: Hrc.es (2014). Curvas ROC [online] [consultado 27 Abr 2014]. Disponible en: http://www.hrc.es/bioest/roc_1.html.](https://static.elsevier.es/multimedia/00338338/00000057000000S1/v2_201503121230/S0033833814001775/v2_201503121230/es/main.assets/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w997EogCnBdOOD93cPFbanNfYM26a8Bai41R8kcJS5RRAcnwFmMuSSo78P7nwOKMqnN0qVAs7pZqUOum9b7B7IgM3TntX8AAq6m7YhoIa5hD4goyLk7uhg41EtIHqkLAmIzNYvxYQagigvqArJDeXhc2z15hXMu9ljH1PA7RzaC9MJbJr00rd+RwPbY4TO0bMkWajkygypJaTolt4Pz5GNJIBQ/NlH3MRdE7QxT13oaMxOH+ZWTTTtr3+9wV7PaKxtdBGBsd6YRepH1cJSJVXiAg= "Ejemplo de construcción de curvas ROC. Tomada de: Hrc.es (2014). Curvas ROC [online] [consultado 27 Abr 2014]. Disponible en: http://www.hrc.es/bioest/roc_1.html.")
- •
Un artículo de evaluación de pruebas diagnósticas debe proporcionar información respecto a validez, fiabilidad y seguridad.
- •
La validez se mide con los cálculos de sensibilidad y especificidad, que deben mostrarse en los resultados o, al menos, aportar información que permita su cálculo.
- •
Es importante que aporten información sobre la fiabilidad, en especial si en la prueba intervienen observadores. La fiabilidad se mide en la mayoría de los casos mediante análisis de concordancia con el índice kappa.
- •
La seguridad se mide con el cálculo de los valores predictivos, aunque estos en la práctica tienen un valor muy limitado por ser influidos de manera importante por la prevalencia de la enfermedad.
- •
Un estudio debe proporcionar información que permita el cálculo de los cocientes de probabilidad. Si la prueba tiene varios niveles o puntos de corte, se deben poder calcular los cocientes de probabilidades correspondientes.
- •
Si la prueba diagnóstica permite obtener resultados múltiples o continuos, debe evaluarse mediante curvas ROC.
- •
Para informar de la precisión de los resultados todos los cálculos deben incorporar el intervalo de confianza.
En este artículo se ha obviado, en la medida de lo posible, describir las fórmulas para los cálculos estadísticos. Existen calculadoras disponibles en la web que permiten realizar todos los cálculos relacionados con las pruebas diagnósticas. En la página web de CASPe puede descargarse una de ellas: http://redcaspe.org/drupal/?q=node/3011.
Pueden encontrarse otros ejemplos en la literatura científica de radiología, así como referencias de interés para el radiólogo que desee profundizar en el campo de los estudios de pruebas diagnósticas12.
Responsabilidades éticasProtección de personas y animalesLos autores declaran que para esta investigación no se han realizado experimentos en seres humanos ni en animales.
Confidencialidad de los datosLos autores declaran que en este artículo no aparecen datos de pacientes.
Derecho a la privacidad y consentimiento informadoLos autores declaran que en este artículo no aparecen datos de pacientes.
Conflicto de interesesEl autor declara no tener ningún conflicto de intereses.
