Hasta el momento, se ha indicado cómo puede el farmacéutico llevar a cabo un estudio en su farmacia a partir de un conjunto de individuos que componen la muestra para extrapolar después los resultados así obtenidos al conjunto de la población diana. Este estudio aporta una gran cantidad de datos, correspondientes a las distintas variables que se han especificado previamente y que se distribuyen de una forma determinada. Pero este conjunto de valores no aportará nada a menos que se clasifiquen y agrupen en un único valor. No obstante, como el estudio se ha efectuado sobre una muestra, es preciso extrapolar esta información desde la muestra hasta la población diana, especificando el rango de valores que se estima que hay en la población.
Valores de la distribución de la muestra
Si los datos de la muestra analizada permiten suponer que se distribuyen de forma normal, se puede definir este conjunto de datos mediante dos valores muestrales fundamentales: su media (µ) y su desviación estándar o típica (σ), que ofrecen suficiente información para estimar el rango de los valores más probables. Ello se debe a que la distribución normal presenta una propiedad cardinal: se puede estimar entre qué valores se hallarán el 95% de todos sus datos, dado que el 95% de todos ellos está en el rango de su valor medio (µ) sumando y restando dos veces la desviación típica o estándar (σ).
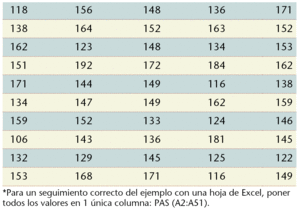
Continuemos entonces con el conjunto de datos de presión arterial sistólica (PAS) del ejemplo del tema anterior (tabla 1). Se pueden calcular mediante funciones de Excel los valores de µ [=PROMEDIO(A2:A51 )]y σ [=DESVEST(A2:A51)], con lo que se obtiene 147,66 mmHg y 18,77.
A partir de ello, el 95 % de los valores de la muestra está comprendido en el rango de:
µ ± 2*σ = 147,66 ± 2*18,77 = (110,12 ; 185,20) mmHg
De la muestra a la población: intervalo para medias
Muestras grandes, mayores de 30
Lo expuesto previamente es cierto para la muestra analizada, pero si se hubiera tomado otra muestra de la misma población diana, el valor medio y su desviación serían sensiblemente diferentes. Por ello, es preciso calcular el valor medio de las medias de cada muestra posible, es decir, el error típico o estándar (σm) que corresponde con el error medio que se hace al estimar el valor de una variable de una población completa a partir sólo de una muestra. Este parámetro se calcula mediante la fórmula: σm= σ/rn, de modo que el error típico o estándar de la población sería de:
σm= (18,77/√50) = 2,65
Con este nuevo parámetro se puede estimar el rango de valores donde hay una determinada probabilidad de contener el verdadero valor del parámetro que se estima para la población diana, es decir, el llamado intervalo de confianza (IC). El valor de la probabilidad más habitual es el 95%; en cálculos más precisos se utiliza el 99% o incluso el 99,9%. El cálculo del IC se efectúa de una forma similar a la indicada para la muestra, es decir, sumando y restando al valor de la media el doble del error estándar:
IC95 = µ ± 2*σm
Por lo que queda:
IC95 = 147,66 ± 2*2,65 = (142,36 ; 152,96) mmHg
Se observa que al ser inferior el valor de σm, el rango estimado para la población diana será entonces menor.
Este valor significa que la presión arterial diastólica de la población de referencia del estudio estará comprendida con un 95% de probabilidad en el rango estimado.
En Excel se puede estimar directamente el valor que se sumará y restará a la media, mediante una función específica [=INTERVALO.CONFIANZA(0,05;B52;B53)]. Para ello, se indicará el valor del nivel de significación (α) de 0,05 correspondiente a 100 menos la probabilidad, siempre en tanto por uno, de la desviación típica σ [=DESVEST(A2:A51)], en B52, y del tamaño de la muestra n [=CONTAR(C2:C51)], en B53.
Muestras pequeñas, menores de 30
Es probable que haya situaciones en las que no se pueda alcanzar en el estudio que se realiza el número adecuado de participantes, por lo que habría que realizarlo con un número de muestras menor al necesario. Entre otras cosas, ello implica que no se puede aplicar la metodología descrita anteriormente, que es válida para muestras grandes, o al menos de 30 o más participantes. Si se utilizara se cometería una desviación, más notable cuanto menor sea el tamaño de nuestra muestra y mayor dispersión haya. Por este motivo se analiza de una forma especial, mediante la t de Student.
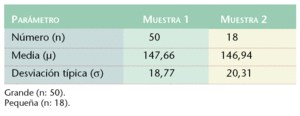
Imaginemos ahora que en el estudio que realizamos tan solo hemos podido reclutar los 18 primeros pacientes de la tabla 1. En este caso, los datos principales varían respecto a la muestra inicial de 50 casos (tabla 2).
La estimación del intervalo implicaría evaluar su error estándar y a continuación el IC95:
σm = σ/rn = 20,31/√18 = 4,79
IC95 = µ ± 2*σm = 146,94 ± 2*4,79 = (137,36 ; 156,51) mmHg
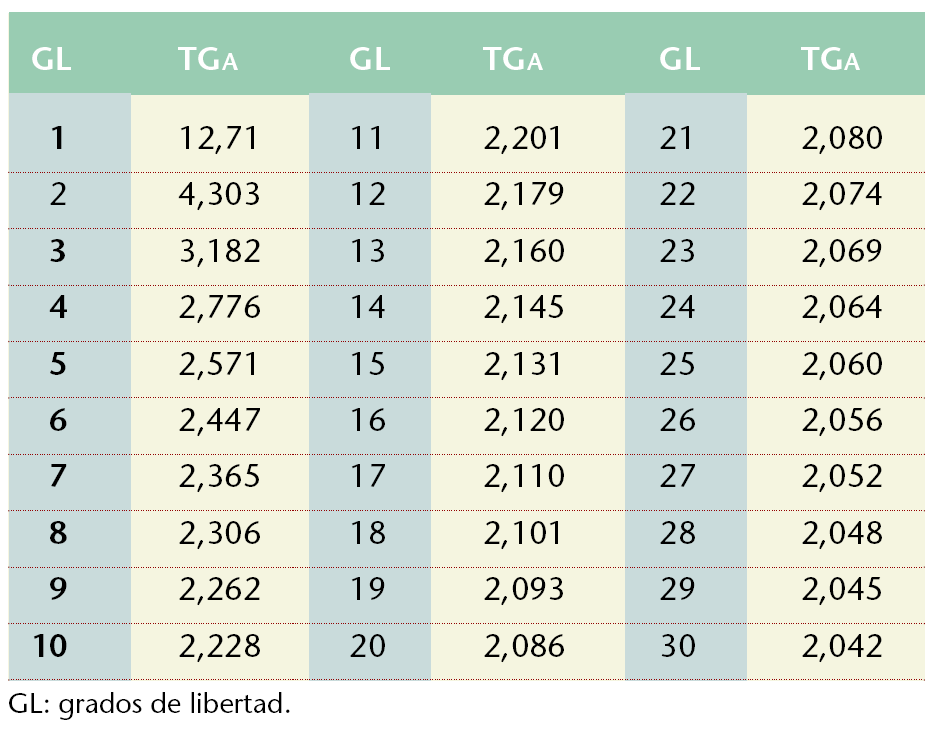
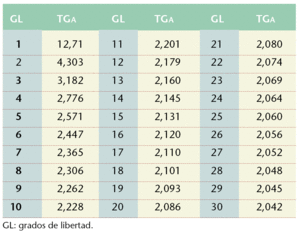
El valor de 2 que multiplica a σm (que no es más que una medida de posición relativa dentro de la distribución normal, denominado habitualmente como zα) se sustituye ahora por otro llamado tΓα, para el mismo grado de significación α (0,05), extraído en la tabla de distribución de la t de Student (tabla 3), quedando entonces como:
IC95 = µ ± tΓα*(σ/√n)
Teniendo en cuenta que existen (n-1) grados de libertad, siendo n el tamaño de la muestra, la tabla se utiliza buscando qué valor de tΓα se corresponde con los correspondientes grados de libertad. En nuestro caso hay 17 grados de libertad (: 18-1), correspondiéndole en la tabla un valor de tΓα igual a 2,110, por lo que finalmente queda:
IC95 = 146,94 ± 2,11*(20,31/®18) = (136,84 ; 157,04) mmHg
Obsérvese que cuanto más se aproxime el tamaño de la muestra a 30 sujetos, menor diferencia habrá entre el uso de uno u otro método, pero ello no quiere decir en ningún momento que el tamaño de muestra adecuado para un estudio sea de 30 individuos aproximadamente.
De la muestra a la población: intervalo para proporciones
Los datos de proporciones precisan también analizarse para estimar su intervalo de confianza. Siguiendo con el ejemplo de la tabla 1 se puede observar que hay 17 participantes que presentan una PAS por debajo de 140 mmHg, es decir, se observa una proporción (p) de 0,34 o 34% (:17/50) que presentan un control de su PAS mientras que 0,66 o 66% (:1,00-0,34) no la controlan.
Siempre que se cumpla que [n*p]≥5 y que [n*(1-p)]≥5, con el mismo argumento que se planteó para pasar de la muestra a la población diana en el caso de medias aritméticas, se procede a la estimación previa del error estándar (σp) de esta proporción:
σp = √ [(p*(1-p))/n] = √ [(0,34*(1-0,34))/50] = 0,067
Calculando a continuación el IC95 de la proporción p:
IC95 = p ± 2*σp
De esta forma, dado que [50*0,34]=17≥5 y que [50*(1-0,34)]=33≥5, el error estándar de la proporción de pacientes que presentan un adecuado control de la PAS es:
σp = √ [(0,34*(1-0,34))/50] = 0,067
Por tanto, el intervalo de confianza, con una significación del 95%, se estima entonces como:
IC95 = 0,34 ± 2*0,067 = (20,60 ; 47,40) %