A diferencia de lo expuesto previamente, la mayor parte de los datos en una investigación se corresponde con variables que podemos expresar con un número, es decir, variables cuantitativas. Ahora bien, éstos no podrán medirse con las escalas de medida que se expusieron, sino que precisan de otras diferentes.
Después de su medida y una vez que se dispone de un conjunto de valores de variables cuantitativas, es preciso agruparlos en unos índices o estadísticos que permitan su manejo.
Escalas de medida de las variables cuantitativas
Para el caso de variables cuantitativas, las escalas de medida difieren sensiblemente de las vistas con anterioridad. En este caso hay dos tipos de escalas: de intervalo y de razón.
Escala de intervalo
Incorpora las cualidades de las anteriores y, además, establece que existe la misma diferencia entre cada valor. Asimismo, carece de cero absoluto, puesto que el cero es arbitrario y puede incluso adoptar valores negativos. Ejemplo de ello es la diferencia entre la estimación de su estado de salud de 0,9 y 0,8, que es la misma que de 0,6 y 0,5. Además, el cero sería un valor indicado de forma arbitraria que no significa la falta absoluta de salud.
Escala de razón
Es la más perfeccionada, pues toma todas las características de todas las escalas e incorpora el cero absoluto; es decir, el cero tiene un sentido real. Así, el valor de la presión arterial sistólica de 150 mmHg presenta la misma superioridad sobre el de 140 mmHg que el de 120 sobre 110 mmHg, además de ser mayor y estimarse que 0 mmHg significa la ausencia total de presión arterial.
De acuerdo con lo expuesto, con las escalas de intervalo se pueden restar valores y con las de razón se pueden también dividir.
Manejo de variables cuantitativas
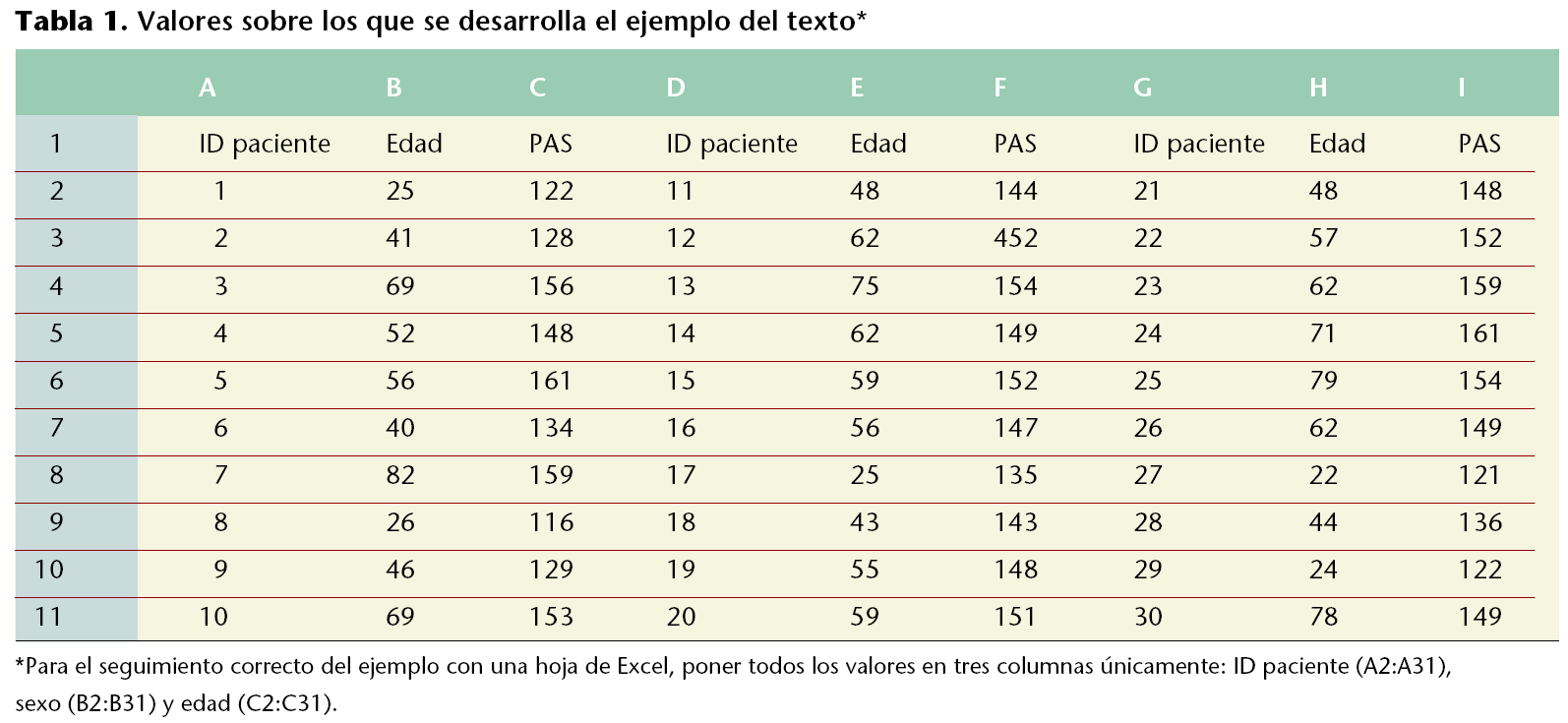
Para una mejor comprensión del manejo de estas variables, se utilizarán los datos de la tabla 1 (de Excel), que ofrece los datos obtenidos para las variables edad y presión arterial sistólica (PAS).
Estadísticos
Los valores de la tabla 1 ofrecen poca o nula información acerca de la edad de los pacientes, así como de su presión arterial, pues comprenden una gran cantidad de números que no se pueden manejar. De este modo, es preciso disponer previamente de unos índices que agrupen la información de cada variable cuantitativa. Éstos son los llamados estadísticos, que se obtienen después de efectuar unos determinados cálculos aritméticos sobre el conjunto de valores de la muestra de pacientes. Si estas operaciones matemáticas se efectuaran sobre los valores de toda la población, los índices así obtenidos se llamarían parámetros.
De este modo, la primera actuación en el manejo de las variables cuantitativas corresponde a la obtención de unos índices que entreguen información del valor del punto central o medio de todo el conjunto de valores, así como otros índices que informen acerca de cómo se desvían los valores de este punto medio. Los primeros corresponden a las medidas de centralización y los segundos a las de dispersión. Finalmente, otro tipo de medidas, las de localización, ofrecen información acerca de la ubicación de los elementos de la muestra en el conjunto.
Medidas de tendencia central
Tres son los estadísticos o índices empleados habitualmente en la descripción de los valores de una muestra: la media aritmética, la mediana y la moda.
Media aritmética
Es el valor promedio del conjunto de datos de la variable. Se representa habitualmente como (m). En Excel se calcula mediante la función PROMEDIO y en el ejemplo de la tabla anterior se corresponde con 53,23 para edad [=PROMEDIO(B2:B31)] y 144,40 para PAS [=PROMEDIO(C2:C31)].
Mediana
Es el valor del dato intermedio cuando se ordenan de mayor a menor todos los valores. Se representa normalmente como (Md) y se calcula en Excel mediante la función MEDIANA; en el ejemplo desarrollado es de 56 para edad [=MEDIANA(B2:B31)] y 148,5 para PAS [=MEDIANA(C2:C31)].
Moda
Se corresponde con el valor que se presenta con mayor frecuencia. Se representa corrientemente como Mo. En Excel se estima con la función MODA y ofrece unos valores de 62 para edad [=MODA(B2:B31)] y de 148 para PAS [=MODA(C2:C31)].
Medidas de dispersión
Cuando se ha descrito que la media de edad es de 53,23 años, se observa que en la muestra del ejemplo hay pacientes que tienen una edad bastante diferente, por lo que este índice no ofrece una información exacta de la muestra. Para completar la información se precisa de unos índices que muestren cuán dispersos están todos los datos respecto de esta medida central. Entre los estadísticos más utilizados se hallan:
Máximo, mínimo y amplitud
El máximo y mínimo dan idea de los valores extremos del conjunto; se calculan en Excel mediante las funciones MAX, MIN mostrando los valores de 82 años [=MAX(B2:B31)] y 161 mmHg [=MAX(C2:C31)] para el máximo y 22 [=MIN(B2:B31)] y 116 [=MIN(C2:C31)] para el mínimo. La amplitud o rango es la diferencia entre el máximo y el mínimo: 60 años y 45 mmHg.
Desviación típica o estándar y varianza
La desviación típica o estándar, representado por S, evalúa el error cometido cuando se indica como valor de la variable el de su media. Se calcula en Excel mediante la función DESVEST, y ofrece los valores de 17,21 años [=DESVEST(B2:B31)] y 12,90 mmHg [=DESVEST(C2:C31)].
La varianza se representa como S2, ya que es el cuadrado de la desviación típica; se estima en Excel mediante la función VAR, y ofrece los valores de 296,12 años [=VAR(B2:B31)] y 166,52 mmHg [=VAR(C2:C31)].
Otros datos estadísticos de menor relevancia son el coeficiente de variación de Pearson (cociente entre desviación típica y la media), que permite comparar desviaciones entre dos muestras; los coeficientes de curtosis, que informan acerca del apuntamiento de la distribución de valores, y los coeficientes de asimetría, que indica la existencia de sesgos. Estos coeficientes se pueden estimar con Excel mediante las funciones CURTOSIS y COEFICIENTE.ASIMETRÍA, respectivamente.
Medidas de localización
Estas medidas dividen la muestra en varias partes iguales, por lo que pueden clasificar después cada elemento en una ubicación concreta. En función del número de partes en que se divida se obtienen cuarteles (en 4 partes), deciles (en 10) o presentiles (en 100).
Excel permite calcular estos estadísticos. Así, los cuarteles se estiman mediante la función CUARTEL y los presentiles con la función PERCENTIL; con esta última función se pueden estimar todos los demás teniendo en cuenta que el cuartil 1, 2, 3 y 4 se corresponde con el percentil 0,25, 0,50, 0,75 y 1, respectivamente, y que el decil 1, 2, 3,... se corresponde con el percentil 0,1, 0,2, 0,3,... respectivamente.
De este modo, los valores de los percentiles más utilizados son:
• Para la edad, P25: 43,25 años [=PERCENTIL(B2:B31;0,25)], P50: 56 años [=PERCENTIL(B2:B31;0,5)] y P75: 62 años [=PERCENTIL(B2:B31;0,75)].
• Para la PAS, P25: 135,25 mmHg [=PERCENTIL(C2:C31;0,25)], P50: 148,5 mmHg [=PERCENTIL(C2:C31;0,5)] y P75: 152,75 mmHg [=PERCENTIL(C2:C31;0,75)].
Resumen de estadística descriptiva en Excel
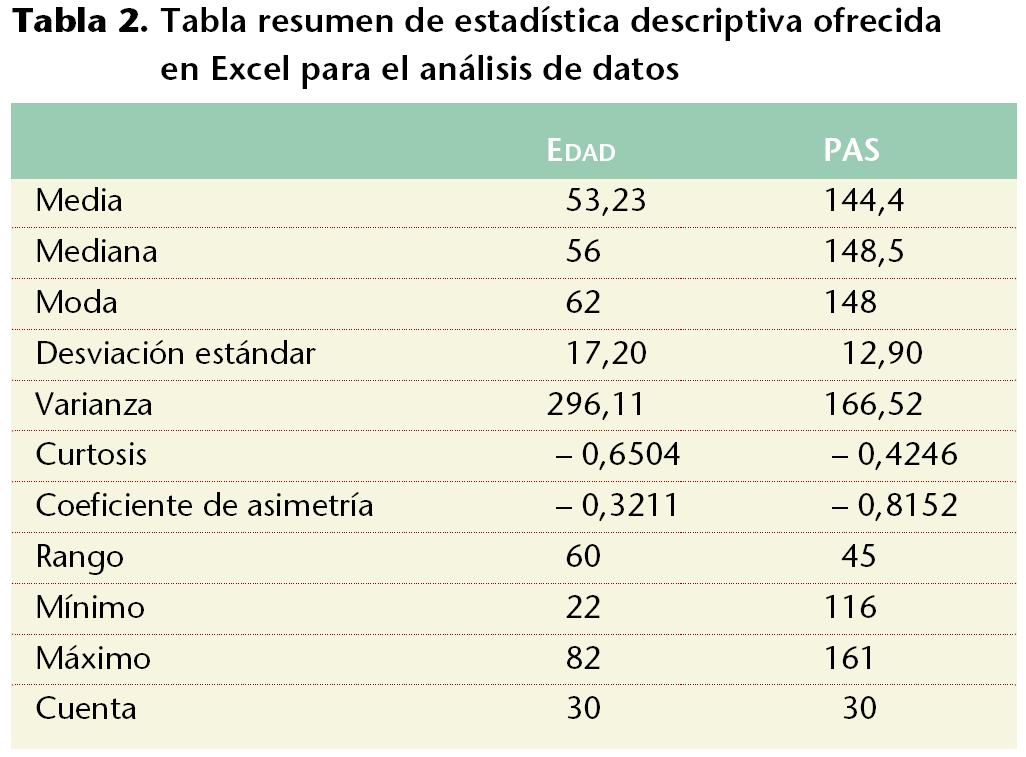
Finalmente, Excel permite la obtención de todos los estadísticos principales reunidos mediante la función ESTADÍSTICA descriptiva que se ubica en el módulo ANÁLISIS DE LOS DATOS DE HERRAMIENTAS. En nuestro ejemplo, la aplicación de esta función ofrece los valores de la tabla 2, donde se obtiene una información detallada de la muestra que se está analizando.
PDF
Consultora cientÍfica