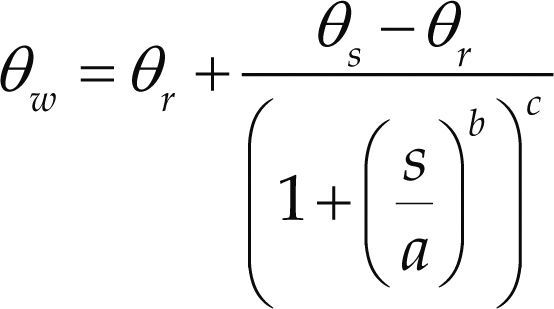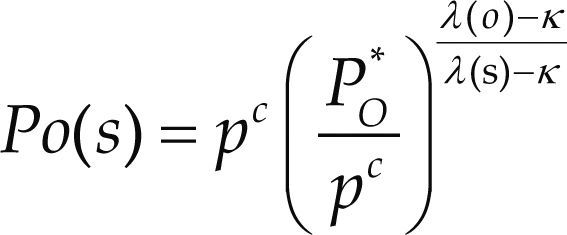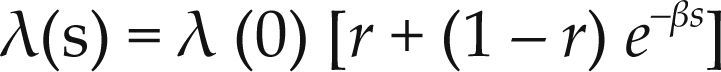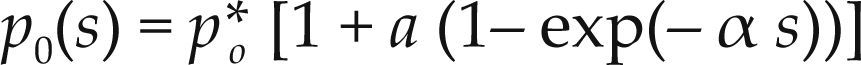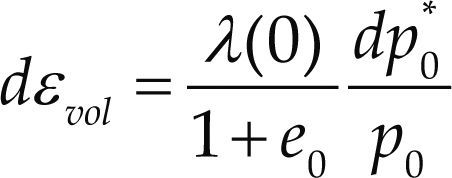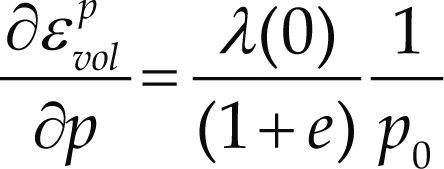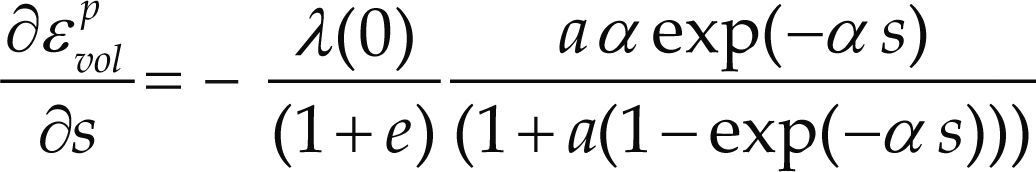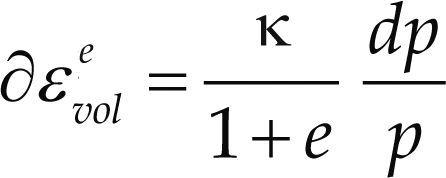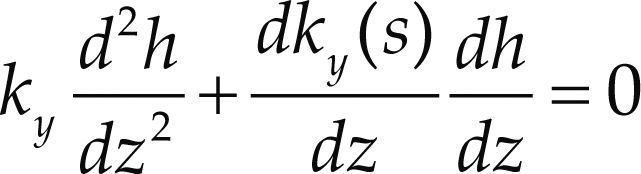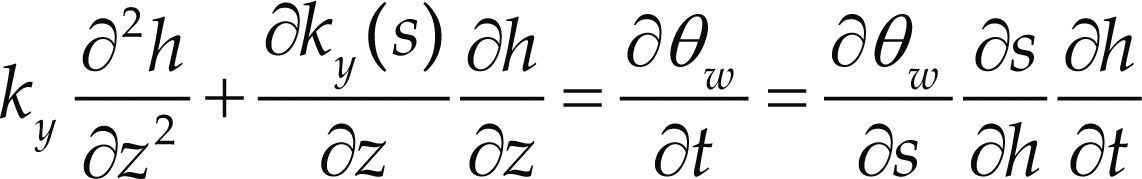El comportamiento de los suelos compactados depende de su densidad seca máxima y de su contenido de agua. Los terraplenes de carretera deben diseñarse para tener deformaciones tolerables producidas por peso propio, solicitaciones externas y variación volumétrica producida por los cambios de contenido de agua. En el caso de los suelos de baja plasticidad, los cambios de humedad producen deformaciones por colapso cuando se humedecen, esta deformación se acentúa en suelos poco compactados. Como los suelos compactados están parcialmente saturados, es conveniente estudiar su estabilidad volumétrica, tomando en cuenta los conceptos propios de la mecánica de suelos parcialmente saturados como: la curva de retención, la variación de la permeabilidad, el flujo de agua y el clima de la zona. Con base en lo anterior, es posible establecer si el grado de compactación y el contenido de agua es el adecuado para los fines de diseño. En este trabajo se presentan los resultados de un análisis aplicado a un terraplén representativo de la autopista Pátzcuaro-Uruapan, en el que se cuantificó la infiltración del agua en el tiempo y se utilizó el Modelo Básico de Barcelona para el cálculo de las deformaciones de colapso. Se observó que existe un problema de bajo grado de compactación de suelo, el cual origina deformaciones de colapso de hasta 48cm en un terraplén con altura de 15 m en un periodo de tres años.
The behavior of compacted soil depends on its maximum dry density and water content. The embankments of roads must be designed to have tolerable deformations caused by their own weight, external stresses and volume changes produced by water content change. In the case of low plasticity soils the changes in humidity cause collapsing deformations, these deformations are accentuated in loose soils. As compacted soils are partially saturated soils, it is advisable to study the volumetric soil stability considering particular concepts of partially saturated soils such as the retention curve, the variation in permeability, the water flow and local climate. Based on the above concepts it is possible to determine, if the degree of compaction and the water content is suitable for design purposes. The results of an analysis of a typical embankment representative of the Pátzcuaro-Uruapan highway are presented in this work, water infiltration was quantified over time using the Barcelona Basic Model to estimate collapsing deformations. It was noted that there is a problem of low compacting soil degree, which causes collapse up to 48cm in an embankment of 15 m high over a period of three years.
Las obras de infraestructura carretera se pueden considerar como una serie de estructuras que soportan el pavimento flexible por donde transitan los vehículos, se forman principalmente por estructuras de tierra construidas a partir de materiales sueltos sometidos a compactación para conseguir una estructura resistente y poco deformable.
Los terraplenes son estructuras más comunes en las carreteras sobre todo en terrenos de lomerío o montañoso, frecuente en autopistas debido a las especificaciones de baja pendiente de estas obras. Las deformaciones excesivas de estos elementos estructurales llevan a cuantiosos gastos de mantenimiento en los pavimentos. En el estado de Michoacán se presenta el caso de la autopista Pátzcuaro-Uruapan, en cuyos terraplenes se forma un pequeño columpio que desaparece en la zona de corte. La principal causa de las deformaciones es el colapso por humedecimiento, aunque pueden existir otras muy importantes como la erosión interna que posteriormente lleva a un colapso interno.
El estudio de los suelos compactados involucra el estudio la variación de la energía de compactación y el contenido de humedad para obtener las propiedades mecánicas deseadas del suelo en este tipo de obras. En el caso de los terraplenes se requiere que el suelo sea poco compresible, con una resistencia alta, además de ser poco susceptible al colapso por humedecimiento. Lo deseable es que se realice un estudio en laboratorio para estimar las condiciones y el tipo de suelo que cumplirá con las propiedades mecánicas especificas en el proyecto y, por otro lado, que se determinen las condiciones de compactación en campo para alcanzar estas propiedades (Mendoza, 1992). Es decir, la gran variedad de suelos que existen no se pueden compactar con las mismas especificaciones, deben corroborarse las propiedades mecánicas en laboratorio para aplicarlas en campo.
Una vez en campo, el suelo compactado se somete a las variaciones de humedad propias de la zona geográfica en las que se encuentra y el suelo se adapta a estas condiciones dependiendo de su contenido inicial de humedad y de su grado de compactación. Si el suelo está demasiado seco para las condiciones de humedad del sitio, se humedecerá, provocándose una lubricación entre las partículas que producirá un asentamiento del suelo bajo su propio peso (Alonso et al., 2010). Entonces, las condiciones iniciales de compactación son importantes para determinar el comportamiento de colapso por humedecimiento, además de la densidad inicial del suelo, donde la microestructura del suelo compactado juega un papel muy importante (Alonso et al., 2013).
El objetivo del presente trabajo es estudiar el comportamiento mecánico de un limo compactado característico de la región nororiente del estado de Michoacán, para explicar las deformaciones en algunos de los terraplenes de la autopista Pátzcuaro-Uruapan. En la figura 1 se presentan fotografías donde se observan las ondulaciones del pavimento (zonas de terraplén), debidas a asentamientos de colapso por humedecimiento, que fue tema de la hipótesis que originó el presente estudio. Además se realizó una caracterización del limo en laboratorio, basada en los conceptos de la mecánica de suelos parcialmente saturados. A su vez, se calibra el Modelo elasto-plástico Básico de Barcelona (BBM), con el que se simula el comportamiento de colapso de terraplenes sometidos a infiltración provocada por las lluvias de la zona, obteniendo las conclusiones pertinentes.
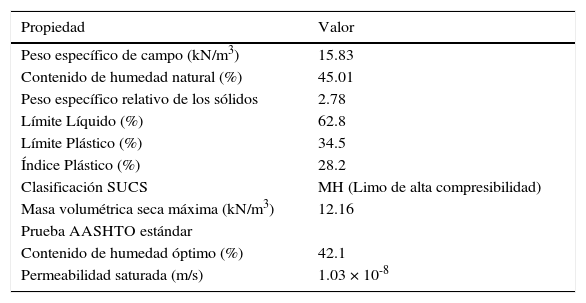
Pruebas realizadasEl material se muestreó de los taludes de corte de la autopista Pátzcuaro-Uruapan en el km 51+000. Se practicaron ensayos de rutina necesarios para su clasificación e identificación. Los resultados se resumen en la tabla 1. El suelo es un limo de alta compresibilidad, con un límite líquido mayor a 50%, que es el máximo que marca la norma para terraplén (N CMT 1 01/02). Se realizó la prueba de compactación AASHTO estándar, de donde se obtuvo una masa volumétrica máxima de 12.16kN/m3 y un contenido de humedad óptimo de 42.1%, por otro lado, se estimó la permeabilidad saturada de una prueba de consolidación.
Propiedades principales del suelo en estudio
| Propiedad | Valor |
|---|---|
| Peso específico de campo (kN/m3) | 15.83 |
| Contenido de humedad natural (%) | 45.01 |
| Peso específico relativo de los sólidos | 2.78 |
| Límite Líquido (%) | 62.8 |
| Límite Plástico (%) | 34.5 |
| Índice Plástico (%) | 28.2 |
| Clasificación SUCS | MH (Limo de alta compresibilidad) |
| Masa volumétrica seca máxima (kN/m3) | 12.16 |
| Prueba AASHTO estándar | |
| Contenido de humedad óptimo (%) | 42.1 |
| Permeabilidad saturada (m/s) | 1.03 × 10-8 |
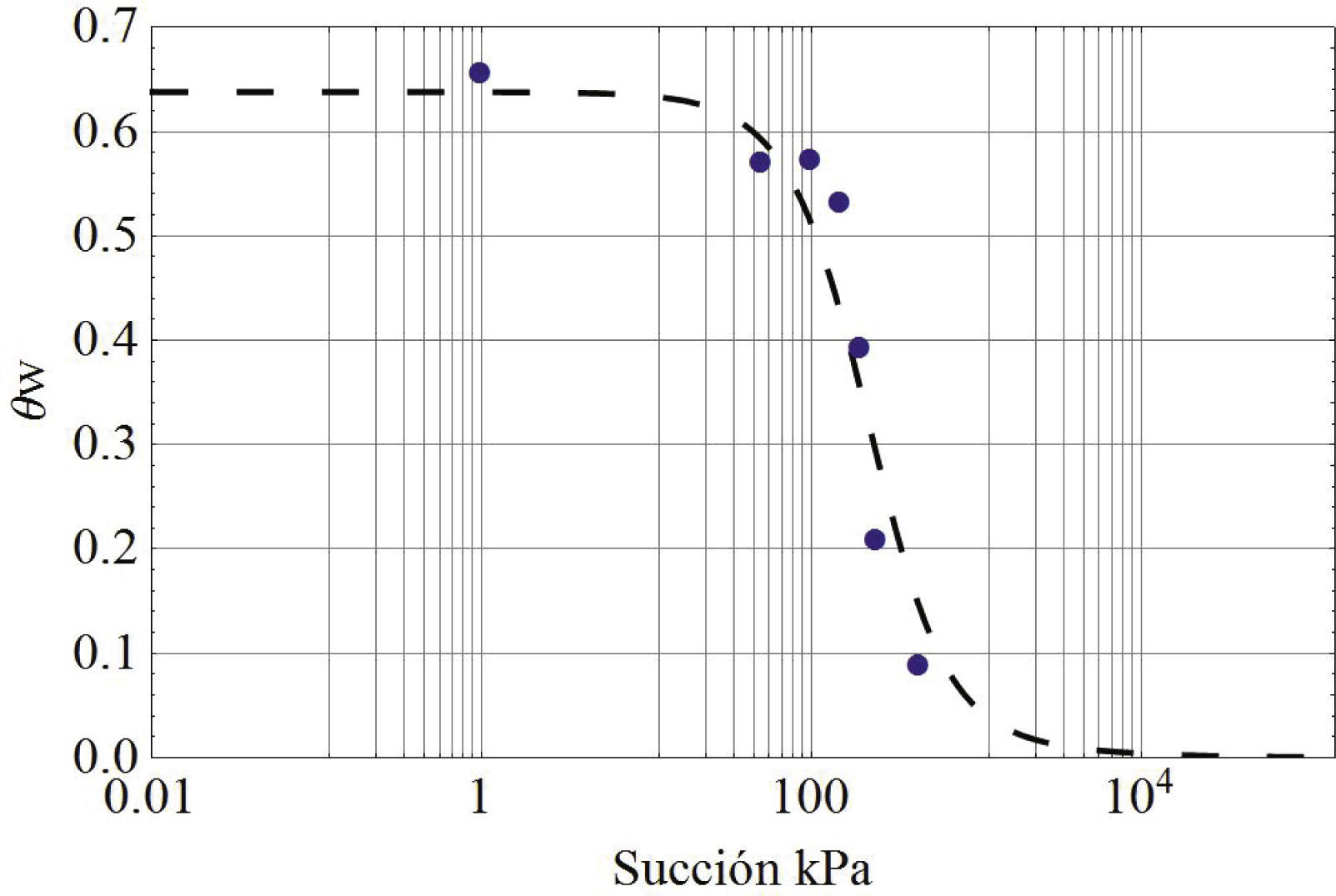
Se realizaron adicionalmente ensayos propios de suelos parcialmente saturados con un consolidómetro con control de succión, para obtener la curva característica o de retención del suelo. En este caso se impuso una succión aplicándose una presión de aire a la muestra en la parte superior y se instaló un disco de alto valor de entrada de aire en la parte inferior de la muestra para evitar la desaturación. Se aplicó una pequeña carga en la parte superior para asegurar el contacto entre pistón del consolidómetro y la muestra de suelo. La muestra se montó con el contenido de humedad óptimo y densidad que corresponde a 90% del grado de compactación, se procedió a saturar permitiendo la expansión, que fue baja, posteriormente se aplicó presión de aire en etapas (distintas succiones), después se midió el agua desalojada para cada etapa por la parte inferior de la muestra con una bureta. En la figura 2 se presentan los puntos experimentales obtenidos, estos valores se ajustaron con el Modelo de Van Genuchten (1980), que se representa en la ecuación (1)
donde
θw = contenido volumétrico de agua con una succión “s”
θs = contenido volumétrico de agua del suelo saturado
θr = contenido volumétrico de agua residual
a,b,c = parámetros del modelo
Los valores de los parámetros después del ajuste de la ecuación (1) resultaron θs=0.62, θr= 0.001, a=189, b=5.42 y c=0.47. Alternativamente se pueden utilizar relaciones empíricas para obtener los parámetros de la curva de retención, por ejemplo, los que se presentan en la nueva guía AASHTO de diseño de pavimentos, donde se correlaciona el porcentaje que pasa la malla Núm. 200, multiplicado por el índice plástico con los parámetros de ajuste para el modelo de Fredlund y Xing (1994).
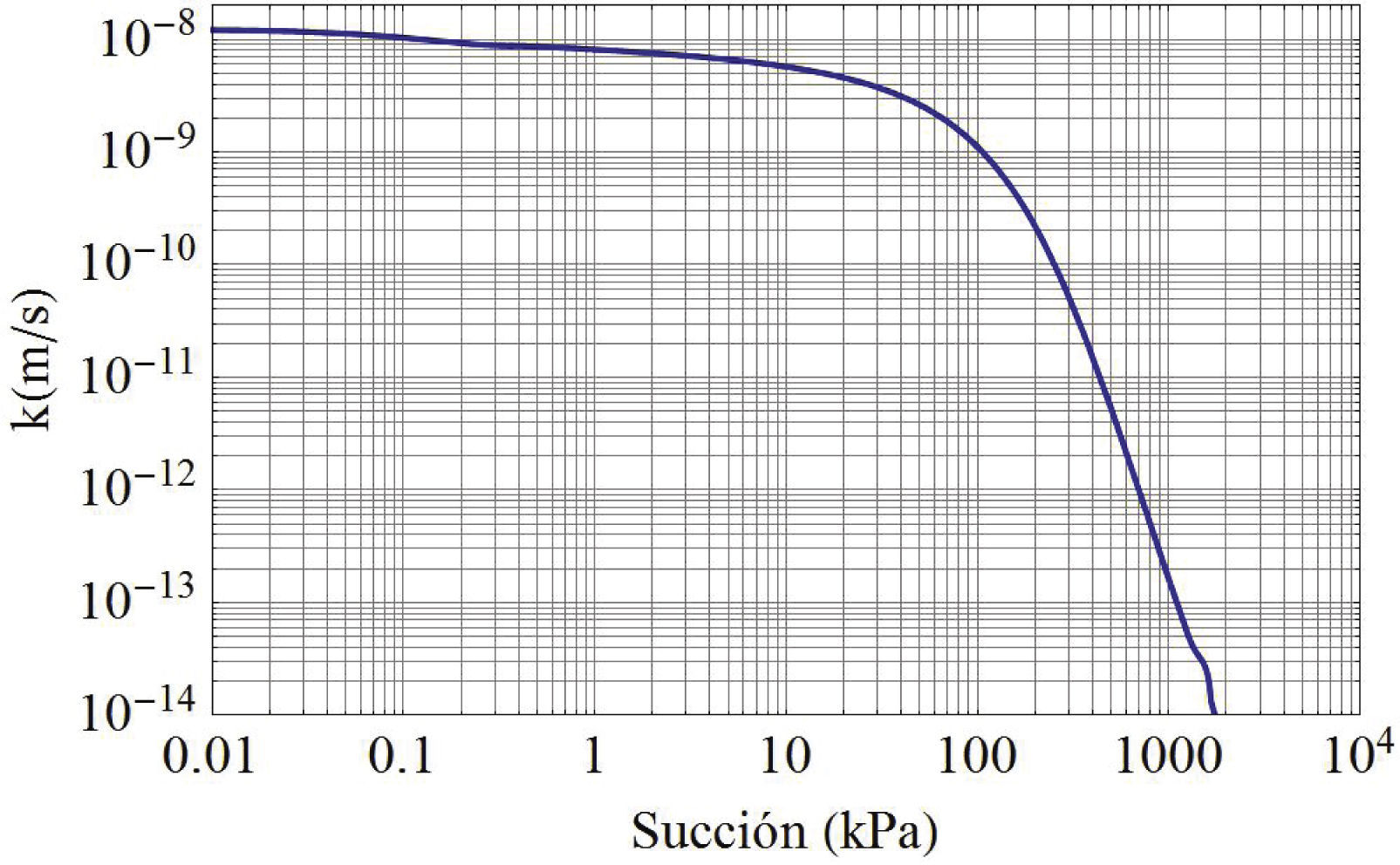
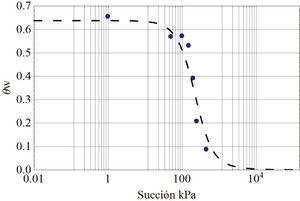
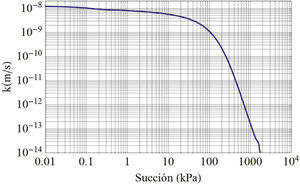
La curva de conductividad hidráulica se estimó por el método de Fredlund et al., (1994) (figura 3), para ello se usó la curva característica medida (figura 2) y la conductividad hidráulica saturada que se determinó indirectamente mediante la prueba de consolidación del suelo saturado. La muestra que se utilizó para obtener la permeabilidad saturada se reconstituyó al grado de compactación de 90% y con un contenido de agua óptimo de la prueba AASHTO estándar de 42%; valores recomendados por la normativa mexicana para terraplenes antes mencionada.
Curva de conductividad hidráulica del suelo estimada mediante el modelo de Fredlund et al. (1994)
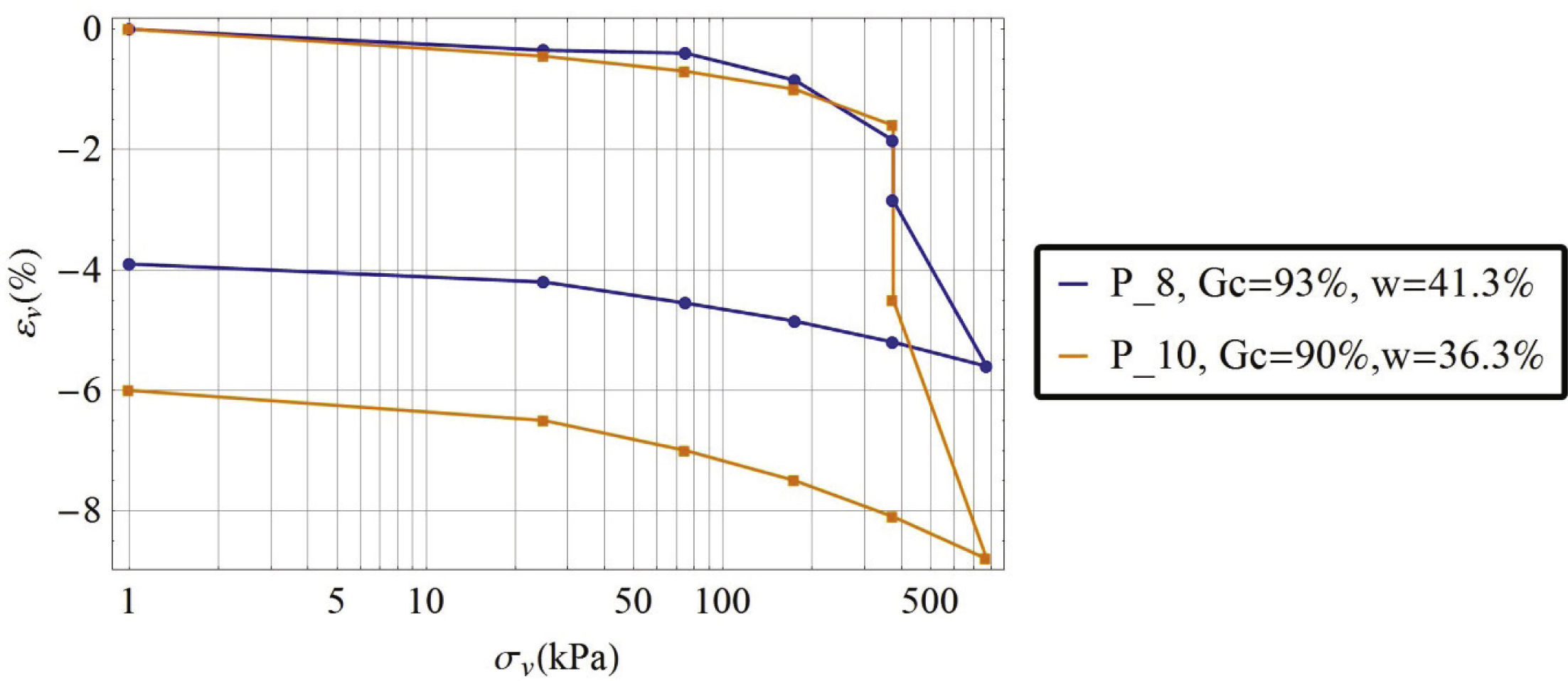
Una de las etapas de este trabajo fue reproducir muestras reconstituidas a grados de compactación similares a los del suelo en el campo, de acuerdo con la norma SCT. Además, se realizaron ensayos para determinar el potencial de colapso que tiene el suelo, sometiendo la muestra al colapso por humedecimiento; los ensayos se realizaron en un equipo convencional de consolidación, con brazo de palanca, pesas para la aplicación de esfuerzo y sin control de succión. En los ensayos se procuró mantener constante el contenido de agua, antes de la saturación, no permitiendo la salida del agua por los discos porosos; este es un tipo especial de ensayo en suelos parcialmente saturados.
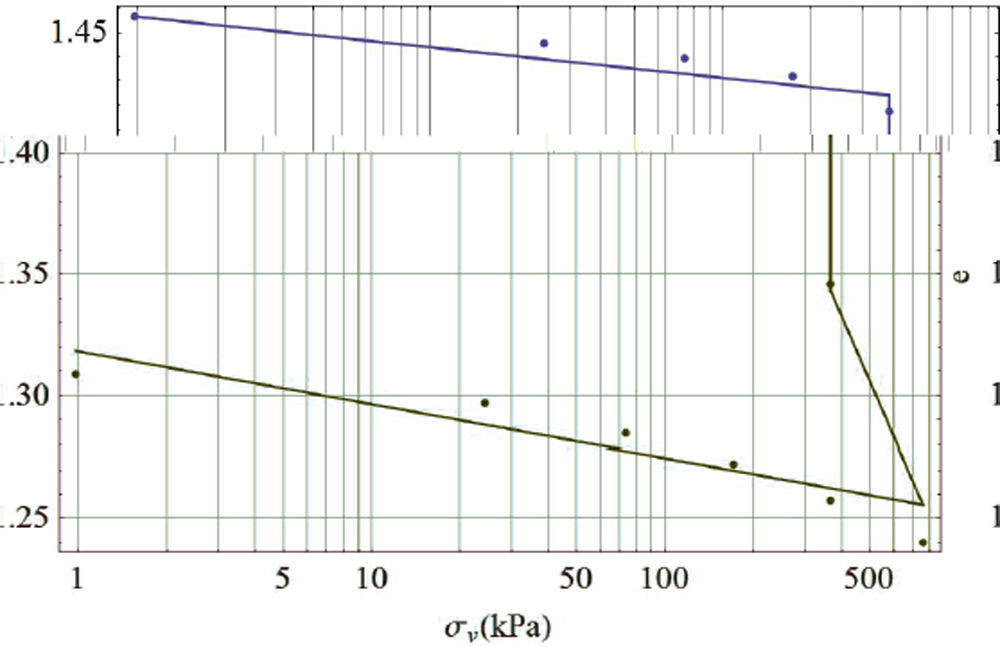
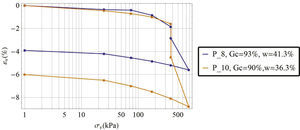
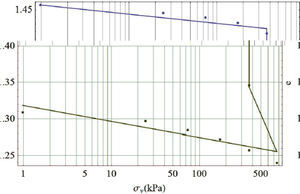
La figura 4 muestra los resultados de dos pruebas de consolidación, una con un grado de compactación de 93% (ensayo P_8) y la segunda con un grado de compactación de 90% (ensayo P_10). Ambos ensayos se saturaron a un esfuerzo vertical constante σr = 375kPa para producir el colapso por humedecimiento y posteriormente se terminaron los ensayos en condiciones saturadas. El potencial de colapso (ASTM D 5333-03) que se obtuvo del ensayo P_10 fue de 2.9% y para el ensayo P_8 fue de 1%. La normativa mexicana no marca restricciones en cuanto el colapso por humedecimiento, por otro lado, la normativa Española (PG-3, 2002) considera que los suelos colapsables son aquellos que sufren una deformación superior a 1% cuando se humedecen, compactándolos a la densidad máxima del ensayo Proctor normal; desde este punto de vista, el suelo en estudio no es colapsable, ya que a 93% de grado de compactación colapsa 1%. El problema radica en que para terraplenes en México, el suelo suele compactarse a 90± 2% (N CMT 1 01/02), es decir, la compactación no es suficiente para limitar el colapso por humedecimiento y no se realiza un estudio con el suelo compactado para limitar este tipo deformaciones. Rico et al. (1990) recomienda que el grado de compactación sea de 95 y 95±2% para el caso de los terraplenes de obras tipo I (autopistas y red federal) para suelos de calidad deseable y adecuada, respectivamente; valores que serían suficientes para limitar la deformación de colapso por humedecimiento del suelo en estudio.
Modelación matemáticaEn esta sección se describe una opción de cómo realizar el cálculo de las deformaciones de colapso por humedecimiento, tomando como base la información que se obtuvo de pruebas de consolidación en laboratorio sobre suelos parcialmente saturados.
Breve descripción del Modelo Básico de Barcelona (BBM)El modelo constitutivo básico de Barcelona, mejor conocido por su acrónimo en inglés como BBM (Barcelona Basic Model), desarrollado por Alonso et al. (1990) es un modelo elasto-plástico que se utiliza para describir el comportamiento esfuerzo-deformación de suelos parcialmente saturados. Este modelo tiene un rango de aplicabilidad a suelos poco o moderadamente expansivos y se pueden modelar dos tipos de trayectorias de esfuerzo: trayectorias de compresibilidad a succión constante y trayectorias de colapso por humedecimiento.
El modelo está formulado en términos de dos esfuerzos independientes: el esfuerzo medio neto, que es igual al esfuerzo total medio (pm= (σ1+ 2σ3)/3) menos la presión de aire, es decir, p = pm– ua, y la succión matricial o capilar “s”, que es igual a la diferencia de la presión de aire y agua (s = ua– uw).
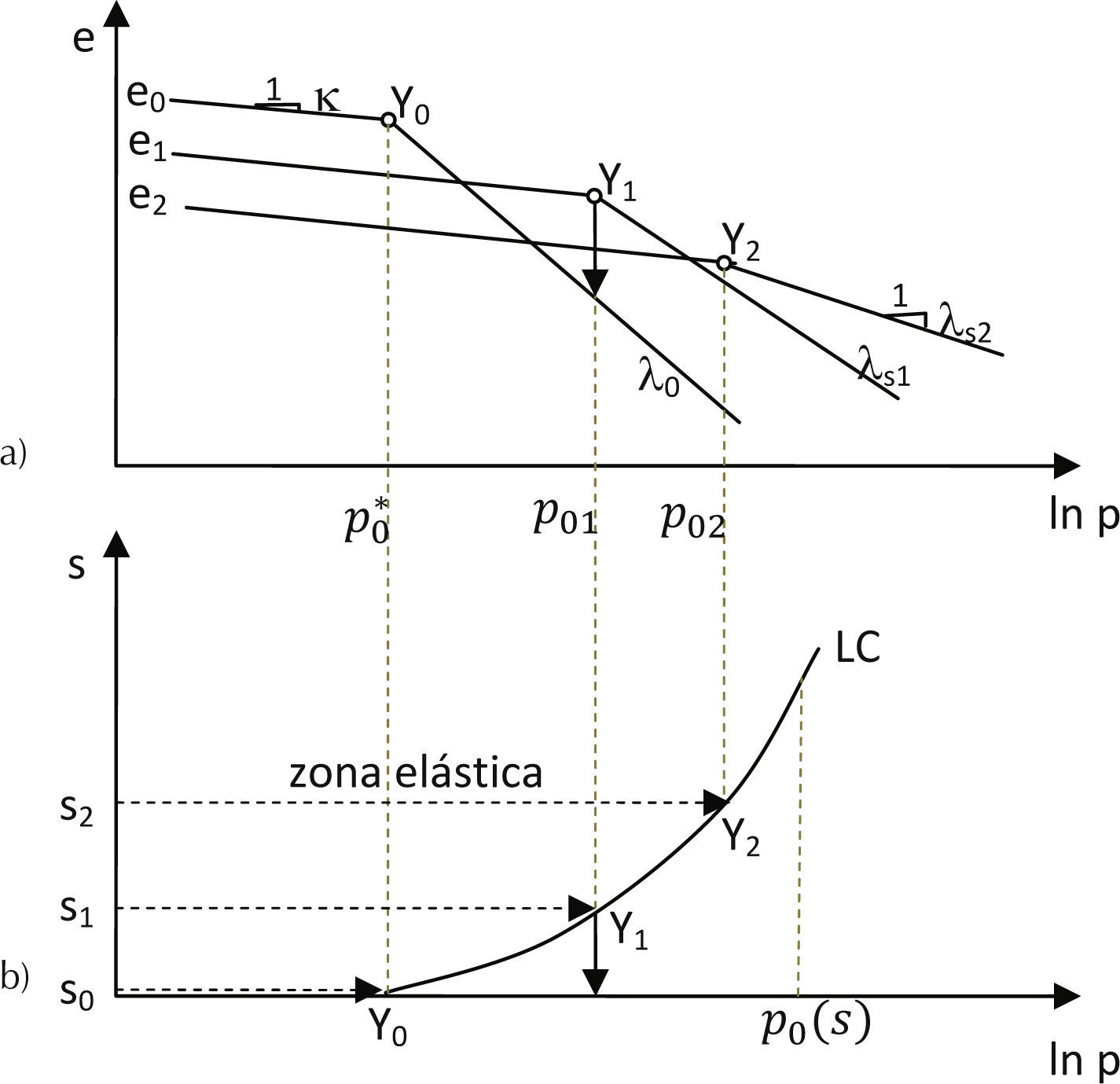
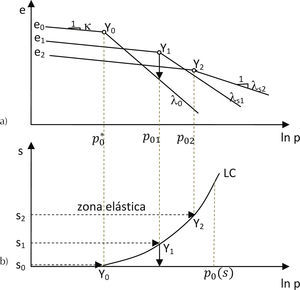
La base del modelo de BBM es la curva de compresibilidad de un suelo saturado con trayectoria isótropa, “s0” (figura 5b). La curva de compresibilidad (figura 5a) tiene un punto de fluencia Y0 a un esfuerzo de referencia p0*, hacia la derecha se producen deformaciones plásticas no recuperables y si se descarga se regresa a la zona elástica. En una trayectoria a una succión mayor, “s2”, tiene una reducción en su relación de vacíos inicial por el incremento de la succión y un punto de fluencia, ϒ1, a un esfuerzo p01 mayor que el anterior; en una trayectoria de succión “s3” pasa algo similar a lo anterior. Se hace notar que a medida que la succión aumenta la pendiente de la curva de compresibilidad (λs) en su zona virgen disminuye, esto es función de la succión. En las Figuras 5a y b se proyectan los puntos de fluencia ϒ, y a la curva que se forma con la unión de estos puntos, en el plano de succión contra el ln p, se le denomina LC (Loading-Collapse); que se define como el lugar geométrico de los esfuerzos medios de preconsolidación para succión variable. A la curva LC la pueden interceptar trayectorias de cambio de esfuerzo a succión constante (como las anteriormente descritas) o trayectorias de cambio de succión a esfuerzo medio neto constante, con las que puede predecir el colapso por humedecimiento como la que se presenta en el esfuerzo de fluencia Y1 (figura 5a).
a) curva de compresibilidad del suelo; b) puntos y curva de fluencia LC (Alonso et al., 2010)
La curva LC se define por la ecuación (2) (Alonso et al., 1990)
donde:
po(s) = esfuerzo neto de preconsolidación para una suc ción cualquiera s
Po* = esfuerzo neto medio de consolidación en condiciones saturadas po*=po0
λ (0) = índice de compresión de la curva virgen de consolidación para condiciones saturadas
λ(s) = índice de compresión a succión constante s
κ = índice de compresión elástico
pc = esfuerzo medio de referencia.
El valor de λ(s) se determina por la expresión empírica de la ecuación (3), es decir, la pendiente de la curva de compresibilidad depende de la succión a la que se encuentre el suelo.
Dónde r y β son parámetros del modelo.
Alternativamente se puede utilizar la ecuación (4) para la curva LC (Alonso et al., 2010)
En esta ecuación intervienen, el parámetro “a”, el cual proporciona el valor límite de p0(s) para un incremento infinito en la succión; y α que controla el incremento de p0 respecto al incremento de “s”. En el presente trabajo se utiliza la ecuación (4) por simplicidad y además se mantiene constante la pendiente de la curva de compresibilidad, ya que se necesitan pruebas más elaboradas para obtener su variabilidad. Esta aproximación no causa demasiado error desde el punto de vista práctico para este caso, ya que se considera una succión inicial constante después de compactar, a esta le corresponde una pendiente inicial λ(si), después se inicia el humedecimiento y comienza el colapso; solo se tiene una trayectoria de colapso, tal como lo realiza Alonso et al. (2010).
Cuando el esfuerzo p0(s) quiere cruzar la superficie de fluencia, esta crece y se producen deformaciones plásticas que generan un endurecimiento en el suelo, este se controla a través del parámetro (esfuerzo de preconsolidación en estado saturado) y se relaciona con las deformaciones volumétricas totales por medio de una relación lineal logarítmica mostrada en la ecuación
El valor de p0 es idéntico al valor de p, ya que en el rango elasto-plástico siempre se encuentra en la superficie de fluencia. Las deformaciones plásticas totales se pueden escribir en función de los cambios de succión y cambios de esfuerzo neto, por medio de la ecuación (6)
Las ecuaciones (4) y (5) se utilizan para el cálculo de las deformaciones plásticas en la ecuación (6). Por lo que se puede demostrar que las deformaciones plásticas debidas a cambio de esfuerzo y cambio de succión se representan por las ecuaciones (7) y (8)
De las ecuaciones anteriores se puede obtener la deformación volumétrica total al integrar en el rango de variaciones de esfuerzo neto, p, y de succión, s.
Las deformaciones en el rango elástico se pueden calcular con la pendiente carga recarga, κ, y la ecuación (9)
Las condiciones iniciales (γd y w) de densidad y contenido de humedad de un suelo compactado, pueden relacionarse con su carga de preconsolidación en estado saturado, po*, y la succión, “s”, en términos del modelo BBM. Sin embargo, estos parámetros no incluyen la información de la micro-estructura que es importante para los suelos compactados (Alonso et al., 2013).
Obtención de los parámetros del modelo BBMCon los resultados del ensayo P_10 se ajustó el Modelo elasto-plástico BBM, y se obtuvieron los parámetros que se presentan en la tabla 2. La modelación del ensayo P_10 se muestra en la figura 6, donde se observa que el modelo se ajusta de manera adecuada al comportamiento que se presentó en el laboratorio.
Parámetros del modelo BBM, deducidos del ensayo P_10
| Coeficiente de compresibilidad (kPa-1) | λ(0) = 0.1208 |
|---|---|
| Índice de compresión elástico (kPa-1) | κ = 0.00944 |
| Esfuerzo de preconsolidación en estado saturado (kPa) | po*=125 |
| Parámetro de la curva LC | a = 6.2 |
| Parámetro de la curva LC | α = 1.24 |
| Relación de vacíos inicial | ei 1.4565 |
Uno de los problemas típicos de la Autopista Pátzcuaro-Uruapan es el asentamiento por humedecimiento, este problema ha provocado que se realicen renivelaciones de manera periódica. En esta sección se presenta la simulación realizada del cálculo de los asentamientos de colapso, para ello se hizo un análisis en dos partes: la primera el cálculo de la infiltración del agua, (se abordó de dos maneras, con flujo estable y con flujo transitorio), la segunda involucró el cálculo de los asentamientos en el tiempo que se tienen a medida que se presenta la infiltración del agua. En la realidad los dos eventos son simultáneos, es decir, a medida en que el agua penetra se presenta un colapso, que a su vez, cambia las propiedades del suelo. En este caso, el problema se soluciona como eventos separados y en una dimensión, simplificando el problema.
Cálculo de la infiltración del agua en el sueloEn el caso particular de un terraplén de carretera, el contenido inicial de agua después de la construcción depende del agua agregada en el proceso de compactación. El clima afecta considerablemente, ya que si el terraplén se construye en temporada de lluvias existirá exceso de humedad, y al contrario, si se construye en temporada de calor, donde existirá una tendencia a la evaporación y escasez de agua. Las condiciones anteriores pueden producir que el terraplén tenga un contenido de humedad inicial del lado húmedo o seco, respecto al contenido óptimo de compactación. El suelo compactado del lado húmedo del contenido óptimo, tiene un comportamiento diferente que el suelo del lado seco, en el lado seco el suelo tiende a colapsar cuando se humedece (Mendoza, 1992, Alonso et al., 2010). Después de la compactación el suelo del terraplén tenderá a un equilibrio, que depende de las condiciones climáticas del sitio, lo más probable es que el equilibrio sea dinámico y se convierta en una variación cíclica del contenido de humedad.
En la presente investigación se analizó solo el caso de infiltración y se parte de la ecuación de flujo en una sola dimensión como caso simplificado. Se puede hablar de flujo estable y flujo transitorio. El flujo estable es la formulación más sencilla, la ecuación que gobierna el flujo se encuentra en función de la carga hidráulica, h, y la permeabilidad que está en función de la succión, ky(s) (figura 3); en el caso de los suelos parcialmente saturados, se puede escribir como se muestra en la ecuación (10)
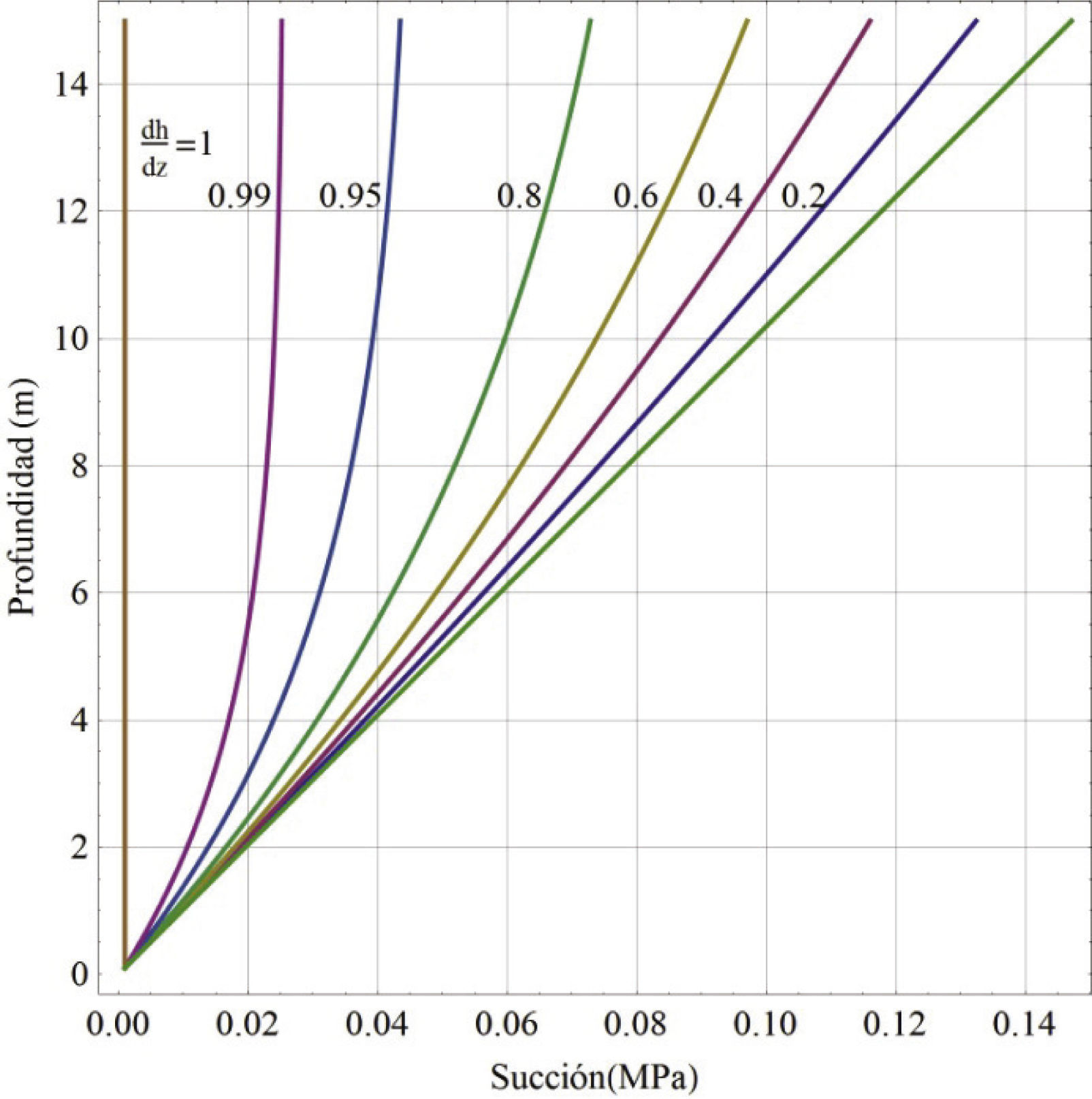
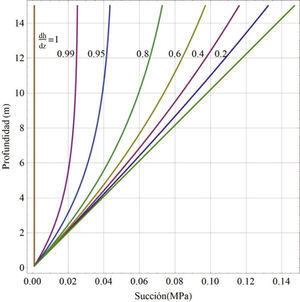
Si el agua se encuentra en un equilibrio estático, sin evaporación ni infiltración, la succión arriba del nivel de aguas freáticas tendrá un valor igual a z γw tomando en consideración que la presión de poro del aire es la atmosférica. En la figura 7 se presentan los resultados de un análisis para el caso donde se tiene el nivel de aguas freáticas a 15 m de profundidad, la línea verde inferior representa el nivel estático. La solución de la ecuación (10) es no lineal, debido a la variación de la permeabilidad respecto a la succión, para solucionar el problema supone una condición de contorno en la parte superior, donde el gradiente hidráulico es dh/dz = q / ksat= cte, la constante corresponde a la infiltración referida a la permeabilidad saturada. Se resuelve la ecuación (10) para la condición mencionada con valores de dh/dz igual a 0.2, 0.4, 0.6, 0.8, 0.95, 0.99 y 1; los resultados de los cálculos se grafican en la figura 7 para su análisis. Para que la succión se reduzca a cero es necesario que la infiltración se iguale a la permeabilidad saturada (q / ksat= 1), si la infiltración es menor, el suelo no se saturará. Debemos recordar que el análisis de flujo estable representa una condición de equilibrio después de un largo tiempo. La tasa de infiltración depende de la intensidad y frecuencia de la lluvia de la zona, además de la permeabilidad superficial de la cubierta (pavimento, vegetación, etcétera) y de la pendiente de la zona de infiltración. Por lo que se puede concluir que es complicado que el suelo se sature en un tiempo corto para el caso que se analiza (ksat = 8 × 10-4 m/día) y que para realizar un análisis apegado a la realidad debe hacerse un análisis de flujo transitorio.
En el caso de flujo transitorio para la fase del agua, se debe tomar el cambio de cantidad de agua en el suelo con respecto al tiempo, se suele utilizar el volumen de agua respecto al volumen del elemento, es decir, el contenido volumétrico del agua θw= Vw/ V0. Para un suelo parcialmente saturado, el contenido volumétrico del agua se encuentra en función de la succión, y se representa por la curva característica (figura 2). El flujo de agua a través de un elemento de suelo parcialmente saturado se puede calcular con base en la diferencia de agua que sale y entra (es decir, la ecuación(10)) que se iguala a la variación del volumen de agua en el tiempo. La variación del volumen en el tiempo se escribe en función de la carga hidráulica, como lo muestra la ecuación (11), a esta ecuación se le denomina: de Richards. En el presente trabajo se resuelve en una dimensión para el caso de infiltración.
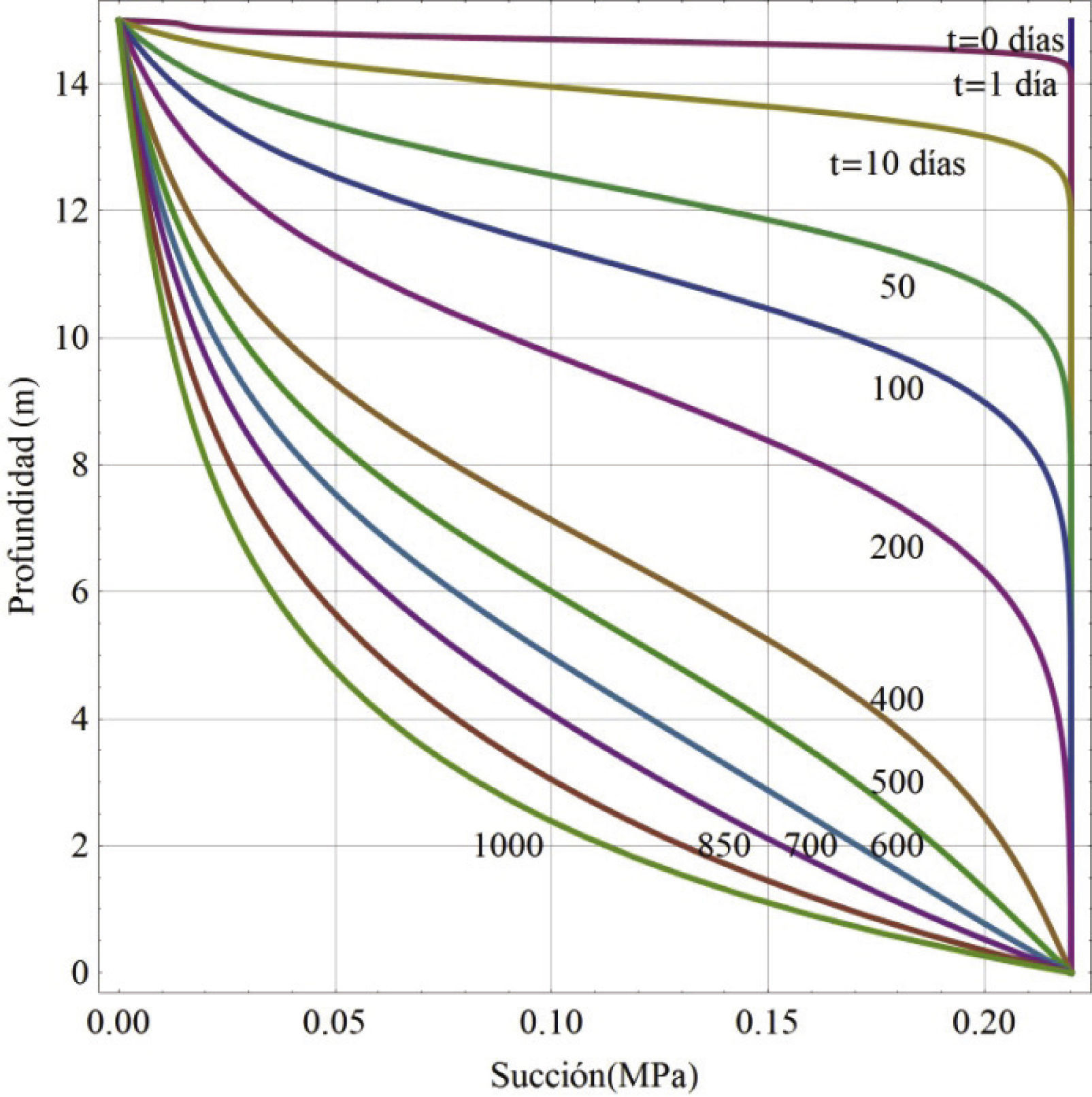
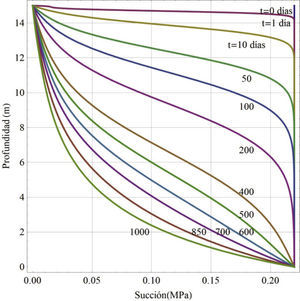
En el caso práctico se considera un terraplén que tiene una altura de 15 m, en este terraplén el agua se infiltra en la parte superior considerando un flujo en la dirección vertical. Se establecen condiciones de succión iniciales en el suelo, iguales en todo el espesor del terraplén, las cuales se pueden considerar con base en 90% de grado de compactación de la prueba AASHTO estándar (γd = 10.94kN / m3) y la humedad óptima de 42.1% (N CMT 1 01/02, características para terraplenes). Del suelo en estudio se puede deducir que, para la especificación de la Norma Mexicana (N CMT 1 01/02), el contenido volumétrico de agua es de 0.469 y con la curva de retención del suelo se puede obtener una succión inicial de 220kPa. Para este ejemplo se impone una carga hidráulica que corresponde a esta succión, igual en toda la altura de los 15 m. En la parte inferior (0 m), se mantiene constante la succión mencionada durante el proceso de infiltración. La solución del problema se muestra en la figura 8 para distintos tiempos, se puede apreciar cómo disminuye la succión a medida que pasa el tiempo, en el periodo de un año ya se tiene una disminución de la succión considerable.
Es evidente que en la realidad no se mantiene una infiltración por un tiempo prolongado, como ya se comentó, existen ciclos de humedecimiento y secado, aun en el periodo de lluvias. Por lo que estos cambios de humedad serán paulatinos y se darán con mayor intensidad en el tiempo de lluvias. Un análisis más certero debe considerar la variación de la precipitación en el tiempo e incluso la evaporación.
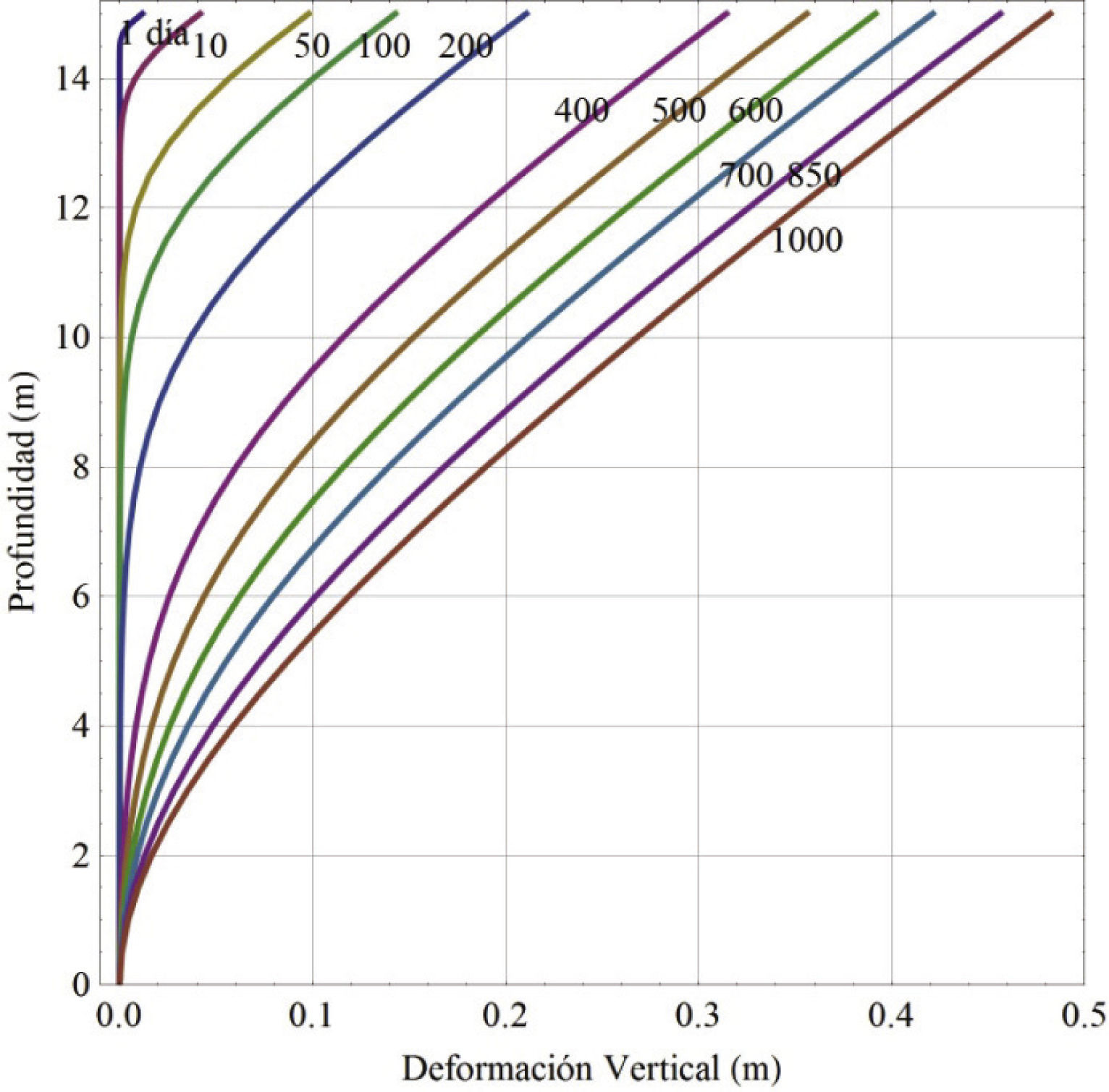
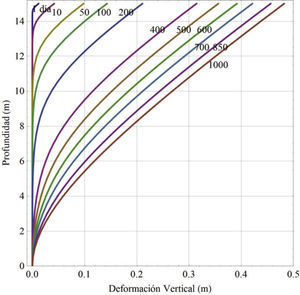
Cálculo de los asentamientos del suelo en el tiempoPara darse una idea concreta del significado de los cambios de contenido de humedad desde el punto de vista de asentamientos de colapso en el tiempo, se tomó como referencia una succión inicial de 220kPa y el tiempo se varió según lo que se mostró en la figura 8, para el cálculo se integró la ecuación (8), con los tiempos mencionados a distintas profundidades. En la figura 9 se muestra una gráfica de asentamiento de colapso respecto a la profundidad y al tiempo. El asentamiento es mayor en la parte superior (15 m), se va incrementando a medida que va infiltrándose el agua, se puede observar que después de 50 días de lluvia continua se tienen asentamientos superficiales de 10cm, que es el espesor típico de una carpeta de un pavimento; también se puede notar que la profundidad de influencia es de 3m. Para el presente análisis se estima un asentamiento máximo de 48cm en 2 años con 8 meses con 26 días (3.63%), esto para una infiltración continua.
La simulación de infiltración continua, de los 50 días de lluvia mencionados, no es una condición real sobre el terraplén. Desde el punto de vista práctico se deben revisar las condiciones de contorno de cada tramo carretero en particular, la infiltración depende de las obras de drenaje existentes, de los flujos de agua en secciones de corte, de los contenidos de agua en terreno de desplante hacia el terraplén y de la profundidad del nivel de aguas freáticas, por tanto, el tiempo se puede reducir o aumentar. Las variaciones de las condiciones de contorno de infiltración, dan como resultado deformaciones de colapso de distinta magnitud en distintas zonas del camino. Estas deformaciones de colapso diferenciales generan condiciones de operación desfavorables de los vehículos que producen accidentes. Es claro entonces que las deformaciones de colapso son significativas y pueden alterar el funcionamiento y mantenimiento de la Autopista. La velocidad de infiltración del agua es muy pequeña y provoca que los asentamientos se originen después de varios años, aumentando los gastos de mantenimiento y accidentes.
ConclusionesSe realizó un estudio para la estimación de las deformaciones de colapso en un terraplén representativo de la autopista Pátzuaro-Uruapan, con base en la teoría de suelos parcialmente saturados. Se muestreó el limo característico de esta región, con el que se construyeron buena parte de los terraplenes, se hicieron ensayos rutinarios y se obtuvo su curva de retención, además de estimar la función de permeabilidad respecto a la succión. Adicionalmente se realizaron ensayos de consolidación unidimensional en un suelo parcialmente-saturado, compactado con contenido de humedad constante, obteniendo los parámetros del Modelo Básico de Barcelona para la estimación del colapso por humedecimiento. En los ensayos de laboratorio se obtuvieron colapsos de 2.9% con el grado de compactación típico de 90% y de 1% con un grado de compactación mayor al establecido, 93%. De acuerdo con la Normativa Española el suelo no es colapsable, si el suelo se compactase a 93%, pero dadas las condiciones de compactación de la normativa Mexicana (90%) el suelo es colapsable. Por tanto, se concluye que la normativa Mexicana de compactación de terraplenes considera un grado de compactación bajo que favorece el colapso por humedecimiento para este tipo de suelo. Los datos de los ensayos se utilizaron para solucionar la ecuación de flujo transitorio para el caso de infiltración en una dimensión y calcular los asentamientos por infiltración.
El cálculo de los asentamientos por colapso se llevó a cabo de manera desacoplada de la infiltración con el modelo elasto-plástico BBM, con base en la variación de la succión que se obtuvo durante el periodo de la infiltración. Asimismo, se obtuvieron deformaciones de colapso para infiltración de 10cm para un periodo de 50 días, estos se podría presentar en la primera temporada de lluvias y si se toman las condiciones de contorno generales del camino se puede reducir el tiempo o aumentar; con ello se concluye que las deformaciones son significativas, pero que dependen fuertemente del tiempo de infiltración y las condiciones de contorno. Como no llueve todo el año, se concluyó que estas deformaciones se presentan en un tiempo mayor; para realizar una mejor estimación del tiempo es necesario considerar variaciones de lluvia, evaporación y la geometría del camino con todas las posibles infiltraciones. Se debe hacer notar que no existe normativa de diseño en México para limitar este tipo de asentamientos, al contrario, la actual norma de terraplenes lo favorece si se utiliza 90% de grado de compactación.
Los resultados enfatizan el problema de asentamientos de los terraplenes que se presentan en la autopista Pátzcuaro-Uruapan, que han causado incremento en los costos de operación de la autopista, así como accidentes. Las principales reparaciones que se realizan en los tramos de terraplén son re-nivelaciones con concreto asfáltico, lo que resulta costoso. Sin embargo, existen recomendaciones para elevar el grado de compactación a 95 y 95±2% para suelos de terraplén de calidad deseable y adecuada en autopistas, situación que disminuiría el problema.
Se pone de manifiesto la necesidad de utilizar las bases de la teoría de suelos parcialmente saturados para la predicción del comportamiento de los terraplenes, en este caso para carreteras, y realizar estudios adicionales a los que se realizan en la actualidad. Ya que un porcentaje importante se construye en zonas de suelos parcialmente saturados y con suelos parcialmente saturados. Es necesario realizar estudios de este tipo para sensibilizarnos con la problemática y aplicar en la práctica soluciones adecuadas, realizando un mejor diseño de los terraplenes.
Citación estilo Chicago
Citación estilo ISO 690
Carlos Chávez-Negrete. Estudió la licenciatura de ingeniería civil en la Universidad Michoacana de San Nicolás de Hidalgo (UMSNH), posteriormente la maestría en vías terrestres en la Universidad Autónoma de Chihuahua, posteriormente ingresó a la UMSNH como profesor investigador asociado. En el año 2004 terminó sus estudios de doctorado en ingeniería del terreno en la Universidad Politécnica de Cataluña, España. Actualmente es profesor investigador titular de la Facultad de Ingeniería Civil de la UMSNH y profesor de la maestría en infraestructura del transporte en la rama de la vías terrestres.
José de Jesús Espinosa-Arreola. Ingeniero civil por la Universidad Michoacana de San Nicolás de Hidalgo (UMSNH). Laboró en el Centro SCT Michoacán, en el área de Carreteras Alimentadoras. Es maestro en ingeniería en infraestructura del transporte en la rama de las vías terrestres por la UMSNH. Actualmente es ingeniero en diseño de mezclas asfálticas Nivel III y IV de protocolo AMAAC en SemMaterials México.
Jorge Alarcón-Ibarra. Estudió ingeniería civil en el instituto tecnológico y de estudios superiores de Occidente en Guadalajara, y el doctorado en ingeniería civil en la Universidad Politécnica de Cataluña, en Barcelona, España. Ha participado en varios proyectos de investigación y ha presentado ponencias y artículos especializados tanto en México como en el extranjero. Actualmente es profesor investigador titular “A” en la Universidad Michoacana de San Nicolás de Hidalgo y profesor de la maestría en infraestructura del transporte en la rama de la vías terrestres.
José Eleazar Arreygue-Rocha. Realizó la licenciatura en ingeniería civil en la Universidad Michoacana de San Nicolás de Hidalgo (UMSNH), cursó la especialidad en vías terrestres en la UMSNH y la maestría en materiales. Estudió el doctorado en ingeniería geológica en la Universidad de Florencia, Italia. En 1999 se incorporó como profesor investigador titular de la Facultad de Ingeniería Civil de la UMSNH y profesor de la maestría en infraestructura del transporte en la rama de la vías terrestres.