INTRODUCCIÓN A LOS MODELOS FARMACOECONÓMICOSDETERMINÍSTICOS Y ESTOCASTICOS
Un modelo puededefinirse como un esquema teórico, generalmente en formamatemática, de un sistema o de una realidad compleja que seelabora para facilitar su comprensión y el estudio de sucomportamiento (1). Es decir, los modelos sirven para hacersimulaciones de realidades complejas como los procesos sanitarios.Un caso particular de éstos son los modelosfarmacoeconómicos, que pueden ser de gran complejidad, yaque utilizan los resultados de eficacia obtenidos a partir de otrosmodelos, como los ensayos clínicos o losmeta-análisis de éstos, así como estimacionesrelativas a la práctica clínica, el consumo derecursos sanitarios y los costes relacionados (2).
Estos modelostienen como objetivo comparar la eficiencia, entendida como elcoste por unidad de efectividad de dos alternativasterapéuticas o preventivas, generalmente fármacos.Debido a la necesidad de hacer estimaciones, los modelos no tienenla misma validez que los ensayos clínicos de eficiencia,pero tienen la ventaja sobre éstos de ser menos costosos yde ejecución más rápida (3).
Deberíanutilizarse modelos preliminares en las fases tempranas deldesarrollo de nuevos fármacos como ayuda a lascompañías farmacéuticas en la decisiónde continuar o interrumpir el desarrollo. Posteriormente,disponiendo de los primeros datos de eficacia obtenidos de losensayos clínicos de fase III, deberían realizarsemodelos de simulación más maduros para serincorporados al expediente de registro del medicamento, siendoasimismo de utilidad para la discusión del precio y lanegociación del reembolso del nuevo fármaco con lasautoridades sanitarias (3).
En laevaluación económica de un proceso sanitario seconsideran dos posibles modelos: los determinísticosy los estocásticos. Los modelosdeterminísticos se definen como aquellos que computan lascantidades de interés (por ejemplo, el efecto deltratamiento, las probabilidades de supervivencia, el númerode personas que termina en diferentes estados de salud)directamente mediante fórmulas algebraicas, sin utilizartécnicas de simulación de eventos para modelizar elproceso (4). Es decir, en los modelos determinísticos seutiliza el número medio de eventos que se produce en lapoblación, ya que se asume que existe certidumbre en losdatos disponibles sobre los eventos sanitarios. Por ejemplo, si latasa anual de mortalidad específica de una enfermedad es del10%, se asume que exactamente el 10% de las personas de una cohortemorirán por esa enfermedad cada año (5). Sin embargo,los modelos estocásticos para los procesos sanitarios sonmodelos probabilísticos que, a diferencia de losdeterminísticos, utilizan la incertidumbre como parte delcálculo, por lo que se emplea la aleatorización parasimular las probabilidades de distribución de los eventosque podrían darse por efecto del azar. Por ejemplo, parasimular una probabilidad de morir del 3% en un determinadoaño se simularía la historia de cada individuo de lacohorte mediante el empleo de una tabla de númerosaleatorios que representase una probabilidad de ocurrencia de loseventos entre 1 y 100. Este proceso se repite para cada individuode la cohorte un elevado número de veces, normalmente milesde veces, por lo que una vez finaliza la simulación seobtiene un valor medio que teóricamente seaproximaría al valor medio utilizado en los cálculosdeterminísticos (5).
El modeloestocástico más frecuentemente utilizado es eldenominado modelo de Markov (6). Pero, ¿quién fueMarkov? Andrei Andreyevich Markov fue un matemático ruso quenació en Ryazan en 1856 y murió en Petrogrado (laactual San Petersburgo) en 1922. Fue profesor en la universidad deesta ciudad desde 1886 y es reconocido en la actualidadprincipalmente por su estudio sobre las denominadas cadenas deMarkov, que dio lugar posteriormente a la teoría de losprocesos estocásticos (7, 8). El objetivo del presentetrabajo es revisar brevemente la utilidad de los modelos de Markoven el análisis farmacoeconómico.
MODELOS DEMARKOV: CONCEPTOS BASICOS
En primer lugardebe quedar claro que ningún modelo es unarepresentación perfecta de la realidad. Su validez dependede lo razonables que sean las estimaciones o suposiciones tomadas yde su grado de aproximación a la realidad (5).
¿Qué es un modelo de Markov?
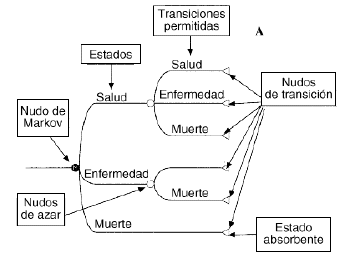
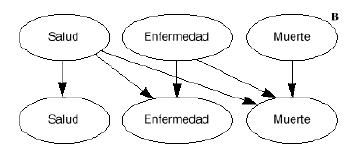
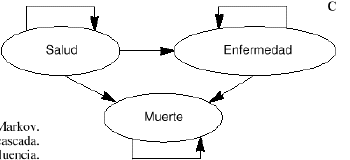
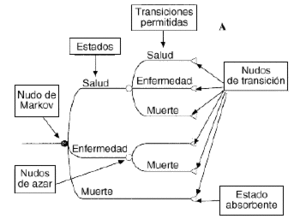
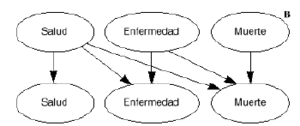
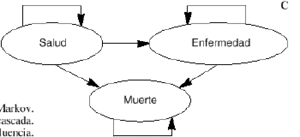
Un modelo deMarkov aplicado al campo sanitario puede definirse como un modeloestocástico de una enfermedad en el que se asume que elpaciente se encuentra siempre en uno de un número finito deestados de salud (denominados estados de Markov), los cualesdeben ser exhaustivos (es decir, todos los posibles) y mutuamenteexcluyentes (un individuo no puede estar en dos estados al mismotiempo). Los estados pueden ser de dos tipos: absorbentes (aquellosque no pueden abandonarse, siendo el más habitual y obvio elestado de «muerte») y no absorbentes (cualquier estadodesde el que se puede pasar a otro distinto). Los acontecimientosse modelizan como pasos o transiciones de unos estados aotros que se producen en períodos uniformes de tiempo (quese denominan ciclos de Markov) y con una probabilidad detransición que depende del estado en el que se encuentreel individuo en cada momento (9-11). Los modelos de Markov puedenrepresentarse gráficamente como una variante de losárboles de decisión empleados en los modelosdeterminísticos, como diagramas en cascada, o bien como undiagrama de influencias (8) (Figs. 1A, B y C, respectivamente).
Figura 1.--Posibles representaciones gráficas delos modelos de Markov. A: como árboles de decisión.B: como diagramas en cascada. C: como diagramas deinfluencia.
¿Cuándo debe utilizarse?, ¿conqué condiciones?
Puede estarjustificado utilizar un modelo de Markov cuando se trata de eventosrepetitivos, irreversibles y de larga duración (9). En casode realizarse, las condiciones generales de los modelos de Markovson las siguientes (8):
-- Sólose permiten unas determinadas transiciones entre estadospreviamente establecidas.
-- Laduración de los ciclos de Markov, que es arbitraria, debeser constante a lo largo de la simulación.
-- Cada pacientesólo puede hacer una transición en cadaciclo.
-- Todos lospacientes están sometidos a las mismas probabilidades detransición.
Ventajas einconvenientes de los modelos de Markov
Los modelos deMarkov ayudan a modelizar eventos sanitarios complejos que puedensimplificarse en exceso con los modelos determinísticos. Sonespecialmente útiles para modelizar enfermedadescrónicas (12). La modelización de Markov intentasimular de una manera más «realista» lo queocurre en el proceso de la enfermedad. Sin embargo, en algunasocasiones este tipo de modelo puede ser inviable debido a lainsuficiencia de los datos disponibles. Por ejemplo, en modelos muycomplejos puede ser difícil establecer la totalidad de lasprobabilidades de transición entre los estados de salud(8).
Por otra parte,en los modelos se hace una suposición bastante fuerte, ladenominada suposición markoviana. De acuerdo conésta el modelo carece de «memoria» y se asumeque conociendo únicamente el estado de salud presente de unpaciente es posible simular la evolución futura del mismo;es decir, se asume que todos los pacientes que se encuentran en unestado de salud, en un momento concreto, tienen el mismopronóstico, independientemente de su estado previo. Portanto, un paciente que pasa del estado «sano» al de«enfermo» tendría el mismo pronóstico queotro paciente «enfermo» que transcurrido el ciclosiguiese en el mismo estado de «enfermo». Estasuposición del modelo no se ajusta estrictamente a larealidad de numerosas enfermedades, por lo que supone uninconveniente de los modelos de Markov (9).
Tipos demodelos de Markov
Hay dos tipos demodelos de Markov: las denominadas cadenas de Markov, en lasque las probabilidades de transición permanecen constantes alo largo de toda la simulación, y aquellos en los que lasprobabilidades de transición varían con el tiempo,denominados procesos de Markov. Las cadenas de Markov sonaplicables a problemas sanitarios con un horizonte temporal corto,en los que existe la posibilidad de que las probabilidades detransición permanezcan constantes en dicho período.Sin embargo, en las enfermedades crónicas de largaduración generalmente se produce con la edad un aumento delas tasas de morbilidad y mortalidad. Por ello en estos casos espreferible aplicar procesos de Markov. El problema es que ennumerosas ocasiones no se dispone de tasas de morbilidad omortalidad, por intervalos de edad, que sean fiables, motivo por elcual es difícil que a su vez lo sean las correspondientesprobabilidades de transición (8, 9).
Pasos en larealización de un modelo de Markov
Los pasos quedeben darse para la elaboración de un modelo de Markov sonlos siguientes (8, 9):
-- Definir losestados de salud.
-- Establecerlas transiciones permitidas entre los estados.
-- Definir laamplitud de los ciclos (meses, años, etc.).
-- Fijar lasprobabilidades de transición entre los estados.
-- Determinar lautilidad y los costes de cada uno de los estados.
-- Resolver lasimulación determinada por el modelo.
Laresolución del modelo puede hacerse mediante tresmétodos (9, 12): la simulación de una cohortehipotética; la simulación de Monte Carlo, en la quese simula el seguimiento individual de un elevado número depacientes (por ejemplo, 10.000), y, finalmente, las matricesfundamentales, que sólo pueden utilizarse para cadenas deMarkov, ya que precisan probabilidades de transiciónconstantes.
En los dosejemplos siguientes se revisan los aspectos básicos de lasimulación de una cohorte de pacientes para cadenas yprocesos de Markov, respectivamente.
CADENAS DEMARKOV: EJEMPLO TEORICO
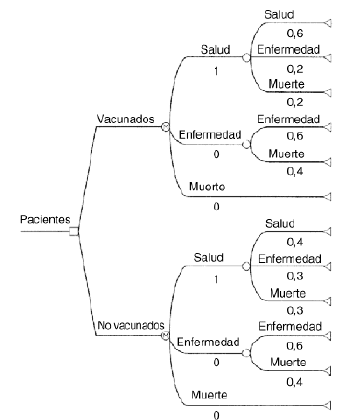
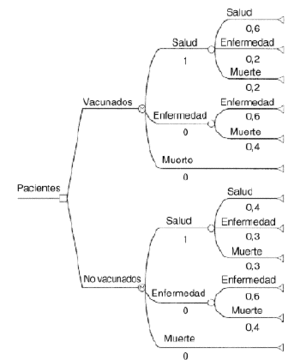
Se plantea unejemplo teórico muy simple de cadena de Markov. Se comparala eficiencia de dos estrategias o alternativas: administrar o nouna vacuna, que previene la aparición de una enfermedad quepuede ser mortal. Hay tres estados posibles: salud, enfermedad ymuerte. Todos los individuos de una cohorte hipotéticacomenzarían la cadena en el estado «salud». Lastransiciones permitidas a partir del estado inicial seríantres: seguir con salud, enfermar o morir; un paciente enfermopodría a su vez seguir enfermo o morir, y finalmente, lamuerte sería el estado absorbente. Todos los individuosterminarían muriendo si transcurriese el tiempo suficiente(8) (Fig. 2).
Figura 2.--Ejemplo teórico de cadena de Markov(vacunación).
La amplitud delciclo de Markov debe ajustarse a la evolución y a loscambios naturales de la enfermedad de que se trate. En el ejemploconsideramos que los pacientes tienen probabilidades de transitarentre los estados una vez cada año.
El númerode ciclos de la simulación también debe fijarse deacuerdo con la evolución natural de la enfermedad y laexpectativa de vida de los pacientes afectados. En nuestro ejemploqueremos saber qué ocurriría después de cincociclos de Markov, es decir, cinco años después de lavacunación o de no vacunar (8).
Las transicionesse producirían de acuerdo con probabilidades constantes entodos los ciclos. Éstas se indican en la tabla 1, tanto para pacientes vacunados como parapacientes no vacunados. Asimismo se representan en el árbolde Markov, según la figura 2. Los pacientes vacunadostendrían una mayor probabilidad de permanecer sanos, portanto una menor probabilidad de enfermar y de morir que lospacientes no vacunados.
| Tabla 1. Probabilidades de transición delejemplo de cadena de Markov | |||
| Hasta | |||
| Salud | Enfermedad | Muerte | |
| Con vacunación | |||
| --Desde: | |||
| -- * Salud | 0,6 | 0,2 | 0,2 |
| -- * Enfermedad | 0 | 0,6 | 0,4 |
| -- * Muerte | 0 | 0 | 1 |
| Sin vacunación | |||
| --Desde: | |||
| -- * Salud | 0,4 | 0,3 | 0,3 |
| -- * Enfermedad | 0 | 0,6 | 0,4 |
| -- *Muerte | 0 | 0 | 1 |
Lasprobabilidades anuales de transición de Markov debencalcularse con la fórmula:
pt = 1 ert
siendopt la probabilidad de transición yrt la tasa de ocurrencia anual del evento, en tanto porciento.
De acuerdo conlas probabilidades de transición así establecidas, laevolución de una cohorte de individuos, vacunados o novacunados, se indica en la tabla 2. Alcabo de cinco años en la cohorte de 1.000 individuosvacunados habría 68 pacientes sanos más y sehabrían evitado 95 muertes en comparación con lacohorte de no vacunados.
| Tabla 2. Simulaciónde una cohorte para el modelo ilustrativo de una cadena deMarkov | |||||
| Ciclo(año) | Estado desalud | Total | |||
| Salud | Enfermedad | Muerte | |||
| Vacunados | 0 | 1.000 | 0 | 0 | 1.000 |
| 1 | 600 | 200 | 200 | 1.000 | |
| 2 | 360 | 240 | 400 | 1.000 | |
| 3 | 216 | 216 | 568 | 1.000 | |
| 4 | 130 | 173 | 698 | 1.000 | |
| 5 | 78 | 130 | 793 | 1.000 | |
| No vacunados | 0 | 1.000 | 0 | 0 | 1.000 |
| 1 | 400 | 300 | 300 | 1.000 | |
| 2 | 160 | 300 | 540 | 1.000 | |
| 3 | 64 | 228 | 708 | 1.000 | |
| 4 | 26 | 156 | 818 | 1.000 | |
| 5 | 10 | 101 | 888 | 1.000 | |
Para ilustrar elejemplo se supone que los estados de salud tendrían loscostes (en unidades monetarias, UM) y las utilidades (comoaños de vida ajustados por calidad, AVAC)siguientes:
-- Salud: 1.000UM y 1 AVAC.
-- Enfermedad:100.000 UM y 0,7 AVAC.
-- Muerte: 500UM y 0 AVAC.
De acuerdo conestos valores, los costes incrementales, las utilidadesincrementales y el análisis coste-utilidad (que seobtendrían del «plegado» del árbol dedecisiones, consistente en multiplicar los costes y/o lasutilidades de cada rama del árbol por las correspondientesprobabilidades de transición) se expresan en la tabla 3. En este ejemplo no sería necesarioefectuar el análisis coste-utilidad incremental (costeincremental/utilidad incremental), ya que la alternativa de vacunarsería más efectiva (con una diferencia a su favor de0,834 AVAC) e igualmente costosa que la de no vacunar, por lo que,expresado en la terminología farmacoeconómica, laprimera alternativa dominaría a la segunda (tabla3).
| Tabla 3. Resultados delejemplo de análisis farmacoeconómico, ilustrativo deuna cadena de Markov | |||
| Estrategia | Costes (UM) | Utilidades(AVAC) | Coste/utilidades(UM/AVAC) |
| Vacunación | 624.625 | 2,374 | 263.156 |
| No vacunación | 624.208 | 1,540 | 405.216 |
| Diferencia | 417 | 0,834 | 142.060 |
| A.coste-utilidad incremental | La estrategia de vacunadomina a la estrategia de no vacunar | ||
PROCESOS DEMARKOV: EJEMPLO SOBRE LA TERAPIA HORMONALSUSTITUTIVA
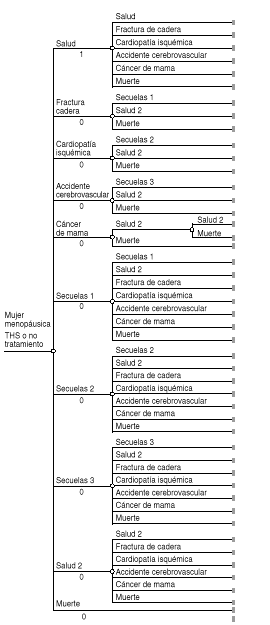
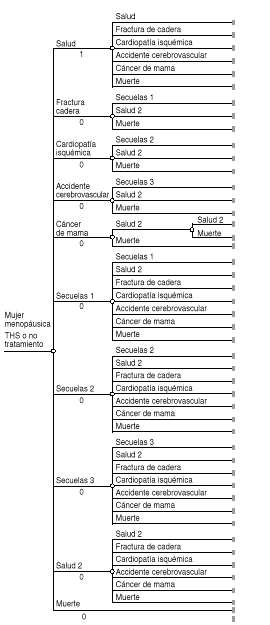
Como se dijoanteriormente, los procesos de Markov son aquellos en los que lasprobabilidades de transición varían con el tiempo.Como ejemplo de esta metodología se plantea un modelofarmacoeconómico de la terapia hormonal sustitutiva (THS)con estrógenos más progestágenos de lasmujeres postmenopáusicas no histerectomizadas,comparándola con la actitud de no tratarlas. Debido alcarácter estocástico de las complicacionespatológicas de la menopausia --son estados de salud como lasfracturas de cadera (FC), la cardiopatía isquémica(CI), los accidentes cerebrovasculares (ACV) o el cáncer demama (CM) que se producen aleatoriamente durante períodosprolongados de tiempo--, la historia natural de las mujeresmenopáusicas se presta a la modelización mediante unproceso de Markov. Además de las complicaciones indicadas,también deberían considerarse los siguientes estados:secuelas de la FC (secuelas 1), secuelas de la CI (secuelas 2),secuelas del ACV (secuelas 3), volver a tener buena salud una vezsuperada una complicación o una secuela (salud 2) y, porsupuesto, el estado de «salud» inicial (definido comola ausencia de complicaciones patológicas) y lamuerte.
El paso otransición de un estado a otro ocurriría al final deperíodos discretos de tiempo (ciclos de Markov), que debidoa la historia de la enfermedad podrían ser de un añode duración. Las transiciones permitidas entre los estadosse representan en la figura3.
Figura 3.--Ejemplo teórico de proceso de Markov(terapia hormonal sustitutiva).
Seasumiría que toda la cohorte de mujeres está sanainicialmente, es decir, a los cincuenta años de edad, y quea partir de entonces las mujeres empiezan a transitar a los otrosestados, de acuerdo con unas probabilidades de transición.Éstas se establecerían, por intervalos de edad, apartir de los riesgos relativos de padecer complicaciones (9).Debido a la carencia de estudios epidemiológicos realizadosen la población española podría asumirse quelos riesgos de las complicaciones de la menopausia en Españaserían similares a los estimados en otros países denuestro entorno (13, 14), considerando que la duración deltratamiento (horizonte temporal) es de quince años y que losbeneficios u otros efectos de la THS se prolongan durante unperíodo adicional igual al del tratamiento (13, 15, 16)(tabla 4). En la tabla 5 se recogen las probabilidades detransición desde el estado de salud con o sinTHS.
| Tabla 4. Suposicionesestándares acerca del riesgo de padecer compliacionesdespués del tratamiento durante quinceañosde mujeres de cincuenta años de edad conútero, con terapia hormonal sustitutiva (THS), conestrógenos más progestágenosexpresados comoriesgos relativos (RR) | ||||||||||
| Edad en años de lasmujeres de la cohorte | ||||||||||
| 50-54 | 55-59 | 60-64 | 65-69 | 70-74 | 75-79 | 80-84 | 85-89 | 90-94 | 95-99 | |
| Fractura de cadera | 0,80 | 0,40 | 0,40 | 0,40 | 0,40 | 0,80 | 1,00 | 1,00 | 1,00 | 1,00 |
| Cardiopatíaisquémica | 1,00 | 0,88 | 0,75 | 0,8 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| Enfermedadcerebrovascular | 1,00 | 0,94 | 0,88 | 0,88 | 0,94 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| Cáncer de mama | 1,00 | 1,00 | 1,30 | 1,30 | 1,30 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| Tabla 5. Probabilidades de transición (de estar encada estado de salud) un año después de comenzar enel estado «salud» | |||||||
| Estado de salud unaño después de comenzar en el estado«salud» | |||||||
| Edad | Salud | FC* | CI* | ACV* | CM* | Muerte | |
| Sin THS | |||||||
| 50-54 | 0,99485 | 0,00008 | 0,00091 | 0,00059 | 0,00235 | 0,00122 | |
| 55-59 | 0,99043 | 0,00021 | 0,00286 | 0,00181 | 0,00275 | 0,00194 | |
| 60-64 | 0,98900 | 0,00046 | 0,00286 | 0,00181 | 0,00275 | 0,00312 | |
| 65-69 | 0,98109 | 0,00111 | 0,00546 | 0,00445 | 0,00259 | 0,00530 | |
| 70-74 | 0,97441 | 0,00298 | 0,00546 | 0,00445 | 0,00259 | 0,01011 | |
| 75-79 | 0,94004 | 0,00548 | 0,00915 | 0,01464 | 0,00183 | 0,02886 | |
| 80-84 | 0,91816 | 0,01491 | 0,00915 | 0,01464 | 0,00183 | 0,04131 | |
| 85-89 | 0,88288 | 0,02077 | 0,00915 | 0,01464 | 0,00183 | 0,07073 | |
| 90-94 | 0,87869 | 0,02496 | 0,00915 | 0,01464 | 0,00183 | 0,07073 | |
| 95-99 | 0,87713 | 0,02652 | 0,00915 | 0,01464 | 0,00183 | 0,07073 | |
| Con THS | |||||||
| 50-54 | 0,99482 | 0,00006 | 0,00091 | 0,00059 | 0,00235 | 0,00127 | |
| 55-59 | 0,99092 | 0,00008 | 0,00252 | 0,00170 | 0,00275 | 0,00203 | |
| 60-64 | 0,98931 | 0,00018 | 0,00215 | 0,00159 | 0,00358 | 0,00319 | |
| 65-69 | 0,98327 | 0,00044 | 0,00410 | 0,00392 | 0,00337 | 0,00490 | |
| 70-74 | 0,97683 | 0,00119 | 0,00480 | 0,00418 | 0,00337 | 0,00963 | |
| 75-79 | 0,94946 | 0,00438 | 0,00733 | 0,01173 | 0,00183 | 0,02527 | |
| 80-84 | 0,92708 | 0,01491 | 0,00733 | 0,01173 | 0,00183 | 0,03712 | |
| 85-89 | 0,89204 | 0,02077 | 0,00733 | 0,01173 | 0,00183 | 0,06630 | |
| 90-94 | 0,88811 | 0,02496 | 0,00733 | 0,01173 | 0,00183 | 0,06604 | |
| 95-99 | 0,88665 | 0,02652 | 0,00733 | 0,01173 | 0,00183 | 0,06604 | |
FC:fractura de cadera. CI: cardiopatía isquémica. ACV:accidente cerebrovascular. CM: cáncer de mama. | |||||||
A cada estado desalud debería asignársele un coste y una utilidadanuales (es decir, por ciclo) obtenidos, respectivamente, a partirde los correspondientes costes de los grupos relacionados por eldiagnóstico (GRD) y de las apreciaciones de los pacientes ode un panel de expertos en la menopausia.
Considerando unacohorte hipotética de mujeres postmenopáusicas, apartir de los cincuenta años de edad, las probabilidades detransición desde el estado de «salud», estimadaspara intervalos de edad de cinco años, se recogen en latabla 4.
La forma deresolución de los procesos de Markov es similar a la de lascadenas de Markov. Sin embargo, las probabilidades detransición variables complican considerablemente loscálculos, por lo que es conveniente efectuarlos mediante elmanejo de programas estadísticos.