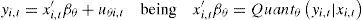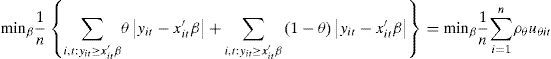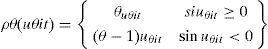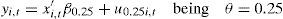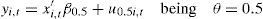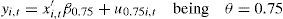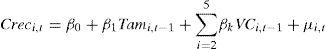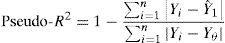In recent years, Brazil has been one of the countries with the biggest changes in the banking sector. The process of deregulation that began in 2002 has entailed the increase of the presence of foreign banking and the increase of competition, among other aspects. In this context, the objective of this study consists in contrasting Gibrat's Law in the Brazilian commercial banking during the period of 2002–2013 with the objective of contributing with evidence for the construction of a growth model for banking that will guide the financial policy of the country. For this, the quartile regression methodology is utilized, since we consider that it analyzes the relation between growth and the size of the entities more thoroughly than the empirical contrasts given by previous empirical evidence. The results obtained indicate that there is a non-linear relation in an inverted U form between growth and size in the Brazilian commercial banking. These results allow us to affirm that the relative dispersion of the sizes of the financial entities will tend to decrease in time and with this, the concentration of the sector.
En los últimos años Brasil ha sido uno de los países con mayores cambios en el sector bancario. El proceso de desregulación iniciado en 2002 ha conllevado el aumento de la presencia de banca extranjera y el incremento de la competencia, entre otros aspectos. En este contexto, el objetivo del presente estudio consiste en contrastar la Ley de Gibrat en la banca comercial brasileña durante el periodo 2002-2013 con el objeto de aportar evidencia para la construcción de un modelo de crecimiento para la banca que oriente la política financiera del país. Para ello se emplea la metodología de regresiones cuartílica que consideramos analiza de manera más exhaustiva la relación entre el crecimiento y el tamaño de las entidades que los contrastes empíricos aportados por la evidencia empírica previa. Los resultados obtenidos nos indican que existe una relación no lineal en forma de U invertida entre crecimiento y tamaño en la banca comercial brasileña. Estos resultados nos permiten afirmar que la relativa dispersión de los tamaños de las entidades financieras tenderá a reducirse en el tiempo y con ello la concentración del sector.
During recent decades, the financial sector has experienced significant changes due to the liberalization and deregulation of the markets, the technological changes, and the international financial crisis, which have entailed an increase in the degree of banking concentration and the size of the entities (Fernholz & Hoch, 2016).
Traditionally, the empirical studies on banking concentration have been based on the contrast of Gibrat's Law, which implies the absence of relation between size and growth, so that all entities have the same probability of growing (Alhadeff & Alhadeff, 1964; Benito, 2008; Fernholz & Hoch, 2016; Goodard, McKillop, & Wilson, 2002; Goddard, Molyneux, & Wilson, 2004; Goddard, McKillop, & Wilson, 2014; Rhoades & Yeats, 1974; Shehzad, De Haan, & Sholtens, 2013; Tschoegl, 1983; Vennet, 2001; Ward & McKillop, 2005; Wilson & Williams, 2000; Yeats, Irons, & Rhoades, 1975). However, these studies present two important limitations: they focus on the analysis of the banking sectors of developed countries, and the results obtained are mixed. For this reason, it would be advisable to expand the previous empirical evidence with the objective of obtaining conclusive results.
In this sense, it is important to indicate that in recent years it has been observed that the number of total assets of the entities has decreased in the Euro zone and the United Kingdom (BOE, 2010), while it has increased in other countries such as Brazil (Cull & Martínez Pería, 2013). Proof of this is the outstanding presence of foreign financial entities such as the Spanish Banco Santander and the British HSBC in the Brazilian banking sector, occupying the fifth and sixth position in market shares, respectively.
In this context, the objective of this study is to analyze the growth of banking in Brazil during the 2002–2013 period through the contrast of Gibrat's law and the incorporation of a series of methodological novelties regarding the traditional studies. Firstly, we analyze the growth-size relation by quartiles, as we consider that the attainment of mixed results by the previous empirical evidence can depend on the distribution of the growth rates of the entities, even finding different relations per entity groups. Secondly, we carried out an analysis to detect if the results found per quartiles significantly differ between them. In this manner, the quartile analysis allows us to carefully analyze the type of existing relation between the growth and size of the entities, finding that sometimes the relation between said variables is more complex than what could be assumed at first when carrying out an analysis on the total sample. Lastly, we applied a non-linear contrast of Gibrat's law with the objective of presenting conclusive results.
The main results obtained show that there is a significant relation between the growth and size of the entities, but this varies from positive to negative between the first and the third quartile. The difference of the results found between the first and the third quartile are significant, which confirms the non-linear relation in the shape of an inverted U between said variables. These results, therefore, make it possible for us to affirm that the relative dispersion of the sizes of the financial entities of Brazil will tend to decrease in time. This implies a decrease in sectorial concentration if the number of entities remains constant.
The rest of the work is structured as described below. In the second section, we present a review of the previous literature on the growth of banking. In the third section, we describe the characteristics of the sample. In the fourth section, the methodology used is presented. In the fifth section, we describe the empirical results obtained. Lastly, the sixth section presents the conclusions obtained from the work set.
Review of the literatureThe empirical study of banking growth has been traditionally linked to its relation with size through Gibrat's law (1931), which considers that corporate growth is a stochastic process that tends to the concentration of markets. Following Gibrat's law, we considered that the distribution of size resembles a long-normal distribution, because each company is the object of a series of shocks that are purely random and which in time tend to produce an asymmetrical distribution of this kind.
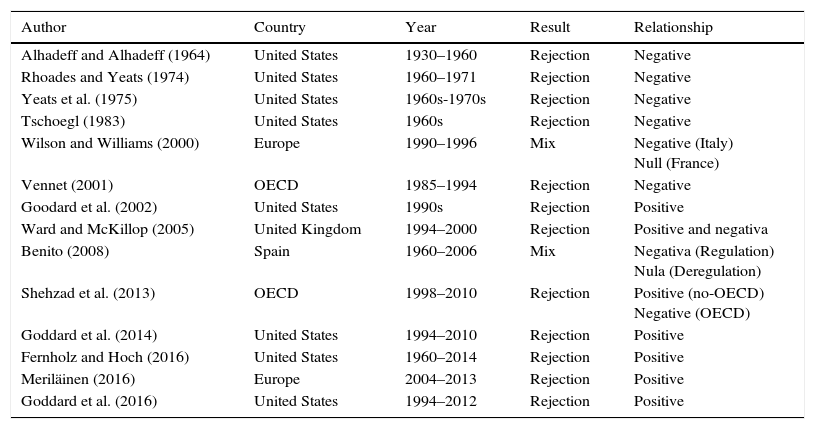
Table 1 presents a revision of works that analyze bank growth through the contrast of Gibrat's law. As we can see, these studies focus in the analysis of banking in the United States and Europe, presenting non-conclusive results. It is possible to observe a negative relation between banking growth and size in the first studies, implying that the smaller entities are the ones with the most growth (Alhadeff & Alhadeff, 1964; Rhoades & Yeats, 1974; Tschoegl, 1983; Vennet, 2001; Wilson & Williams, 2000; Yeats et al., 1975). Conversely, most recent works find evidence of a positive influence of size on growth, with the biggest entities being the ones with the most growth (Fernholz & Hoch, 2016; Goodard et al., 2002; Goddard et al., 2014; Goddard, McKillop, & Wilson, 2016; Meriläinen, 2016; Shehzad et al., 2013).
Gibrat's law in banking. Relation between size and growth.
| Author | Country | Year | Result | Relationship |
|---|---|---|---|---|
| Alhadeff and Alhadeff (1964) | United States | 1930–1960 | Rejection | Negative |
| Rhoades and Yeats (1974) | United States | 1960–1971 | Rejection | Negative |
| Yeats et al. (1975) | United States | 1960s-1970s | Rejection | Negative |
| Tschoegl (1983) | United States | 1960s | Rejection | Negative |
| Wilson and Williams (2000) | Europe | 1990–1996 | Mix | Negative (Italy) Null (France) |
| Vennet (2001) | OECD | 1985–1994 | Rejection | Negative |
| Goodard et al. (2002) | United States | 1990s | Rejection | Positive |
| Ward and McKillop (2005) | United Kingdom | 1994–2000 | Rejection | Positive and negativa |
| Benito (2008) | Spain | 1960–2006 | Mix | Negativa (Regulation) Nula (Deregulation) |
| Shehzad et al. (2013) | OECD | 1998–2010 | Rejection | Positive (no-OECD) Negative (OECD) |
| Goddard et al. (2014) | United States | 1994–2010 | Rejection | Positive |
| Fernholz and Hoch (2016) | United States | 1960–2014 | Rejection | Positive |
| Meriläinen (2016) | Europe | 2004–2013 | Rejection | Positive |
| Goddard et al. (2016) | United States | 1994–2012 | Rejection | Positive |
However, it is also important to point out that among all these studies, only two of them, those by Wilson and Williams (2000) and Benito (2008), have found evidence of acceptance for Gibrat's law, justifying this result by the influence of the regulation level to which the markets are subjected. Concretely, Wilson and Williams (2000) observe that the French financial entities have the same probability of growing, regardless of their size, and thus argue that said results are due to the French banking system is characterized by being too regulated in the years of study. On the other hand, Benito (2008) contrasts Gibrat's law for Spanish banks in the 1960–2006 period, itemizing the sample by regulation and deregulation periods. Said authors find that in periods of regulation, the small entities grow more quickly, while in deregulation stages no significant differences can be found; therefore, all entities grow in the same proportion, accepting Gibrat's law.
On the other hand, the integration and restructuration processes can affect the contrast of Gibrat's law in the banking sector. For this reason, it is important to take into consideration the works by Goddard et al. (2014, 2016). Concretely, Goddard et al. (2014) analyze the impact of the outputs and the internal growth generated by the processes of acquisitions and mergers on the distribution of the size of the credit entities in the United States during the 1994–2010 period. Conversely, Goddard et al. (2016) analyze the influence of the regulatory changes on matters of capital demand which occurred in the year 2000 in the United States for a set of 12,046 financial entities during the 1994–2012 period. The results obtained indicate that the larger and newer entities have greater probabilities of surviving and growing, rejecting Gibrat's law, and also finding that the smaller entities have a greater risk of disappearing through acquisitions or bankruptcy.
In this context, we considered it interesting to contrast Gibrat's law in the banking sector of an emerging country such as Brazil, since there has been a change in the structure of the Brazilian banking sector in recent years due to the various structural reforms that have allowed the liberalization of the markets and the entry of foreign entities. On the other hand, the results obtained will contribute with new empirical evidence for the banking sector due to the quartile analysis methodology utilized.
DatabaseThe banking sector in Brazil is characterized for having carried out a transformation and liberalization process that has made it possible for foreign banking to be present for the past 15 years (Chortareas, Gaza-García, & Girardonde, 2011). Nevertheless, the internationalization process of the financial entities has favored competition, which has an effect on the growth rates of the participating entities.
Cheng and Liao (2011) highlight that globalization has allowed foreign banks—especially those immersed in more developed financial systems—to expand toward emerging economies where occasionally they have become predominant due to the transfer of a big part of their business as consequence of the international financial crisis (Coleman & Feler, 2015). In the case of Brazil, it is important to point out that among the ten largest commercial banks by volume of total assets, the Spanish Banco Santander ranks third place, the British bank HSBC ranks fourth place, and places eight to ten are taken by the American bank Citibank, the Swiss bank Credit Suisse and the American bank JP Morgan Chase. Therefore, one of the reasons for this research lies in the importance of the banking sector of Brazil for the main commercial banks globally.
The analyzed period of time is comprised between the years 2002 and 2013, given that since 2002 Assunção (2013) finds evidence of a barrier removal for the entry of companies for the provision of financial services in Brazil. In this sense, it is important to indicate that during these years of study, the number of entities has varied due to the entry processes of foreign entities, as well as the mergers and takeovers that have taken place between national entities.
On the other hand, following the work by Goddard et al. (2004), the main variables for analysis are gathered in Table 2. Concretely, the growth is measured as the difference of corporate size logarithms between two consecutive periods, calculating corporate size through the logarithm of the assets figure of each company. Size occupies first place among the explicative variables for growth. According to Goddard et al. (2004), it is more difficult to produce a greater concentration when speaking about a sector with large companies. Secondly, we considered the profitability of financial entities, measured through the profitability of their own resources.
Description of the variables of the Brazilian banking sector.
| Variable | Definition | Acronym |
|---|---|---|
| Growth | Difference of logarithms of the size of two consecutive periods | Crec |
| Size | Natural logarithm of the asset figure | Tam |
| Cost effectiveness | Profitability of own resources | Rent |
| Capital ratio | Relationship between the capital of the entity and the assets of the entity | Cap |
| NPL ratio | Relationship between unpaid assets and total assets | Mor |
| Liquidity ratio | Ratio of net assets to total assets | Liq |
| Off balance sheet | Off-balance sheet assets on the entity's total assets | Obs |
Additionally, it is important to take into consideration that banking has responded to the concentration and pressure of competition by extending its service and financial products offer, increasing its Off-Balance Sheet (OBS)1 percentage, and improving the diversification of its portfolio and risk. Goddard et al. (2004) find mixed results for different European countries, indicating that there is indeed a positive relation between OBS and profitability, a negative relation for those banks that have increased the level of their OBS portfolio, and difficulties in maintaining their rates of return.
On the other hand, among the main indicators that explain the behavior of banking, we can find the capital and liquidity ratios. An excess of capital and liquidity represents a very conservative operation, which could be motive for idle resources, not taking advantage of investment opportunities, therefore, affecting profitability. In this sense, the default ratio that affects profitability is incorporated.
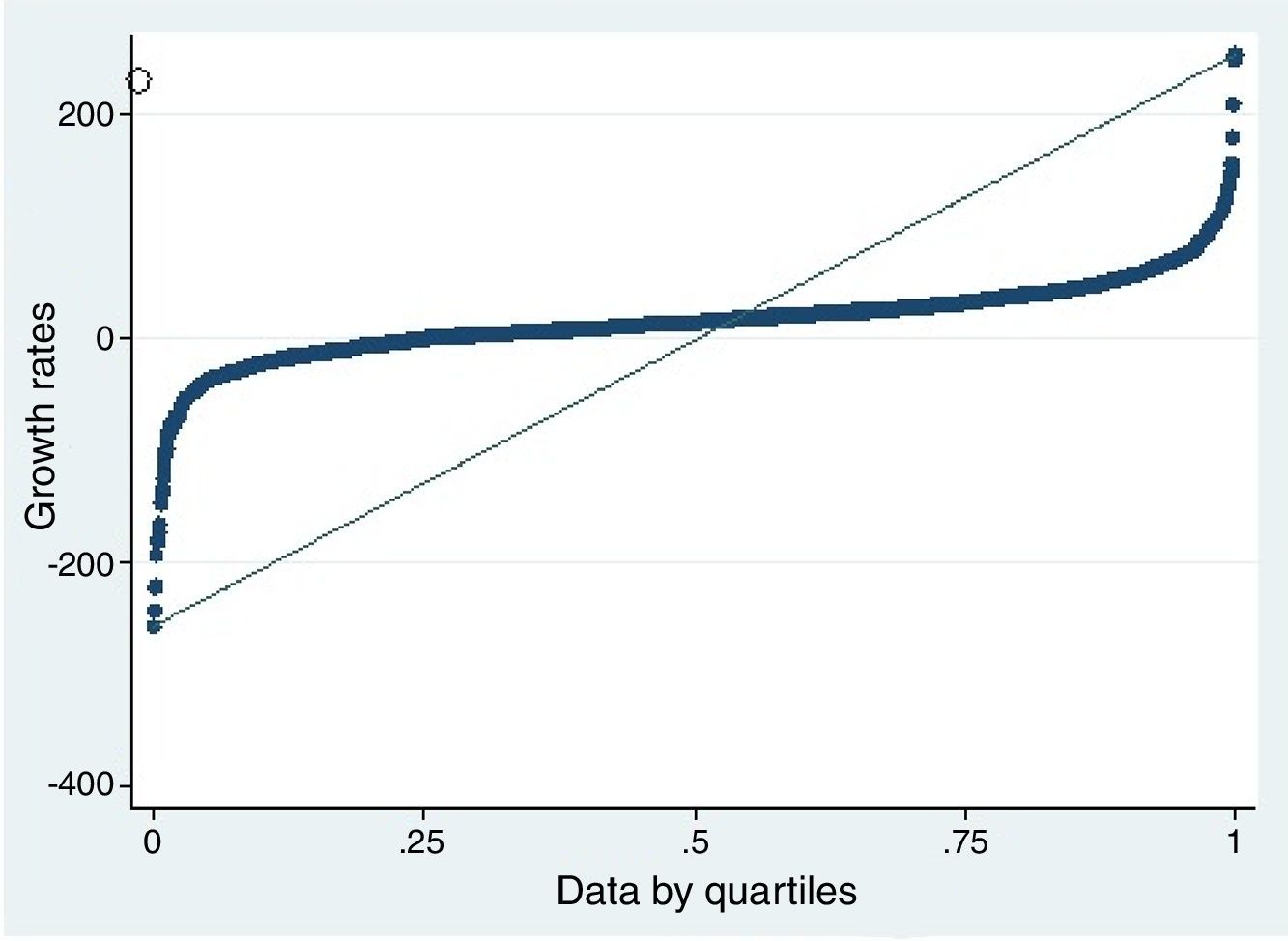
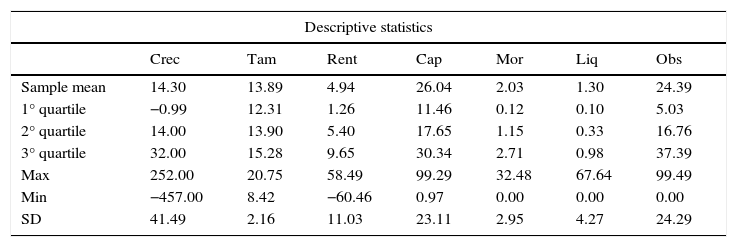
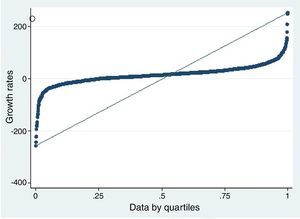
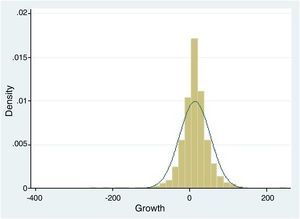
The descriptive statistics of the variable that are the subject of this study are presented in Table 3, both for the total sample and by quartiles. Regarding the descriptive statistics of the total sample, it is important to indicate that the entities in Brazil have had a median growth of 14.30%, situating the value of the first quartile in negative rates of 0.99%, the median in 14% and the third quartile in 32%. As can be observed in Fig. 1, which represents the distribution of the growth rates by quartile of the financial entities in Brazil, the growth rates increase per quartile but not uniformly, as the growth rates are distributed according to a standard, as shown below.
Descriptive statistics and correlation matrix.
| Descriptive statistics | |||||||
|---|---|---|---|---|---|---|---|
| Crec | Tam | Rent | Cap | Mor | Liq | Obs | |
| Sample mean | 14.30 | 13.89 | 4.94 | 26.04 | 2.03 | 1.30 | 24.39 |
| 1° quartile | −0.99 | 12.31 | 1.26 | 11.46 | 0.12 | 0.10 | 5.03 |
| 2° quartile | 14.00 | 13.90 | 5.40 | 17.65 | 1.15 | 0.33 | 16.76 |
| 3° quartile | 32.00 | 15.28 | 9.65 | 30.34 | 2.71 | 0.98 | 37.39 |
| Max | 252.00 | 20.75 | 58.49 | 99.29 | 32.48 | 67.64 | 99.49 |
| Min | −457.00 | 8.42 | −60.46 | 0.97 | 0.00 | 0.00 | 0.00 |
| SD | 41.49 | 2.16 | 11.03 | 23.11 | 2.95 | 4.27 | 24.29 |
| Matrix of correlations | |||||||
|---|---|---|---|---|---|---|---|
| Crec | Tam | Rent | Cap | Mor | Liq | Obs | |
| Crec | 1.00 | ||||||
| Tam | 0.14 | 1.00 | |||||
| Rent | 0.25 | 0.16 | 1.00 | ||||
| Cap | −0.17 | −0.64 | −0.12 | 1.00 | |||
| Mor | −0.15 | −0.03 | −0.19 | −0.10 | 1.00 | ||
| Liq | −0.00 | −0.07 | 0.04 | 0.02 | −0.06 | 1.00 | |
| Obs | −0.02 | −0.01 | −0.00 | 0.25 | −0.31 | −0.08 | 1.00 |
On the other hand, banking in Brazil presents an average profitability of 4.94% and an average capital ratio level of 26.04%. The average diversification of the OBS product portfolio is of 24.39%. Furthermore, the levels of liquidity and the average default rate are low but positive, with 1.30% and 2.03%, respectively. Lastly, the correlation matrix shows us how growth is positively correlated with size and profitability, and is negatively correlated with the rest of the explicative variables.
MethodologyAs has been commented in the review of the literature, one of the aspects that stands out in the study of growth has been the evolution of the methodology. Thus, the previously analyzed studies have utilized different techniques, such as ordinary least squares (OLS), fixed effects (FE), and the generalized method of moments (GMM) based on the development of the panel data methodology. This makes it possible to model the unobservable methodology that exists between the different companies through the decomposition of the error term into three components, allowing to increase the number of observations as well as the degrees of freedom of the models and, consequently, the consistency of the results.
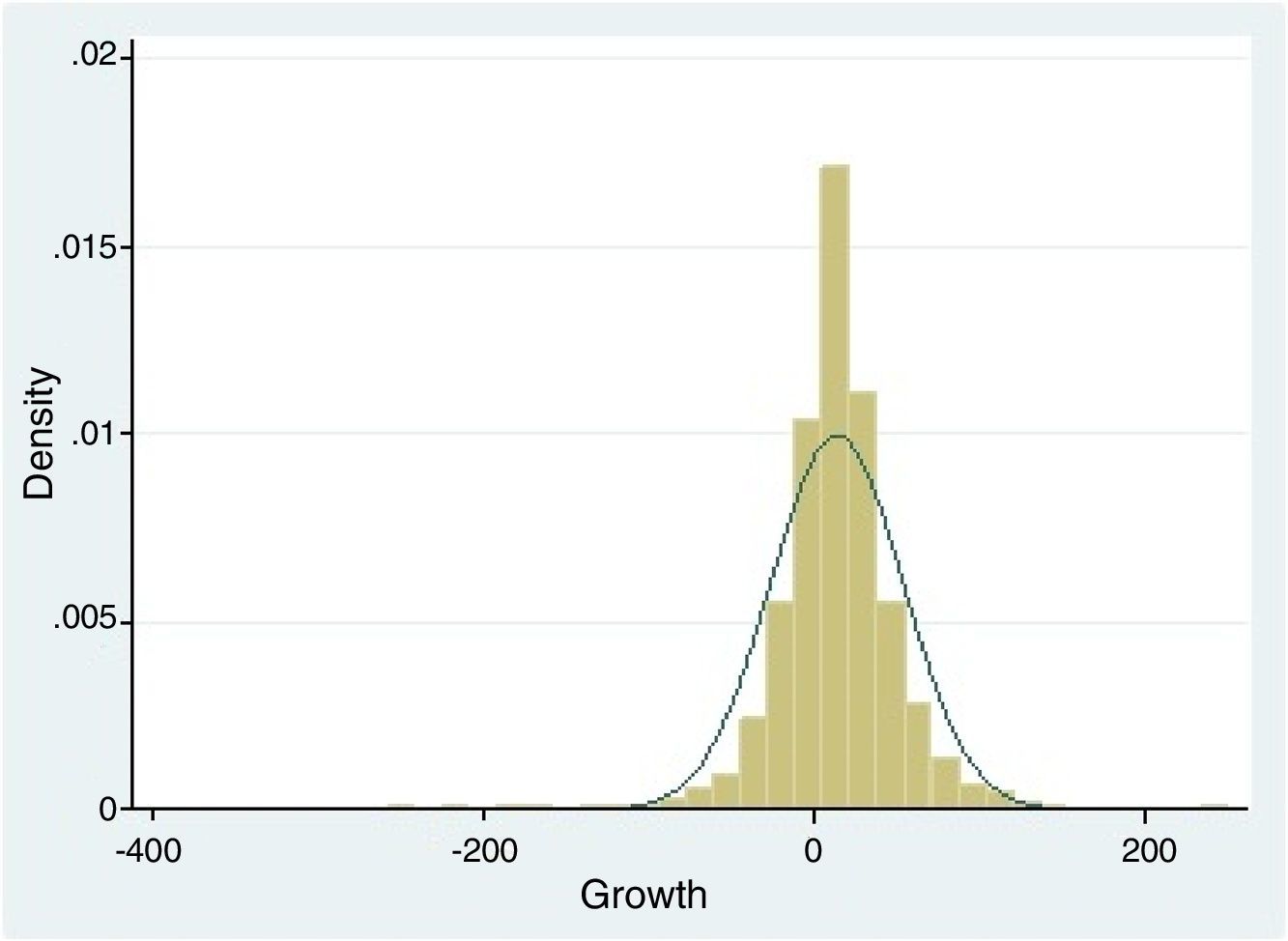
However, according to Leitão, Nunes, and Serrasqueiro (2010), it is not possible to contrast Gibrat's Law based on the growth distribution of the companies, since the use of the quadratic regression methodology, taking as a reference the distribution of the growth of the sample companies as a whole, is appropriate for this purpose. In this manner, the approximation of the distribution of the rates of growth of banking in Brazil in a normal distribution can be seen in Fig. 2. In said figure, it can be observed that there are a greater number of entities with positive growth rates, with most of them being around the central values close to 14% growth.
In this manner, previous studies have presented evidence on how deregulation or an excess of financial regulation influences the variation of the results obtained from the contrast of Gibrat's law (Benito, 2008). This fact presupposes the existence of a non-linear relation between corporate size and growth. Thus, we considered it interesting to carry out a comprehensive analysis of banking growth in case there is a change in the sign of the relation between size and growth.
The quantile regression proposed by Koenker and Bassett (1978) aims to model the existing relation between two variables—a dependent and an independent variable—for different quantiles of the distribution of the dependent variables, and which can be expressed in the following manner:
where yi,t is the dependent variable, x′i,t is the vector of regressors, β is the vector of parameters to estimate, u is the vector of the residues, and Quandθ (yi,t|xi,t) represents the quantile condition θ of yi,t given xi,t. The values that θ can assume are between 0 and 1, using the following expression for its calculation:where ρθ is defined as:In this research, as previously stated, we utilize quartile regressions, which are a particular case of the quantile regressions in which:
Concretely, the multivariate linear model proposed by Goodard et al. (2002) is used to analyze the growth and contrast Gibrat's law, which is expressed as follows:
where Creci,t represents the growth of bank i in year t, which is explained by the size of the entity in the previous year, represented by Tami,t−1, along with a set of control variables that represent profitability, the level of solvency, the percentage of the off-balance sheets, the liquidity rate, and default rate. Finally, βk are the parameters to be estimated and μi,t is the error term.2To guarantee the robustness of the results, the statistic used for the quantile regression is the Pseudo-R2 coefficient, which depends on the estimated quartile (θ) and is expressed through the following equation:
Furthermore, to estimate the parameters of the different quantiles, following Coad and Rao (2008) and Leitão et al. (2010), we used the method of the Bootstrap matrix proposed by Buchinsky (1995,1999) since it is considered to be the most adequate for samples with few observations and mainly due to being valid in the presence of the different forms of heterogeneity.
This methodology is valid to estimate the static linear models, but it is not adequate to estimate dynamic linear models. In that case and according to Powell (2014), the quantile regression for panel data through instrumental variables (QRPD) would be the correct one.
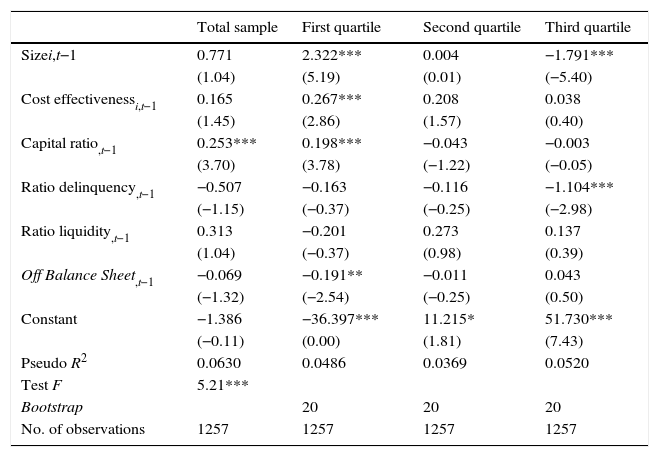
Empirical resultsIn this section, the results obtained from the set of analysis done for the total commercial financial entities that comprise the banking system of Brazil are presented. Concretely, Table 4 shows the results obtained from the contrast of Gibrat's law to examine the relation between the growth and size of commercial banking. Said table presents the results obtained for the total sample and for each of the quartiles. Thus, it is possible to observe that for the set of the sample, the size of the entities does not significantly influence growth. This result implies the acceptance of Gibrat's law, which presupposes that growth is a random process that does not depend on the size of the entities and, therefore, that all entities have the same probability of growth regardless of their size.
Linear contrast of Gibrat's Law. Results for the total sample and per quartile.
| Total sample | First quartile | Second quartile | Third quartile | |
|---|---|---|---|---|
| Sizei,t−1 | 0.771 | 2.322*** | 0.004 | −1.791*** |
| (1.04) | (5.19) | (0.01) | (−5.40) | |
| Cost effectivenessi,t−1 | 0.165 | 0.267*** | 0.208 | 0.038 |
| (1.45) | (2.86) | (1.57) | (0.40) | |
| Capital ratio,t−1 | 0.253*** | 0.198*** | −0.043 | −0.003 |
| (3.70) | (3.78) | (−1.22) | (−0.05) | |
| Ratio delinquency,t−1 | −0.507 | −0.163 | −0.116 | −1.104*** |
| (−1.15) | (−0.37) | (−0.25) | (−2.98) | |
| Ratio liquidity,t−1 | 0.313 | −0.201 | 0.273 | 0.137 |
| (1.04) | (−0.37) | (0.98) | (0.39) | |
| Off Balance Sheet,t−1 | −0.069 | −0.191** | −0.011 | 0.043 |
| (−1.32) | (−2.54) | (−0.25) | (0.50) | |
| Constant | −1.386 | −36.397*** | 11.215* | 51.730*** |
| (−0.11) | (0.00) | (1.81) | (7.43) | |
| Pseudo R2 | 0.0630 | 0.0486 | 0.0369 | 0.0520 |
| Test F | 5.21*** | |||
| Bootstrap | 20 | 20 | 20 | |
| No. of observations | 1257 | 1257 | 1257 | 1257 |
Nota: *, **, *** indican significatividad al 1%, 5% y 10% respectivamente.
However, the results obtained for the different quartiles show that the influence of size on growth varies depending on the quartile that is being analyzed. Concretely, it can be observed that in the first quartile, size has a positive and nonsignificant influence, but in the third quartile the influence is negative and significant.
Regarding the influence of the rest of the variables, the results obtained show that profitability has a positive influence on growth, but it is only significant in the first quartile. The capital ratio also has a positive influence on growth, being significant in the first quartile and in the sample set. On the other hand, the default has a negative and significant influence on the third quartile and the OBS ratio on the first quartile. The results obtained from the tests of good specification show that the variables are significant as a set.
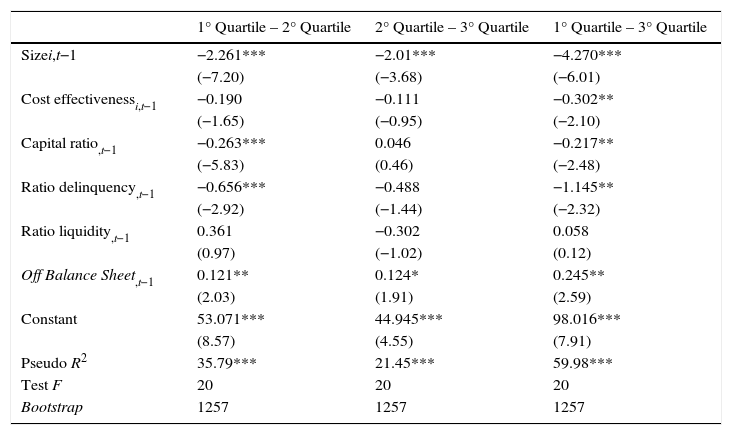
However, Table 5 presents the analysis of interquartile regressions to prove that there are significant differences between the parameters obtained for the different quartiles. Said table shows the results of the interquartile regressions, obtaining that the differences of parameters obtained by quartiles in Table 4 is significant between each of the quartiles for the growth-size relation. These results are corroborated by the significance of the results obtained from the tests of differences of the interquartile parameters.
Differences between interquartile parameters.
| 1° Quartile – 2° Quartile | 2° Quartile – 3° Quartile | 1° Quartile – 3° Quartile | |
|---|---|---|---|
| Sizei,t−1 | −2.261*** | −2.01*** | −4.270*** |
| (−7.20) | (−3.68) | (−6.01) | |
| Cost effectivenessi,t−1 | −0.190 | −0.111 | −0.302** |
| (−1.65) | (−0.95) | (−2.10) | |
| Capital ratio,t−1 | −0.263*** | 0.046 | −0.217** |
| (−5.83) | (0.46) | (−2.48) | |
| Ratio delinquency,t−1 | −0.656*** | −0.488 | −1.145** |
| (−2.92) | (−1.44) | (−2.32) | |
| Ratio liquidity,t−1 | 0.361 | −0.302 | 0.058 |
| (0.97) | (−1.02) | (0.12) | |
| Off Balance Sheet,t−1 | 0.121** | 0.124* | 0.245** |
| (2.03) | (1.91) | (2.59) | |
| Constant | 53.071*** | 44.945*** | 98.016*** |
| (8.57) | (4.55) | (7.91) | |
| Pseudo R2 | 35.79*** | 21.45*** | 59.98*** |
| Test F | 20 | 20 | 20 |
| Bootstrap | 1257 | 1257 | 1257 |
Nota: *, **, *** indican significatividad al 1%, 5% y 10% respectivamente.
Regarding the rest of the variables, it can be observed that the main interquartile differences are produced between the third and the first quartile, with the significant differences being for the variables of profitability, capital, default and OBS ratio. Nevertheless, the first quartile shows significant differences with the second quartile also within the influence of the capital and default ratio.
The results obtained in Table 4 reveal that a non-linear relation between growth and size could exist, since the influence of size on growth changes sign from the first quartile to the third. For this reason, we considered it interesting to contrast the existence of non-linearity between growth and size. To carry out this analysis, we incorporated the quadratic variable of size, expressed by Tami,t−12, into the model proposed by Goodard et al., 2002, leaving the non-linear model as shown below:Creci,t=β0+β1Tami,t−1+β1Tami,t−12+∑i=25βkVCi,t−1+μi,t
Following the previous literature, it is assumed that there is causality between growth and size. Therefore, a possible problem of endogeneity could arise, which needs to be addressed. The instruments utilized to solve the problem of endogeneity will be the delayed explicative variables, since they should have the capacity of providing the information on the explicative variable.
In this manner, the method chosen to obtain robust and efficient estimations is the Generalized Method of Moments (GMM) of differences (Arellano & Bond, 1991), which is a particular instrumental variable method. To show the global significance of the method we present the Wald test expressed through the F-Snedecor. To prove the validity of the instruments the Sargan test for the over-identification of instruments is used. Lastly, the statistical test by Arellano and Bond (1991) is carried out to prove the absence of second order autocorrelation, expressed by m2.
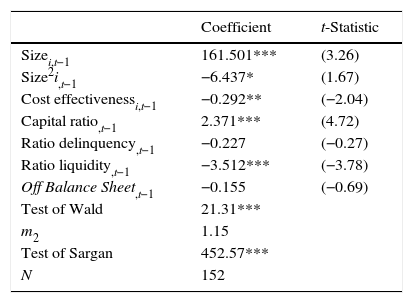
The results obtained in Table 6 corroborate that there is a non-linear relation between size and growth, with the latter being squared in the shape of an inverted U, coinciding with the classical theories that state that smaller companies have a greater growth potential. On the other hand, the results are robust and reliable given that the model is explained as a whole, as indicated by Wald's test. Additionally, there is no second order autocorrelation and the model is not overidentified, as can be observed in the test by Arellano and Bond and by the Sargan test, respectively.
Non-linear contrast of Gibrat's Law.
| Coefficient | t-Statistic | |
|---|---|---|
| Sizei,t−1 | 161.501*** | (3.26) |
| Size2i,t−1 | −6.437* | (1.67) |
| Cost effectivenessi,t−1 | −0.292** | (−2.04) |
| Capital ratio,t−1 | 2.371*** | (4.72) |
| Ratio delinquency,t−1 | −0.227 | (−0.27) |
| Ratio liquidity,t−1 | −3.512*** | (−3.78) |
| Off Balance Sheet,t−1 | −0.155 | (−0.69) |
| Test of Wald | 21.31*** | |
| m2 | 1.15 | |
| Test of Sargan | 452.57*** | |
| N | 152 |
Nota: *, **, *** indican significatividad al 1%, 5% y 10% respectivamente.
Previous empirical evidence on the size-growth relation in the banking sector is not as expansive as in the business sector, especially in emerging economies such as the case of Brazil. However, there are important economic reasons that justify its study such as the important economic growth that this country has experienced in recent years, the importance of the financial sector in its mission to stabilize and support the economic activity of said country, and the strong presence of foreign financial entities, which has also increased since the origin of the international financial crisis.
In this context, this study has aimed to analyze the growth of the financial entities of Brazil during the 2002–2013 period through the contrast of Gibrat's law, considering the start of the period as the year 2002, due to it being the year in which the main regulatory changes of the banking sector in Brazil took place, as well as the liberalization of the sector and the entry of foreign commercial banking. This work has incorporated two new analyses to the growth study, such as contrasting Gibrat's law in the commercial banking of an emerging country, and applying the quartile regressions methodology to said analysis in order to thoroughly analyze the size-growth relation and provide relevant evidence for the construction of a banking growth model that will guide the financial policy of the country.
The results of the work set indicate that there is a complex non-linear relation between size and growth for the set of financial entities that operated in Brazil during the study period. After analyzing more thoroughly the influence of size on growth, we found that size quadratically influences growth, and experiences a change regarding its influence on growth according to the analyzed quartiles. Concretely, we observed that the smaller entities have an expected positive average growth, whereas the entities with a greater volume of assets have a negative growth expectation. These results are especially relevant for the financial authorities of the country, as it allows us to state that in the next years the concentration of the sector will decrease, with the market shares becoming equal among entities.
It would be interesting if future researches analyze the interrelation of growth and profitability in the different emerging economies, contributing to the literature with a greater knowledge of the behavior of the banking sector in these economies. Moreover, due to the influence of the capital, liquidity and diversification ratios of banking business on growth, it would be interesting to analyze the influence of growth on the levels of solvency and liquidity, so that it is possible to examine the influence of commercial banking in the function of stability of the Brazilian financial sector.
Management services of products and instruments derived outside the current operation.
Peer Review under the responsibility of Universidad Nacional Autónoma de México.
Concretely, ui,t=ηi+λt+vk where ηi is the specific error of each unit (unobservable heterogeneity) and which collects those unobservable effects that affect only entity i, λt represents those shocks that occur in moment t and affect all entities equally, and vk is a random disturbance.
This work has received the financial aid of the Junta de Extremadura, concretely of the V Plan Regional de Investigación Desarrollo Tecnológico e Innovación (2014–2017), through the Grupo de Investigación GIMAF (reference GR15027).