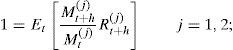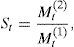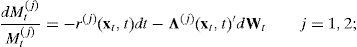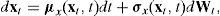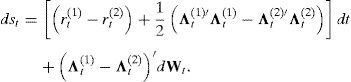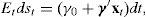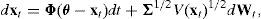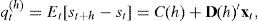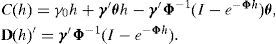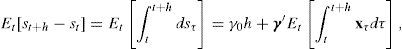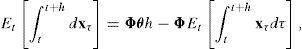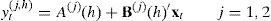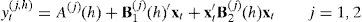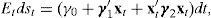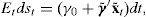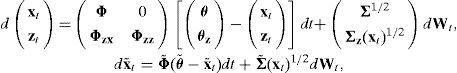This note provides the conditions needed to obtain a multi-country term structure model where both bond yields for each country and the expected rate of depreciation (over any arbitrary period of time) are known affine functions of the set of state variables. In addition, two main families of dynamic term structure models are shown to satisfy these conditions.
The affine term structure model (ATSM), originally proposed by Duffie and Kan (1996), is widely regarded as the cornerstone of modern fixed income theory thanks to its main advantage: tractability. In particular, an ATSM provides analytical expressions for bond yields that are affine functions of some state vector. As noted by Piazzesi (2009), tractability is important because otherwise one would need to compute yields with Monte Carlo methods or solution methods for partial differential equations, which could be especially costly from a computational point of view when model parameters are estimated using data on bond yields.
This note presents a set of conditions that extends the tractability of the single-country ATSM to the multi-country case in the context of international term structure models as those in Backus et al. (2001), Brandt and Santa-Clara (2002) and Brennan and Xia (2006) among others. In particular, this note focuses on internationally affine term structure models where not only bond yields in each one of the countries are known affine functions of a set of state variables, but also the expected rate of depreciation satisfies this property. The main contribution of the present paper is to provide conditions to obtain an expected rate of depreciation (over any arbitrary period of time) that is affine on the set of state variables (Section 2).
Two main families of ATSMs are shown to satisfy these conditions (Section 3). The first subgroup is the so-called completely affine term structure model introduced in Dai and Singleton (2000). However, such a specification has been found empirically restrictive. We overcome this issue by showing that the more flexible class of quadratic-Gaussian term structure models introduced in Ahn et al. (2002) and Leippold and Wu (2003) can also deliver an affine expected rate of depreciation when interpreted as being affine in the original set of variables and their respective squares and cross-products. As shown in Diez de los Rios (2009), these results can be used to estimate ATSMs in a multi-country setting, and to study the exchange rate forecasting ability of such models.
2An affine expected rate of depreciationThe analysis is similar to that in Backus et al. (2001) and Brandt and Santa-Clara (2002). It is based on a two-country world where assets can be denominated in either domestic currency j=1 (i.e., “dollars”) or foreign currency j=2 (i.e., “pounds”). In particular, consider, based on a no-arbitrage argument, the existence of a (strictly positive) stochastic discount factor (SDF), Mt(j), for each country. This SDF prices any traded asset denominated in currency j through the following relationship:
where Rt+h(j) is just the gross h-period return on the asset.In this set-up, the law of one price implies that any foreign asset must be correctly priced by both the domestic and the foreign SDFs which, under complete markets, translates into the fact that the exchange rate St (“currency 1″ per unit of “currency 2″) is uniquely determined by the ratio of the two pricing kernels:
Therefore, one can obtain the law of motion of the (log) exchange rate, st=logSt, using Itô’s lemma on the stochastic processes of Mt(j). To this end, assume the following dynamics of the domestic and foreign SDF:
where rt(j)=r(j)(xt,t) is the instantaneous interest rate (also known as short rate) in country j; Wt is an n-dimensional vector of independent Brownian motions that describes the shocks in this economy; and Λt(j)=Λ(j)(xt,t) is an n-dimensional vector that is usually called the market price of risk because it describes how the SDF responds to the shocks given by Wt. In general, the short rates and the prices of risk are functions of time, t, and a Markovian n-dimensional vector, xt, that describes completely the state of the global economy. The law of motion of these state variables, xt, is given by a diffusion such as:where μx is an n-dimensional vector of drifts, and σx is an n×n state-dependent factor-volatility matrix.Using Itô’s lemma on (3) and subtracting, one gets:
This equation ties the dynamic properties of the exchange rate to the specific parameterization of the drift (interest rates), the diffusion (price of risk) coefficients in (3), and the dynamic evolution of the set of state variables (because interest rates and the prices of risk are ultimately related to those).While the conditions needed to have bond yields in affine form can be found in Duffie and Kan (1996), the following proposition summarizes the conditions needed to get an expected rate of depreciation that is affine in the set of state variables given by xt.
Proposition 1 If the drift of the process that the log exchange rate stfollows is affine in a set of state variablesxt, that is,
Proof First note that the expected rate of depreciation satisfies
The result in this proposition is novel because (to the best of our knowledge) the literature on continuous-time multi-country affine models has focused almost entirely on Euler approximations to the expected rate of depreciation h-periods ahead. For example, Hodrick and Vassalou (2002),Leippold and Wu (2007) and Ahn (2004) use an Euler approximation of the law of motion of the (log) exchange rate to obtain a formulae for the expected rate of depreciation that is valid only for an arbitrary small period h. Yet Eq. (8) has the advantage of being exact and, hence, any model parameter estimates based on this result will not be subject to discretization biases. Similarly, Backus et al. (2001) only provides an expression for the one-period ahead expected rate of depreciation (h=1) and, thus, this proposition generalizes their results to the case of an arbitrary choice of h. For example, Diez de los Rios (2009) exploits Eq. (8) to estimate a two-country ATSM and analyze its forecasting ability when predicting exchange rates up to one year ahead.
Also notice that this proposition states that one can obtain an affine expected rate of depreciation when both the short rates, rt(j), and the instantaneous variances of the pricing kernels, Λt(j)′Λt(j), are affine in xt (which guarantees that the drift of the log exchange rate, st, is affine); and, at the same time, the process that xt follows must be an affine diffusion under the physical measure. Note, however, that these conditions are restrictive with respect to the general class of ATSMs. For example, it is possible to obtain affine bond yields without assuming a model where the instantaneous variance of the SDF is affine in xt (see Duffee, 2002; Cheridito et al., 2007) or without the condition that the state vector must follow an affine diffusion under the physical measure (see Duarte, 2004).
3ExamplesThis section presents additional details on the two main families of ATSMs that belong to the internationally affine class.
3.1Affine models of currency pricingIn this subsection, we focus on a multi-country version of the Dai and Singleton (2000) standard formulation of the ATSMs that nests most of the work on international term structure modelling.1 These models can be considered as multivariate extensions of the Cox et al. (1985) model, and they are characterized by the following set of assumptions:
- 1.
rt(j)=δ0(j)+δ1(j)′xt, where δ0(j) is a scalar, and δ1(j) is an n-dimensional vector.
- 2.
dxt=Φ(θ−xt)dt+Σ1/2V(xt)1/2dWt, where Φ and Σ are n×n matrices, θ is an n-vector, V(xt) is a diagonal n×n matrix with i-th typical element vi(xt)=αi+βi′xt, and Wt is an n-dimensional vector of independent Brownian motions.2
- 3.
Λt(j)=V(xt)1/2λ(j) where λ(j) is an n-dimensional vector.3
Under these assumptions, one can show that bond yields satisfy:
where yt(j,h) is the yield on an h-period zero-coupon bond in country j, and the coefficients A(j)(h)∈R and B(j)(h)∈Rn solve a system of ordinary differential equations whose details can be found in Duffie and Kan (1996) or Piazzesi (2009).Notice that this model satisfies the conditions in Proposition 1, and therefore the expected rate of depreciation h-periods ahead is also an affine function of the state vector xt. Such a formulation is also known as a “completely affine” specification (Duffee, 2002), because it has an instantaneous variance of the SDFs, Λt(j)′Λt(j), that is affine in the set of factors xt. The fact that Et[st+h−st] is also affine adds a new meaning to the term “completely affine specification.” The problem is that such a specification has been found to be empirically restrictive. For example, Duffee (2002) finds that this parameterization produces forecasts of future Treasury yields that are beaten by a random walk specification4; and Backus et al. (2001) point out that this model constrains the relationship between interest rates and the risk premium in such a way that the ability of the model to capture the forward premium puzzle is severely limited. In the next section, we analyze a more flexible family of dynamic term structure models that has been found empirically more plausible.
3.2Quadratic models of currency pricingThe quadratic term structure model was introduced by Ahn et al. (2002) and Leippold and Wu (2003) in order to accommodate rich nonlinear and time-varying dynamics in bond yields. In particular, these models are characterized by the following set of assumptions5:
- 1.
rt(j)=δ0(j)+δ1(j)′xt+xt′δ2(j)xt, where δ0(j) is a scalar, δ1(j) is an n-dimensional vector, and δ2(j) is a symmetric n×n matrix.
- 2.
dxt=Φ(θ−xt)dt+Σ1/2dWt, where Φ and Σ are n×n matrices, θ is an n-vector; and Wt is an n-dimensional vector of independent Brownian motions.
- 3.
Λt(j)=λ0(j)+λ1(j)xt, where λ0(j) is a n-dimensional vector, and λ1(j) is an n×n matrix.
It can be shown that in this framework bond yields have a quadratic form:
where the coefficients for each country j, A(j)(h)∈R, B1(j)(h)∈Rn, and B2(j)(h)∈Rn×n, solve a system of ordinary differential equations. Still, it is possible to view any quadratic model as being affine in the original set of variables and their respective squares and cross-products. To do so, just express (9) as:where x˜t=(xt′,zt′)′ with zt=vech(xtxt′), B˜(j)(h)=B1(j)(h)′,vecB2(j)(h)′Dn′, and Dn is the duplication matrix.6Similarly, it can be shown that the expected rate of depreciation is also affine in this augmented set of factors. To do so, first note that the drift of the (log) exchange rate process can be expressed as:
for some γ0, γ1, and γ2. Second, we can use the same tools as before to show that the drift of the exchange rate is affine in the augmented set of state variables:with x˜t=(xt′,zt′)′ and γ˜={γ1′,[vec(γ2)]′Dn}′. Finally, it can be shown that if one applies Itô’s lemma on zt=vech(xtxt′) then the joint process for xt and zt is an affine diffusion (see Appendix B in Cheng and Scaillet, 2002). In particular, the law of motion of the augmented set of factors x˜t satisfies:where the drift is linear with Φzz=2Dn+(Φ⊗In)Dn,Φzx=−2Dn+(Φθ⊗In), and θz=Φzz−1[vech(Σ)−Φzxθ] and Dn+ being the Moore–Penrose inverse of matrix Dn: Dn+=(Dn′Dn)−1Dn′. In addition, the diffusion term satisfies Σz(xt)1/2=2Dn+(Σ1/2⊗xt), which implies a volatility matrix Σ˜ whose elements are affine in xt and xtxt′ (and, therefore, affine in xt and zt). Therefore, the quadratic model also satisfies the conditions given in Proposition 1 if one interprets this model as being affine in an augmented set of state variables.It is also interesting to note that this quadratic framework also nests the Gaussian essentially affine specification used in Dai and Singleton (2002) and Duffee (2002) when δ2(j)=0 for j=1, 2. Such a model combines Gaussian state variables and an affine market price of risk, and it has been shown to be flexible enough to explain the rejection of the expectations hypothesis of the term structure of interest rates as well as to produce forecasts of future Treasury yields that beat the random walk specification. In this case, bond yields are affine in the set of state variables, while the expected rate of depreciation is quadratic.7
4ConclusionsThis note presents a set of conditions that extends the tractability of the single-country ATSM to the multi-country case. In particular, the main contribution of the present paper is to provide conditions to obtain an expected rate of depreciation that is affine on the set of state variables. As shown in Diez de los Rios (2009), this result can be exploited to estimate ATSMs in a multi-country setting, and to study the exchange rate forecasting ability of such models. Finally, two main families of dynamic term structure models are shown to satisfy these conditions.
The views expressed in this paper are those of the author and do not necessarily reflect those of the Bank of Canada.