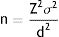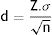For the last few years the p value has been the principal criterion used to define whether one treatment is superior to another. The p value is effectively the probability that the differences found between 2 treatments in a contrast of hypothesis are due to chance and it is assumed that when this probability is lower than .05 (i.e. 5%) the differences between treatments are significant, at least statistically.
The inconvenience of taking a clinical decision solely based on a p value is the lack of clinical correlation of this statistical difference. The main problem is can we mathematically prove that the differences between treatments are not only statistically significant but also clinically significant?
The answer is found in the calculation of the sample size prior to study initiation. The 2 main variables which should be previously defined for a study are the probability of error accepted in judgment by hypothesis (i.e. the α value) and what improvement (or deterioration) of the main value is expected to be obtained with the new treatment y (the c value, or clinical value). Or put another way: what improvement is sufficient for the new treatment to be applied? And what probability of error should be acceptable in the decision?
These 2 variables may be defined prior to the study by using them in estimation of the sample size, in accordance with the conventional formula for quantitative data:
Z is a constant relating to the p, value, i.e. with the probability of error in the judgement which may be accepted (for a α value = .05, the Z value is 1.96 and for a value lower than α, there is a higher Z value), σ is the variance (the square of the standard deviation, i.e. how differently shared is this variable in nature) and d is precision, i.e. What minimal difference would the statistical test be capable of detecting.The power of a statistical test essentially depends on the sample size, and therefore if prior to the beginning of the study, the d value is defined as the clinically significant difference for this study (c value) the test may be provided with the necessary power to observe the difference defined as clinically relevant, not being capable of detecting differences lower than those which are clinically relevant.
If a minor change is made to the formula, we are able to show smaller differences between 2 groups the smaller the value of Z is (greater probability of error), the smaller the standard deviation (a more homogenous behaviour of the variable ) and the greater the sample size (greater test potential).
For this reason, once the α value that one wishes to assume has been defined, the increase in sample size only reduces the magnitude of the difference between two treatments which the test may suggest as statistically significant, but it does not improve the clinical significance of the study. For this reason, when the n value is low, the differences between the groups are of greater clinical relevance.
In one example, a hypothesis contrast may be suggested where we define that preoperative 3D planning reduces times in surgery in primary hip arthroplasty with a significance value of α = .05, a standard deviation between surgical operations of 15 min and a c-value of 30 min. The sample size required to identify these differences if they were real, would be approximately 216 operations. If once this number of operations had been reached the p value was not of significance, it could be said that the 3D impression did not reduce time in surgery in any clinically significant manner. This would not mean that time in surgery was not altered or that there were no statistically significant differences since if the sample size was increased, statistically significant differences would be present, but they would be lower than the c value and therefore would not be clinically significant.
The p value alone has no meaning, it is the compression of the p value which gives criterion to decisions. As far as possible, the contrasts of hypothesis must be previously planned at the beginning of the study and therefore the precision of our contrast of hypothesis (c value) becomes a new tool in planning studies. More accurate judgments may be made and a nexus between statistical significant and clinical significance of a contrast of hypothesis may be established.
Please cite this article as: Ferràs-Tarragó J. El valor c como aproximación entre la clínica y la significación estadísticamente significativa. Rev Esp Cir Ortop Traumatol. 2019;63:381–382.