This study examined social system failures and sought to identify a plausible mechanism behind these failures. Stretched exponential distributions were observed for failure of marriages in the US, UK, and Germany. In addition, the study provides evidence of power laws in the failure of large firms in the US and worldwide. Summation of stretched exponentials leads to power laws, so an underlying principle can be established to link different types of social system failures such as failures of marriages and firms. The generation of these fat-tailed distributions in social system failures can be explained by Zipf's principle of least effort. Therefore, increasing initial efforts at the individual level through marriage counseling or stakeholder synchronization should reduce failures.
Social systems do not last forever (Costanza & Patten, 1995). Whether civilizations, firms, or marriages, their failures have enormous impact on personal and financial stability. Empirical studies have traditionally identified the factors that affect the failure of a social system. However, linking failure patterns across different types of social systems has been a subject of interest for researchers in many disciplines.
Fat-tailed distributions have been empirically observed in numerous natural and social systems, and are most often described in terms of stretched exponentials, log-normals, and power laws. In particular, stretched exponentials have been observed for city sizes (Laherrere & Sornette, 1998); whereas power laws have been identified in human sexual contacts (Liljeros, Edling, Amaral, Stanley, & Åberg, 2001), use of words in languages (Newman, 2005), entry age of marriage (Preston, 1981), as well as for firms regarding their sizes (Axtell, 2001; Gabaix, 2009; Luttmer, 2007), growth (Stanley et al., 1996), and bankruptcy (Fujiwara, 2004; Podobnik, Horvatic, Petersen, Urošević, & Stanley, 2010). Mathematically, a quantity x follows a stretched exponential A·exp(−xβ/τ) by introducing a fractional power law in the exponential function, where β is the stretching exponent ranging between 0<β<1, τ and A are scaling parameters. For power laws a quantity y follows probability distributions of p(y)∝y−α, where α is the scaling parameter and normally lies in the range of 1<α<2 for cumulative distribution functions (CDFs).
Based on revealed empirical patterns of failures for marriages and firms, our study suggests the known least effort principle (Zipf, 1949) as a plausible general mechanism to explain failure of social systems. As the size of social systems depends on the number of individuals interacting (Parsons, 1951), we applied extreme case sampling (Patton, 2005) taking both the minimum number of two individuals required to build a social system (two in marriage), and a very large number of individuals (employees in a blue-chip firm). Therefore, we analyze data of more than 650,000 marriages in the U.S., UK, and Germany for the last 25 years, and about 3250 of the largest firms of the U.S. and worldwide for the last 100, 55, and 15 years. We find CDFs of failure times following stretched exponentials with β≈0.83 in case of marriages and power laws with α≈1.5 for firms. Scale-free power law distributions can result from the summation of fat-tailed distributions by central limit theorem (Stumpf & Porter, 2012; Willinger, Alderson, Doyle, & Li, 2004), which implies that large social systems may fail because of their interacting individuals. Therefore, the best way to reduce the number of divorces and firm failures is to increase the initial efforts of individuals through marriage counseling, or stakeholder synchronization.
The next section presents the material and methods to support our study on failures at marriage (two individuals) level and firm (multiple individuals) level. Subsequently, the results are presented and discussed.
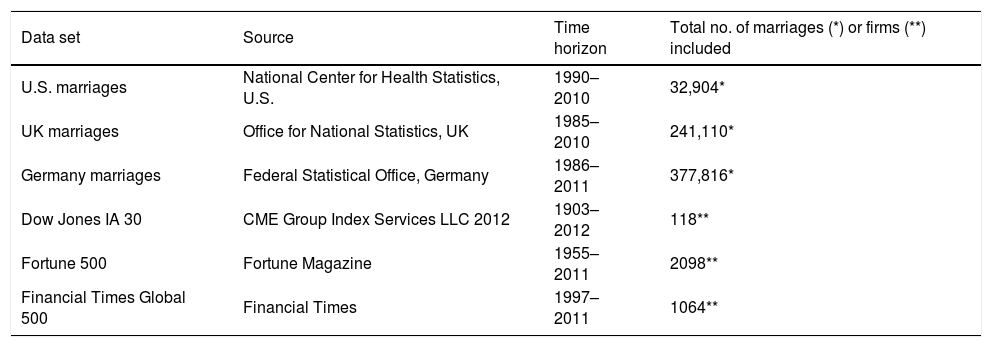
Material and methodsWe analyzed failures of the two social systems: marriages and large firms. Marriage data is derived from panel surveys conducted in the U.S., and divorce records of national courts in the UK and Germany. Firm data includes the largest firms of the U.S. and worldwide taken from a stock index and two popular rankings. As shown in Table 1 (Dow Jones IA 30, 2012; Financial Times Global 500, 2012; Fortune 500 Archive, 2012; Marriages Germany, 2013; Marriages UK, 2013; Marriages U.S., 2012), the used data sets cover hundreds of thousands of marriages and thousands of firms across multiple decades. Recent years include marriages and firms with not yet occurred or unknown failure dates, which skew the data toward the right and result in an overrepresentation of young marriages and young firms. Hence estimated failure rates are upper bounds of the real values (Marriages Germany, 2013; Marriages UK, 2013; Marriages U.S., 2012). In addition to this skewness, U.S. census based marriage data is representative in all demographic dimensions (Marriages U.S., 2012), whereas UK and Germany include the entire divorced population (Marriages Germany, 2013; Marriages UK, 2013). Although firm survival data are subject to many factors, such as industry, booms, or recessions, in this paper we neither distinguish their influences nor control for them, but we do look for a pattern in their combined outcome as measured by firm failures. Additional explanations on the methods used for each data set are given in the results section that follows.
Data set characteristics.
| Data set | Source | Time horizon | Total no. of marriages (*) or firms (**) included |
|---|---|---|---|
| U.S. marriages | National Center for Health Statistics, U.S. | 1990–2010 | 32,904* |
| UK marriages | Office for National Statistics, UK | 1985–2010 | 241,110* |
| Germany marriages | Federal Statistical Office, Germany | 1986–2011 | 377,816* |
| Dow Jones IA 30 | CME Group Index Services LLC 2012 | 1903–2012 | 118** |
| Fortune 500 | Fortune Magazine | 1955–2011 | 2098** |
| Financial Times Global 500 | Financial Times | 1997–2011 | 1064** |
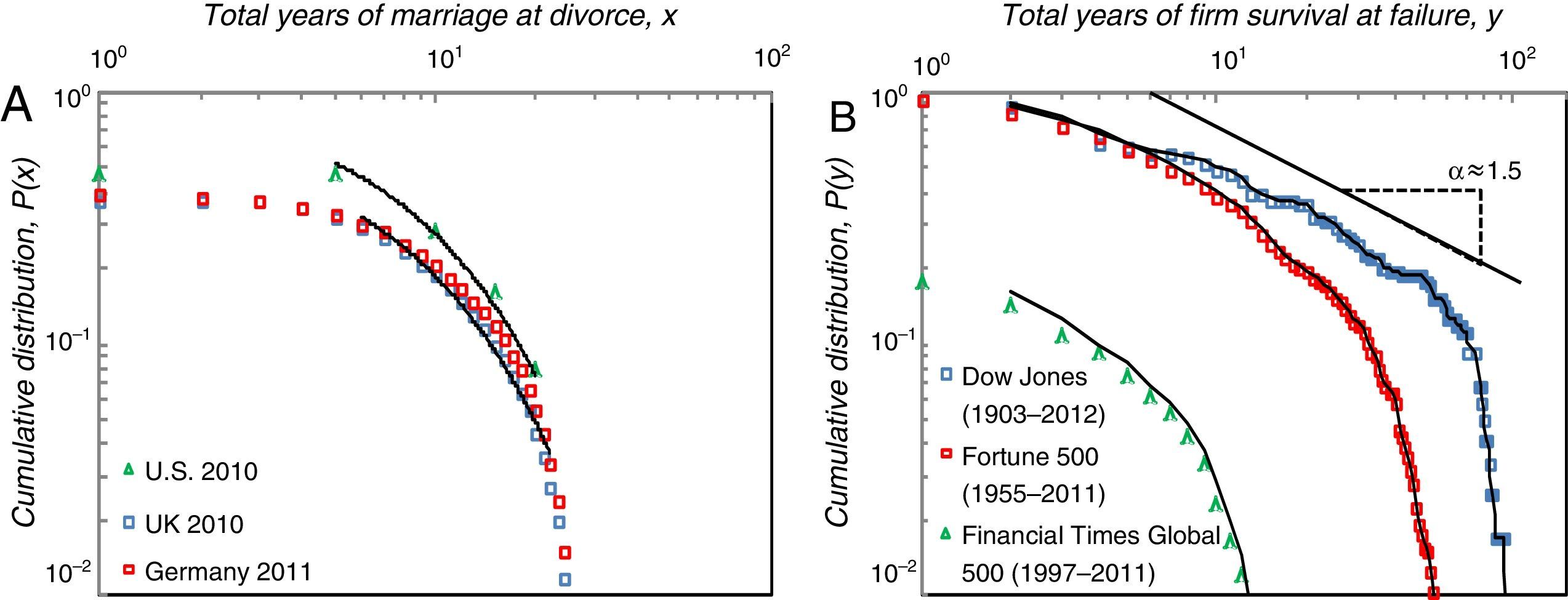
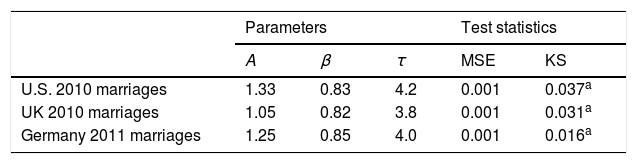
First, to analyze failure distributions for marriages, we looked at frequencies of marriage durations x among all divorces in a given year, normalized by the number of marriages in the corresponding wedding years. By relating each marriage duration to its related marriage cohort, trends like population growth or overall decrease in the number of marriages are equalized. Fig. 1A shows CDFs P(x) for years of marriage at divorce in the U.S., UK, and Germany. Solid lines are best fits to stretched exponential distributions (Laherrere and Sornette, 1998; Podobnik et al., 2010). Average parameter values of high βˆ=0.83 and low τˆ=4 imply that the highest divorce frequencies are around 5–8 years, and approach regular exponential distributions (β=τ=1), as shown in Table 2A. Similar parameters across the countries indicate universal social mechanisms of interaction in marriages. Whereas about 40% of the marriages in Germany and the UK end in divorce within 25 years, almost 50% of marriages in the U.S. end within 20 years, which is consistent with the U.S. Religion and Public Life Survey.
Fig. 1A shows the distribution of total years of marriage at divorce for the U.S., UK, and Germany. CDFs start at the percentage of marriages that survived 20 years (U.S.) or 25 years (UK, Germany) of observation showing about 50% for the first and 60% for the second. Solid lines represent best fit of stretched exponential distributions for each country with average values of βˆ=0.83 and τˆ=4. Initial and late years of marriage excluded from fit due to low frequencies.
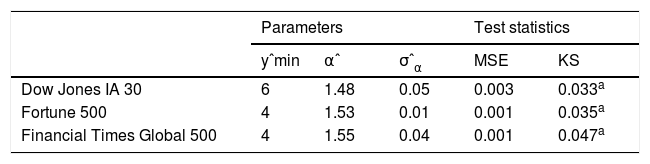
Second, we analyzed firm failure based on firms’ ability to appear year-wise in the Dow Jones IA 30 stock market index, Fortune 500, or Financial Times Global 500 firm rankings. Firm failure has been defined as the inability to stay in a market that combines bankruptcies, mergers, acquisitions, and insignificance due to low revenues or market capitalization (Mitchell, Shaver, & Yeung, 1994; Sinha & Noble, 2008). After cleaning from simple changes of firm names, we derived an appearance matrix including all firms across the years in each of the three longitudinal data sets. Summation of appearances yields pdfs of firm survival, whereupon Fig. 1B shows CDFs P(y) of total years of firm survival in a stock market or ranking at failure. For years yi larger than a specific lower bound ymin, data on a log-log-scale follow a straight line with α≈1.5 indicating power law behavior in the tail, which is consistent with other natural systems showing α-values between 1 and 2. A low α indicates high failure rates, and vice versa. Our α-values suggest highly negative skewed firm failures, where about 40–50% leave the stock index or ranking within the first 10 years. Fig. 1B shows the distribution of total years of firm survival at failure in the respective stock index or ranking. Solid lines are moving averages. As Table 2B shows, all three distributions are roughly linear for yi>ymin for ymin=6 (Dow Jones), and ymin=4 (Fortune 500, Financial Times Global 500) consistent with power law scale free behavior in the tails. Parallelism points toward similar scaling exponents between the stock market index (Dow Jones IA 30 αˆ=1.48±0.05) and firm rankings (Fortune 500 αˆ=1.53±0.01; Financial Times Global 500 αˆ=1.55±0.04). Drops at the very end of the tail are due to finite size effects (Axtell, 2001; Newman, 2005).
Tables 2A and 2B also depict test statistics like MSE, and KS for power law and stretched exponential distributions of the five data sets.
Empirical evidence supports the findings of power law distributions for firm failure (Fujiwara, 2004; Luttmer, 2007; Podobnik et al., 2010) as large social systems, and shows a fit of stretched exponentials for small systems like marriages. Since the summation of stretched exponentials leads to power laws (Stumpf & Porter, 2012; Willinger et al., 2004), and firms consist of many correlated units (Gabaix, Gopikrishnan, Plerou, & Stanley, 2003), the failure at the aggregated level can result from the interplay of small social units. Such interplays in the face of strategic corporate failures have been investigated for boards of directors (Mellahi, 2005) or organizational learning in general (Baumard & Starbuck, 2005).
We propose that fat-tailed distributions of failure result from individuals’ least efforts to maintain a social system. A combination of many factors determines the amount of least effort g(x) an individual puts, i.e., g(x)=attitude (x)+income (x)+trust (x)+···. Since each successful step forward from wedding or firm foundation makes it easier to spend effort due to gained experience such as joint celebrations or brand attractiveness, g(x) is expected to be a monotonically increasing function such that g (x+1)>g(x). Over time, these positive or negative reinforcements become feedback loops, which are a direct condition for fat-tailed distributions, and especially for power laws (Newman, 2005). In addition, the difference between the success and failure of a particular social system could result from individual beliefs about the survival of the marriage or firm in the future, which determines the direction of putting in the least amount of effort.
ConclusionsWe found strong empirical patterns for marriage and large firm failure across the U.S., UK, and Germany. Failure rates of more than 40% for marriages or 90% for firms across a few decades exemplify fat-tailed probability distributions result from transient dependency of events, in contrast to the common belief of Gaussian ones. Recognizing the ubiquity of power laws in large social systems’ failure with characteristic parameters for the U.S. and worldwide could be extended toward patterns of instability of financial markets (Gabaix et al., 2003) or analyzing other social systems of different magnitude. Moreover, our findings can simplify and motivate subsequent analysis of mechanisms for generating power laws from aggregation of fat-tailed distributions (Stumpf & Porter, 2012; Willinger et al., 2004). Initial success allows individuals to gain experience, and leads to reduced efforts by positive reinforcement i.e., growth and underinvestment. Therefore, increasing personal awareness of mature partner selection or periodic counseling by family members to offer moral support during trouble phase of marriage and gradually bringing change in family culture and thinking (e.g., Welsh, Memili, & Kaciak, 2016) can reduce the number of divorces. Likewise, stakeholder selection and extended board meetings for reinforcing dynamic capabilities of firms (Burisch & Wohlgemuth, 2016) and knowledge creation through strategic alliances (Bouncken, Pesch, & Reuschl, 2016) can help to reduce early failures of firms. Nevertheless, the ties in a social system are susceptible to the volatility of human relationships.