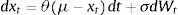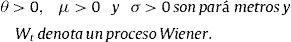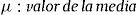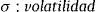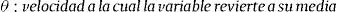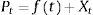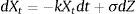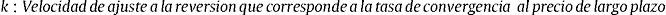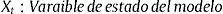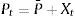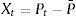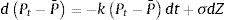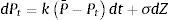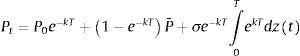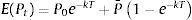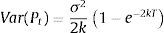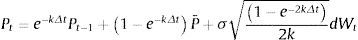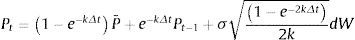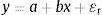La presente investigación tiene como objetivo principal desarrollar un análisis de toma de decisiones bajo incertidumbre a través de la aplicación de opciones reales en la evaluación de inversiones en proyectos mineros. Asimismo, se propone estudiar el comportamiento de los precios del oro, para el caso específico de Perú, utilizando precios históricos y en base a procesos de precios de commodities. Para ello se ha utilizado el modelo Ornstein-Uhlenbeck.
El principal resultado es que evaluar proyectos mediante el enfoque de opciones reales permite valorizar —en su real magnitud— los beneficios económicos asociados a un proyecto de inversión, debido a que se tiene en cuenta el trinomio rentabilidad-riesgo-flexibilidad. La metodología de valorización a través de opciones reales posibilita estructurar el pensamiento estratégico.
This study has as its main objective to develop an analysis of decision making under uncertainty using the real options application in the evaluation of investments in mining projects. It is also proposed to study the behaviour of gold prices, for the specific case of Peru, using historic prices and based on the commodity prices process. The Ornstein-Uhlenbeck model has been used for this.
The main result is that to evaluate projects using the real options approach allows to evaluate –in their real magnitude– the financial benefits associated with an investment project, as it takes into account the trinomial of profitability-risk-flexibility. The assessment method using real options makes it possible to structure strategic thinking.
La presente investigación está orientada a evaluar y valorizar la opción de cierre temporal de una mina de oro bajo condiciones de incertidumbre. Se pretende estructurar una metodología que integre aplicaciones de opciones reales con modelos de precios de commodities basados en procesos estocásticos1. Además, se busca desarrollar un esquema metodológico de apoyo para la toma de decisiones en la asignación de capital para inversionistas en proyectos, específicamente en los mineros auríferos.
Para el análisis empírico se utiliza el modelo Ornstein-Uhlenbeck, que incorpora tanto el proceso de reversión a la media como el movimiento browniano. Para esto, se han tomado datos de precios históricos del oro, de forma mensual, durante el período comprendido entre enero de 2000 y junio de 2012.
El análisis de los resultados revela que la flexibilidad en las decisiones agrega valor al proyecto cuando existe volatilidad en el comportamiento de los precios o en presencia de elevada incertidumbre. Finalmente, se demuestra que el análisis de opciones reales logra entregar una visión diferente que sirve de apoyo en la toma de decisiones de inversión, en este caso en proyectos mineros auríferos.
2Marco teóricoLa literatura en el área de las opciones reales es relativamente reciente. Sus orígenes provienen de la teoría financiera de valoración de opciones, que se inició con el trabajo pionero de Black y Scholes (1973), Merton y Robert (1973), Cox y Ross (1976) y Cox, Ross y Rubinstein (1979).
Así, por primera vez, Brennan y Schwartz (1985) evaluaron un proyecto de recursos naturales a través de los modelos de Black, Scholes y Merton. Ellos sabían que los recursos naturales tienen un alto grado de incertidumbre en fijación de precios. La técnica fundamental en la teoría de opciones reales se basa en la teoría del arbitraje. Brenan y Schwartz (1985) evaluaron una mina de cobre, considerando las opciones de apertura, cierre y abandono de las operaciones. En su trabajo tuvieron en cuenta los costos asociados a la apertura, cierre y mantenimiento de una mina cerrada. El precio del activo de salida (cobre) se modeló como una variable estocástica que sigue un proceso geométrico browniano, y la política óptima está dada por tres precios críticos.
McDonald y Siegel (1985) estudiaron la situación que enfrenta una empresa cuando debe decidir invertir en proyectos riesgosos. En este caso, se asume que la firma puede detener temporalmente su producción si la variable estocástica que modela los costos excede las ventas. Los autores asumen que los individuos que manejan la empresa son adversos al riesgo.
Por su parte, Trigeorgis y Mason (1987) proporcionaron diversos ejemplos de valorización con opciones reales en diferentes tipos de proyectos. Así demostraron que las opciones de diferir, expandir o cerrar proyectos de recursos naturales dependen significativamente de las fluctuaciones de los precios de los commodities.
Después de Brenan y Schwartz (1985), Mardones (1993) utilizó la teoría de opciones financieras como una aplicación del Análisis de Créditos Contingentes (CCA, por sus siglas en inglés) o Valorización de Activos Derivados (DAV) para obtener el valor agregado, a través de la flexibilidad, de un proyecto de cobre en Chile. En 1996 se dio a conocer la Valorización Moderna de Activos (MAP) o Valorización de Opciones (OP), método utilizado para analizar la estructura financiera de empresas mineras. Estas técnicas permitieron llevar a cabo análisis más precisos del tiempo, incertidumbre, y estructura del proyecto. Hoy en día, MAP u OP son conocidas dentro de la literatura financiera como ROV (Teoría de Opciones Reales).
Berger, Ofek y Swary (1996) examinaron la opción de abandono de una compañía minera, postulando que este tipo de opción añade valor a la empresa. Otras investigaciones aplicadas a la teoría de opciones reales en recursos naturales, minería, petróleo y gas, como las realizadas por Kulatilaka y Marcus (1992), Laughton y Jacoby (1993), Mauer y Ott (1995), Palm y Pearson (1986), concluyen en que las opciones de aplazar, modificar, cambiar y cerrar los proyectos aumentan su valor.
Schwartz (1997), compara tres modelos de comportamiento estocástico de los precios de las materias primas, teniendo en cuenta la reversión a la media. El primer modelo plantea un proceso con reversión a la media del tipo Ornstein-Uhlenbeck para el logaritmo del precio spot. El segundo modelo tiene en cuenta otro factor estocástico, el rendimiento de conveniencia (convenience yield), que se supone que sigue también un proceso de reversión media. Por último, el tercer modelo incluye, además, las tasas de interés. El análisis revela una fuerte reversión a la media en los precios de los commodities.
3MetodologíaUna de las metodologías tradicionales de valorización es el análisis del flujo de caja descontado (FCD); es relativamente simple, ya que predice una corriente de flujos de fondos, que son pagados y cobrados durante la vida probable de un proyecto y se descuentan a una tasa de interés determinada —habitualmente el costo promedio ponderado de capital (WACC, por sus siglas en inglés)— que refleja tanto el valor del dinero en términos de tiempo como el grado de riesgo de esos flujos de fondos. El valor temporal del dinero indica que el dinero que se tenga en el futuro vale menos que el que se tiene hoy porque —a diferencia del dinero futuro— el que se dispone hoy puede ser invertido para generar intereses. Uno de los resultados de esta metodología es el valor actual neto, que mide la creación de valor de la inversión. Así, un proyecto con Valor Actual Neto positivo (VAN>0) creará valor y, por lo tanto, debería seleccionarse.
A diferencia del método FCD, la técnica ROV puede funcionar mejor en situaciones con alto grado de incertidumbre. También asume que los directivos de las compañías tienen la flexibilidad para adaptar y revisar las decisiones futuras en respuesta a las circunstancias cambiantes. La incertidumbre se convierte en otro componente del problema a manejar. El futuro es considerado lleno de alternativas y opciones, que pueden agregar valor en sendos casos.
La técnica de aplicar opciones reales a la evaluación de proyectos incluye factores que la metodología clásica —en algunos casos— ha dejado de lado, tales como la flexibilidad, la incertidumbre y la volatilidad. A través de la inclusión de estos componentes se puede llegar a un análisis mucho más dinámico, que permita vincular el proyecto con el panorama económico, estratégico y de mercado logrando, mediante herramientas financieras y estadísticas, flujos de caja futuros mucho más acordes con la realidad del mismo.
La valoración de las opciones reales aplica el pensamiento que subyace a las opciones financieras para evaluar activos físicos o reales. Por analogía con una opción financiera, una opción real es el derecho pero no la obligación de adoptar una acción que afecta a un activo físico o real, a un costo preestablecido, durante un lapso predeterminado (la duración de la opción). Si bien las opciones reales y financieras tienen muchas semejanzas, la analogía no es exacta.
El enfoque de opciones reales parte del reconocimiento del papel importante que la gestión dinámica y continuada de los proyectos de inversión juega en la determinación de su valor; y, por tanto, en el análisis de su aceptación o rechazo. La técnica ROV permite que los directivos evalúen las opciones reales para agregar valor a sus empresas, proveyéndoles una herramienta para reconocer y actuar ante nuevas oportunidades con el objeto de aumentar las ganancias o mitigar las pérdidas. Si bien muchos directores no están acostumbrados a evaluar opciones reales, sí están familiarizados con el concepto de intangibles del proyecto. La técnica ROV ofrece a los directivos empresariales una herramienta para trasladar algunos de esos intangibles a un ámbito en el que puedan ser abordados en forma tangible y coherente.
Un parámetro fundamental en la evaluación de proyectos mediante opciones reales es la volatilidad. Los modelos de opciones reales requieren de la volatilidad, y esta no es fácil de calcular, dado que usualmente no existe información histórica del activo subyacente. Para estimar la volatilidad, algunos autores han empleado métodos basándose en la simulación de Montecarlo.
Así, Copeland y Antikarov (2001), proponen un modelo general para la estimación de la volatilidad en la evaluación de proyectos a través del uso de la simulación de Montecarlo. Este método de cálculo es el más recomendado y utilizado por autores como Herath y Park (2002), Munn (2002), Cobb y Charnes (2004), entre otros.
4Aplicación del modelo Ornstein-Uhlenbeck y estimación de flujos de caja descontados. Estimación de ingresos y egresos4.1Estimación de ingresos4.1.1Modelos de precios de commoditiesEl desarrollo de modelos de comportamiento de precios spot de commodities se basa en procesos estocásticos que se pueden clasificar según dos características: la estacionariedad o no de los modelos y el número de factores estocásticos utilizados (Milla, 2005). Un modelo estacionario se refiere a un proceso donde las propiedades estadísticas son constantes sobre períodos largos de tiempo; es decir, las perturbaciones son transitorias y no afectan el comportamiento de largo plazo de la variable. En cambio, en un proceso no estacionario las propiedades estadísticas de la variable no son constantes y cambian en el tiempo según el nivel de las perturbaciones del proceso. La mayor parte de los modelos desarrollados para precios de commodities son no estacionarios, lo que evidencia la necesidad de trabajar con modelos que caractericen de forma más realista el comportamiento de los precios.
El número de factores estocásticos o variables de estado utilizados para caracterizar la dinámica de los precios de commodities depende de las características del activo analizado. En general, a mayor número de factores, más realista es la modelación; pero con ello aumenta el nivel de complejidad de los procesos involucrados.
Uno de los primeros trabajos en caracterizar el comportamiento del precio de un commodity es el de Brenan y Schwartz (1985), donde se modela el precio del cobre a través de un movimiento browniano geométrico2 que es un proceso de un solo factor estocástico. La evidencia empírica e investigaciones ulteriores reconocen la presencia de una tendencia de largo plazo en los precios de commodities, relacionada con los costos marginales de producción de dichos activos. Gibson y Schwartz (1990) desarrollan un modelo de dos factores estocásticos, donde el precio spot del petróleo sigue un movimiento browniano geométrico y el retorno por conveniencia a un proceso con reversión a la media del tipo Ornstein-Uhlenbeck. Luego, Schwartz (1997) extiende el modelo con un tercer factor estocástico que representa el precio medio de largo plazo a través de otro proceso con reversión a la media.
El trabajo de Schwartz y Smith (2000) presenta un modelo de dos factores estocásticos, incluyendo un factor de reversión a la media que permite modelar las fluctuaciones de corto plazo del precio spot de un commodity y un factor de equilibrio que captura la dinámica de largo plazo de los precios. En Cortázar y Schwartz (2003) se implementa un modelo de factores para el precio futuro del petróleo, siendo más simple y parsimonioso que sus antecesores en la forma de estimar los parámetros de los datos de mercados de futuros.
Otro enfoque para el análisis de precios de commodities consiste en modelar directamente los precios de los contratos futuros o forwards transados en los mercados, construyendo curvas aproximadas de precios —basándose en la metodología Heath-Jarrow-Morton (HJM) propuesta en el trabajo de Heath, Jarrow y Morton (1992)—. Bajo este esquema de análisis, se describe la dinámica temporal de las curvas de precios forward utilizando procesos brownianos multidimensionales para las variables de estado. El estudio de Manoliu y Tompaidis (2002) presenta un modelo de dos factores para el precio de contratos futuros de un commodity energético, utilizando datos de series de precios futuros de gas natural; incluye una variable de estado determinística para modelar la estacionalidad del comportamiento de los precios.
4.2El modelo de Ornstein-UhlenbeckFue propuesto por Ornstein y Uhlenbeck (1930), para modelar la velocidad del movimiento difuso de una partícula en intervalos de tiempo pequeños. Luego de un choque, una partícula no se detiene después de cambiar de posición, moviéndose de forma continua a medida que pierde velocidad. A diferencia de un simple movimiento browniano, el modelo Ornstein-Uhlenbeck sí es capaz de capturar esta pérdida de velocidad.
Se trata de un proceso estocástico que, en términos generales, describe la velocidad de una partícula browniana bajo la influencia de una fricción. El modelo es estacionario, Gaussiano y Markov, y es el único que satisface estas tres condiciones, lo que permite las transformaciones lineales de las variables en espacio y tiempo. Con el tiempo, tiende a inclinarse hacia su media de largo plazo, como un proceso de reversión a la media. Puede ser considerado como una modificación de un recorrido aleatorio (random walk) en tiempo continuo, o proceso de Wiener, donde las propiedades del proceso han sido cambiadas; de modo que hay una tendencia por la que el recorrido se mueve hacia una posición central, con una mayor atracción cuando el proceso está más lejos del centro. El proceso de Ornstein-Uhlenbeck también puede considerarse análogo al de tiempo discreto AR(1)
Lucía y Schwartz (2002) proponen una versión del modelo Ornstein-Uhlenbeck que ha sido utilizada en valorización de opciones en posteriores investigaciones, como en este caso. El modelo caracteriza el precio spot a través de dos componentes (véase la tabla 2). El primero se considera totalmente predecible y se representa como una función determinística conocida dependiente del tiempo f(t); este componente caracteriza la regularidad en la evolución de los precios como alguna tendencia determinística o comportamiento periódico. El segundo término es un proceso estocástico estacionario con reversión a la media del tipo Ornstein-Uhlenbeck Xt.
La naturaleza de las series históricas del precio del oro evidentemente es discreta; por lo tanto, el proceso continuo debe ser discretizado para poder estimar sus parámetros. La ecuación incluye una función determinística f(t), que se fija como la tendencia de largo plazo del precio P que representa el nivel medio histórico en el modelo. Así, el proceso continuo de precios de un factor estocástico puede ser representado como:
Esto significa que hay una fuerza de reversión sobre la variable P, que hace que converja hacia un nivel de equilibrio P¯. La velocidad del proceso de reversión está dada por el parámetro k. Esta ecuación diferencial estocástica posee una solución en términos de la integral estocástica (Integral de Ito):
La variable Pt tiene distribución normal con las siguientes expresiones para la media y la varianza:
La ecuación del valor esperado de la media de Pt es simplemente un promedio ponderado entre el nivel inicial P0 y el nivel de largo plazo P¯ (los pesos suman uno y son funciones del tiempo y la velocidad de reversión). Existe la siguiente relación entre la velocidad de reversión a la media (k) y la vida media (H) del proceso: H=ln(2)/k. La vida media (H) es el tiempo esperado por el cual la variable regresa hacia su valor de medio de largo plazo P¯.
Para realizar la simulación es necesario obtener la ecuación de tiempo discreto para este proceso. El formato correcto de tiempo discreto para el proceso de tiempo continuo de reversión a la media es el proceso estacionario autorregresivo de primer orden, AR(1). Por lo que la ecuación de simulación para P(t) se realiza utilizando la expresión de tiempo discreto, (válido para cualquier tamaño de Δt):
La ecuación anterior puede verse como la suma de la ecuación de valor esperado con un término aleatorio (aparece la distribución normal estándar) con media cero. La discretización del AR(1), presentada en la ecuación descrita líneas arriba, es exacta en el sentido de que podemos utilizar Δt grandes, sin ningún problema en cuanto a la exactitud de la simulación. Así, P(t) tiene distribución normal y puede asumir valores incluso negativos. En muchas aplicaciones deseamos que la variable estocástica asuma solo valores positivos, por ejemplo, en el caso de los precios de los productos, P.
Los parámetros k, σ y P¯ se han estimado a través de un modelo OLS. Para realizar los cálculos se han utilizado datos de precios históricos del oro desde el año 2000 hasta 2012. Reordenando la ecuación previa3 tenemos que:
Los valores encontrados para cada parámetro son coherentes con investigaciones previas como, por ejemplo, Brenan y Schwartz (1985). La velocidad de reversión para el oro no es comparable con otros commodities, pues es mucho más lenta que cualquier otro metal, aunque resulta ser muy volátil.
4.3Modelo Ornstein-Uhlenbeck: aplicación empíricaDebido a que en la actualidad no existe consenso sobre las perspectivas de crecimiento del precio del oro, se han tomado dos posibles escenarios para poder estimar el comportamiento del mismo: uno alcista y otro bajista. Para ambos escenarios, el producto del precio por la cantidad de oro extraída proporciona el valor de los ingresos. Se considera que todo lo que se produce se vende.
4.4Producción de onzas de oroLa minería peruana enfrenta uno de sus años más difíciles tras un largo período de auge. Se estima que la producción del sector caería en 2012 por tercer año consecutivo; los precios continúan cediendo por la desaceleración económica global, las reservas de oro siguen a la baja y los conflictos sociales amenazan paralizar gigantescos proyectos. En los últimos años, los altos precios de los metales han amortiguado la caída en la producción de metales, pero la crisis de deuda europea presionó el valor de las exportaciones mineras. Debido a esto, se ha proyectado la cantidad de mineral producido con una variación de -4% (Diario GESTIÓN, 2012).
4.5Escenario alcistaDada la situación económico-financiera mundial, los análisis de especialistas en la materia divergen en sus pronósticos con respecto al precio del oro: algunos creen que su tendencia seguirá siendo al alza, mientras otros consideran que habría que realizar correcciones a la baja.
Según Bernhard Schmidt4, la clave para entender la fortaleza del oro es que este atraviesa un proceso por recuperar su condición de dinero. En otras palabras, el oro se encuentra en un momento de remonetización como consecuencia de la pérdida de confianza en el papel moneda. La creación masiva de liquidez y las tasas de intereses reales mínimos —o incluso negativos— son los dos promotores más importantes para el oro.
En contra de lo que muchas personas piensan, todavía no existe una “euforia” del oro; mientras en 1980 el sector aurífero representaba más del 26% del patrimonio financiero mundial (renta fija y renta variable), hoy en día no llega siquiera al 5%, lo que reafirma la frase de que “muchos hablan del oro pero pocos lo tienen en sus bolsillos”.
A pesar de la debilidad del oro en los últimos meses, los vendedores de este metal hablan de una demanda muy fuerte y a menudo se les agota el stock, lo que muestra la diferencia entre el precio del “oro papel” que cotiza en la bolsa y la situación real del oro físico. Schmidt opina que el oro seguirá su tendencia alcista en 2012 y las empresas auríferas se recuperarán. Los pronósticos en un mercado irracional, manipulado y volátil son difíciles, pero cree que el oro no llegará en 2012 por debajo de 1 450 dólares, y cotizará finalmente entre 1 800 y 2 000 dólares, si se mantiene el sistema estable. Además, sostiene que si la confianza en el euro y otras divisas de papel moneda, tanto como la solvencia de los grandes estados y del sector bancario se desploman, el precio del oro debería subir muy por encima de los 2 000 dólares.
Por otro lado, la revisión de Basilea III puede revitalizar el rally del oro, si finalmente aquella decide en su nueva consideración de las normas calificar el oro como activo tier 15, reconociéndolo como dinero real, según asegura Peter Krauth, en moneymorning.com.
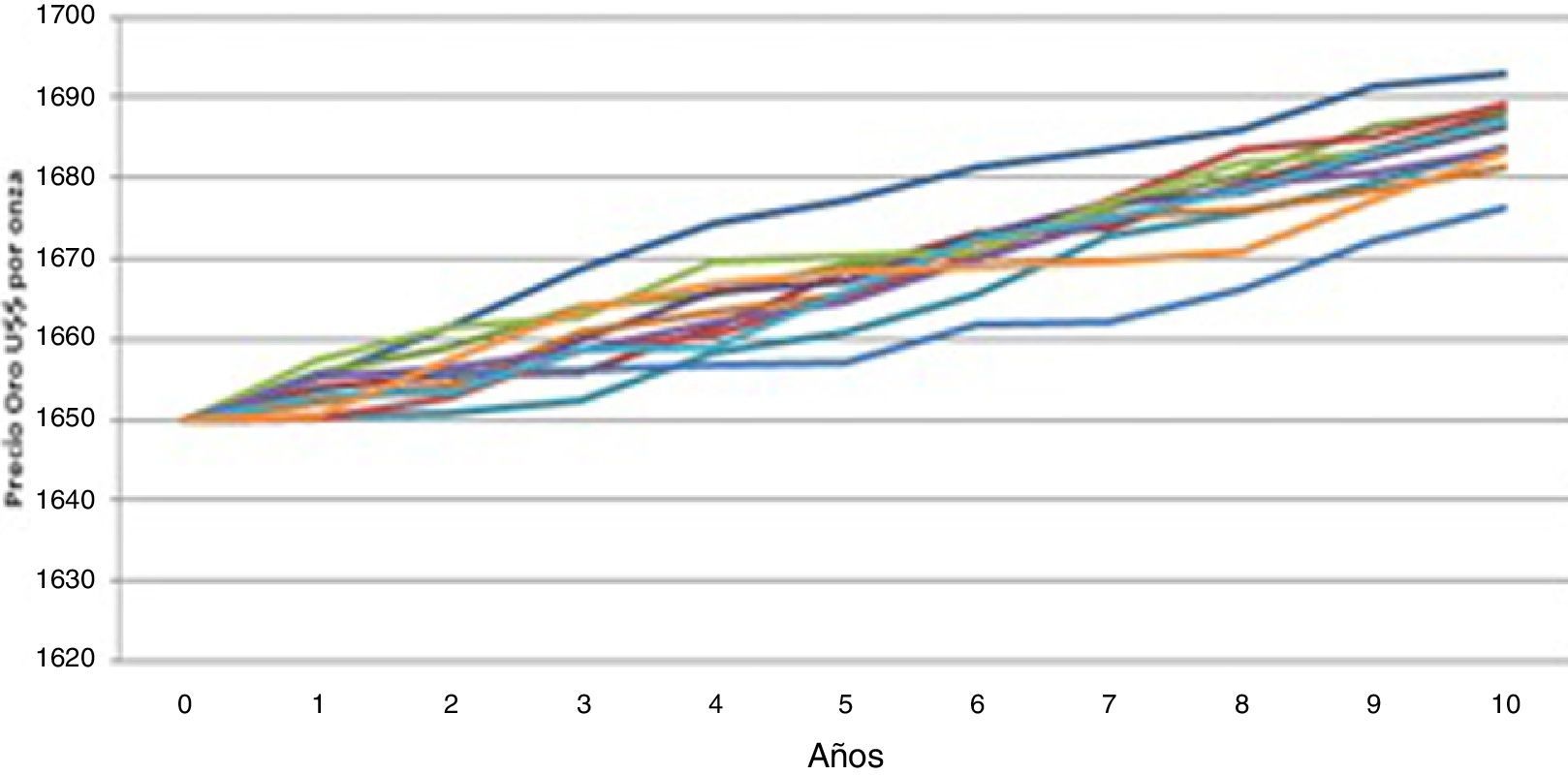
Sobre esta base, y para poder realizar las estimaciones necesarias, se ha tomado como precio medio US$ 2 000. En la figura 1 se muestran algunas simulaciones considerando el escenario alcista.
Escenario alcista.
Modelo continuo.
Simulación de sendas del precio de oro.
Fuente: www.kitco.com.
Las sendas obtenidas al utilizar la forma continua son como aparecen en la figura 1. El gráfico muestra que con un precio inicial de US$ 1 650 por onza troy y con un precio medio de US$ 2 000 por onza, las sendas empezarán a crecer durante los próximos diez años, pero de manera lenta. Se estima que para que el oro llegue a su valor medio histórico pasarán, al menos, 31 años6.
4.6Escenario bajistaEntre aquellos que han realizado revisiones a la baja se encuentra el banco suizo Credit Suisse, que adhiere a una serie de bancos internacionales que han rebajado su pronóstico sobre los precios de los metales preciosos para los años 2012 y 2013, en medio de la incertidumbre sobre el crecimiento mundial (Oro y Finanzas, 2012).
El gigante de la banca suiza ha realizado sustanciales recortes en sus pronósticos de precios de metales básicos, siendo más moderado en su reducción de las perspectivas sobre metales preciosos como el oro. Credit Suisse prevé un precio medio de 1 680 dólares la onza para 2012, esto es un 5% menos que sus estimaciones previas. Para 2013, calcula un precio medio del oro en 1 720 dólares la onza, un 4.2% por debajo de la estimación anterior.
Asimismo, en un informe publicado recientemente, la entidad financiera estadounidense Morgan Stanley ha rebajado su pronóstico para el precio de la mayoría de los metales preciosos e industriales hasta 2014. Como señala el informe del banco7, en los últimos meses las materias primas como activos de inversión han tenido que enfrentar la fortaleza del dólar, la ralentización del crecimiento de la economía mundial y el aumento a la aversión al riesgo.
Peter Richardson y Joel Crane, analistas de Morgan Stanley, muestran optimismo sobre las perspectivas del oro pero, a pesar de todo, reducen sus expectativas para el precio del metal. Así, rebajan su estimación promedio a 1 677 dólares por onza troy para 2012, a 1 816 en 2013 y a 1 760 para 2014.
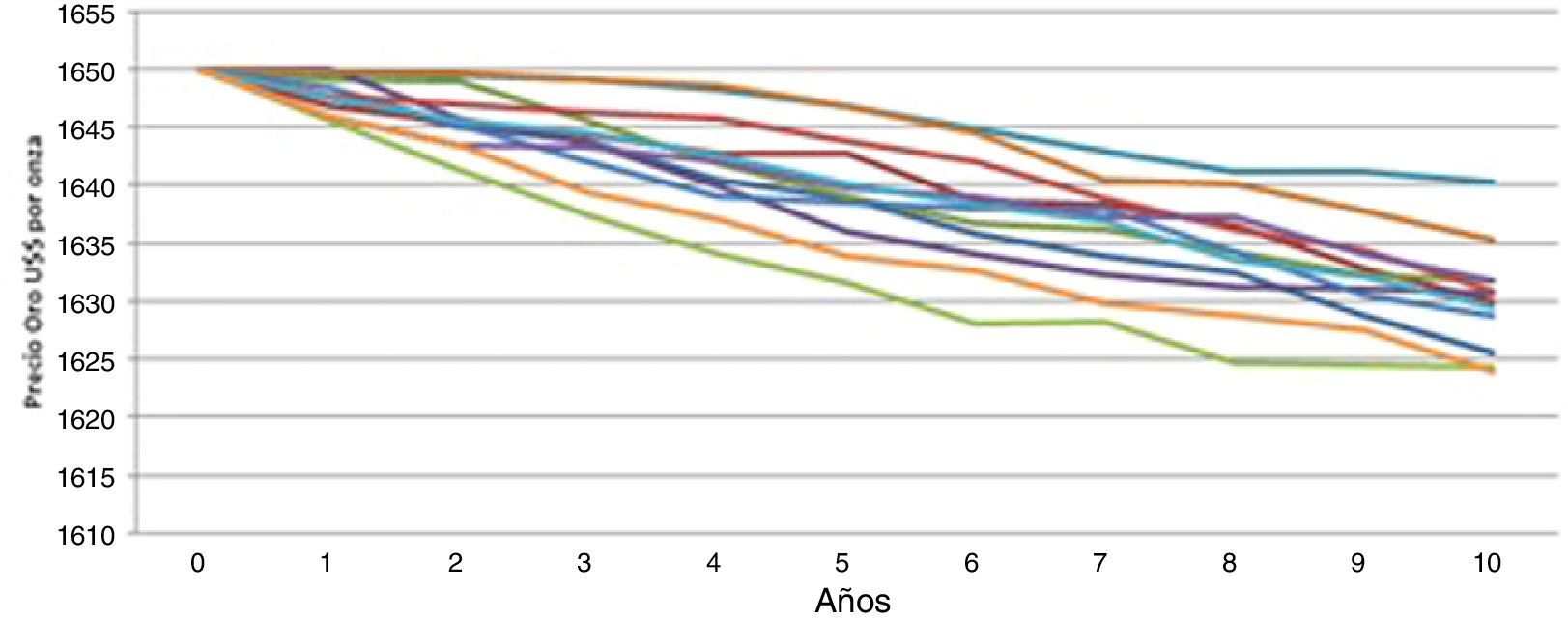
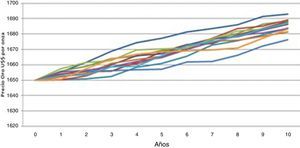
En base a lo antes descrito y para poder realizar las estimaciones necesarias, se ha tomado como precio medio US$ 1 450. En la figura 2 se muestran algunas sendas estimadas para este escenario.
Escenario bajista.
Modelo continuo.
Simulación de sendas del precio de oro.
Fuente: www.kitco.com.
Para estimar los egresos, se ha tomado como referencia la información publicada por la Compañía Minera Poderosa SA8, empresa aurífera subterránea de mediana minería ubicada en el distrito y la provincia de Pataz, a casi 320 kilómetros de la ciudad de Trujillo, en la región La Libertad, Perú.
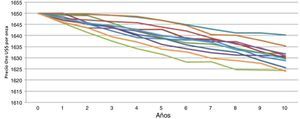
Considerando datos históricos de los estados financieros de la empresa, se han proyectado flujos de caja con y sin opción de cierre temporal. Para esto, se consideró lo siguiente:
Ebitt: Utilidad antes de intereses e impuestos en el período t.
Dept: Depreciación del período t.
Δ CTt: Inversión en capital de trabajo.
Δ Invt: Inversión en el período T.
t: Tasa impositiva efectiva para la empresa.
El capital de trabajo se ha tomado como la diferencia entre al activo corriente operativo y el pasivo corriente operativo. El EBIT se ha expresado como un porcentaje promedio, basado en datos históricos: EBIT/ventas. En cuanto a la depreciación, se considera que varía a una tasa anual de 18.5%. Las inversiones fueron proyectadas a partir de cada uno de sus componentes: obras en curso, cierre de minas, exploración y desarrollo y activos fijos.
Considerando datos históricos, se han proyectado los costos de ventas, siendo el 70% de estos para costos de ventas fijos y el 30% para costos de ventas variables. La proyección de los gastos operacionales se ha realizado en base a los gastos por exploración y desarrollo, gastos administrativos y gastos de ventas. Para cada uno de ellos se ha establecido un porcentaje para gastos fijos y para gastos variables. Asimismo, para determinar los gastos fijos se han considerado cargas de personal y tributos, y para los gastos variables cargas diversas de gestión, servicios prestados a terceros y consumo de suministros.
Finalmente, los costos de cierre, de mantenimiento y de apertura se han considerado depreciables, debido a la imposibilidad de realizar una estimación de los mismos, pese a consultar diversas fuentes relacionadas con el sector.
5Resultados5.1Cálculo del valor de la opción de cierre temporalEn cierto tipo de industrias —como las de extracción de recursos naturales (minería, petróleo, gas, entre otros), de generación de energía eléctrica o en la planificación y construcción de industrias cíclicas (moda, bienes de consumo, entre otras)— existe la posibilidad de detener temporalmente la totalidad del proceso productivo cuando los ingresos obtenidos son insuficientes para hacer frente a los costos, y volver a producir cuando la situación se haya revertido.
Por supuesto, el análisis se puede extender a una serie de cierres y reaperturas según el precio sea inferior o superior a los costes variables; pero, en este caso, se debe considerar que el precio ascienda por encima de una cantidad determinada sobre el coste variable antes de reiniciar la producción, con el fin de minimizar el riesgo de que se produzca una pérdida y hacer frente a los costes de reapertura.
5.2La opción de cierre temporalSi en un período de tiempo el precio del oro cayera haciendo que el flujo de caja sea negativo, podría ser recomendable cerrar la mina hasta que los precios suban. Sin embargo, si se cierra la mina, aún se tendrá el flujo de caja negativo generado por los costos y gastos fijos. Entonces, para determinar si es conveniente cerrar temporalmente, se compara el flujo de caja generado por la operación con el flujo de caja generado por los costos fijos, si el primero es mayor (es decir, menos negativo). Por lo tanto, aun siendo negativo se continuaría con la operación; mientras que si el flujo de caja generado fuera menor (más negativo) que el flujo del costo fijo, se optaría por cerrar temporalmente la mina hasta que los precios se recuperen.
El flujo de caja del período, ya sea porque se opera o porque la mina está cerrada y se “soportan” los costos fijos, estaría dado por la siguiente expresión:
FC=MAX (FCL, FC costos fijos)
Si FCL>FC costos fijos, entonces la operación continúa; mientras que si FCL<FC costos fijos entonces la mina se cierra temporalmente.
En ambos casos se han realizado 10 000 simulaciones para calcular el VA. La diferencia entre el VA con opción menos el VA sin opción será el valor de la opción.
Valor de la opción=VA con opción de cierre – VA sin opción de cierre
5.3Resultados obtenidosEn las proyecciones de flujos de caja realizadas, tanto para el escenario alcista como para el bajista se ha considerado la tasa libre de riesgo que se aproxima a 4.8%, que es la tasa de rendimiento de los bonos soberanos peruanos9 emitidos en PEN, para un plazo de 18 años.
Después de realizar 10 000 simulaciones, los resultados obtenidos para el escenario alcista, se pueden ver en la tabla 1.
El valor de la opción sería de 151 510 millones de dólares, que es la diferencia entre ambos valores. Mientras que en un escenario bajista (véase la tabla 2), el valor de la opción, para este caso, sería de 158 112 millones de dólares.
Se puede apreciar, en ambos casos, que la opción de cierre temporal mejora los resultados, ya que se obtiene un mayor VA. También se observa que el valor de la opción en el caso bajista es mucho mayor que para el caso alcista, lo cual resulta razonable, dado que en el caso de que los precios bajen demasiado será preferible frenar las operaciones, e iniciarlas nuevamente cuando las condiciones cambien; aunque se tendría que afrontar tanto los costos de mantenimiento como el impacto social y económico que ocasionaría en la comunidad.
6ConclusionesEste documento analiza específicamente un modelo estocástico unifactorial de precios de commodities aplicado al caso del oro. El modelo presentado tiene la ventaja de permitir extender sin dificultad la mayoría de los modelos de precios de commodities que han sido propuestos en la literatura. Se realizó, además, un análisis de identificación de los parámetros, que posibilitó desarrollar una representación canónica del modelo de precios. Esta representación contiene el mínimo número de parámetros y permite obtener soluciones únicas, lo que contrasta con la mayoría de los modelos de precios planteados en la literatura, en los que se llega, algunas veces, a fórmulas de valorización bastante complejas.
Las estimaciones empíricas realizadas a partir de observaciones mensuales de precios spot del oro, dieron la posibilidad de analizar el comportamiento del modelo propuesto. El análisis fue realizado considerando la estructura de la volatilidad empírica. El procedimiento de estimación de los parámetros del modelo no es sofisticado; se basa en regresiones por mínimos cuadrados utilizando las series históricas de precios logrando, sin embargo, ser coherente con el nivel de aplicación postulado.
La velocidad de reversión a la media encontrada no es tan veloz como lo es para otros commodities, como por ejemplo el cobre o el petróleo; no obstante, la velocidad encontrada coincide con lo esperado.
Evaluar proyectos mediante el enfoque de opciones reales permite valorizar en su real magnitud los beneficios económicos asociados a un proyecto de inversión, debido a que se tiene en cuenta el trinomio rentabilidad-riesgo-flexibilidad, integrando la perspectiva estratégica y el análisis financiero de valoración de proyectos.
Las condiciones de incertidumbre de los mercados —a nivel mundial— obligan a los tomadores de decisión a utilizar nuevas formas de evaluación de sus inversiones. En este sentido, la metodología desarrollada contribuye a demostrar el efecto y el impacto que puede tener en las decisiones estratégicas la correcta cuantificación de las variables inciertas de los mercados de commodities.
Bajo supuestos válidos, a la empresa le resulta beneficioso detener sus operaciones cuando el precio caiga, y retomar las operaciones cuando los precios suban nuevamente. Aunque se debe tener en cuenta que no se han considerado los costos de cierre, mantenimiento y apertura, así como los costos sociales que implicaría suspender la actividad minera.
De acuerdo con los resultados encontrados, es posible afirmar que la valorización a través de opciones reales añade valor a la empresa, pues se demuestra que la incertidumbre juega un rol importante en las oportunidades de inversión. Por el contrario, si hubiéramos encontrado un mayor nivel de reversión a la media, menor habría sido el valor de la oportunidad de inversión. Además de valorizar un proyecto de inversión, el análisis de opciones reales puede determinar, también, la política óptima que maximiza el valor del proyecto.
Valerse de opciones reales implementa un procedimiento numérico conocido, que va de la mano del modelo de precios elegido; por lo tanto, se dejan de lado variables que pueden resultar relevantes en una evaluación de inversiones más rigurosa.
La aplicación de los conceptos de finanzas modernas en mercados de commodities puede manifestarse muchas veces compleja y muy sofisticada; sin embargo, la metodología presentada logra ser simple, encontrándose resultados interesantes y coherentes que sirven de apoyo en la toma de decisiones de inversión en proyectos mineros. Para este caso, la simulación por Montecarlo parece ser el mejor método para valorar, ya que la opción puede ser ejercida en varios períodos de tiempo.
El presente estudio ha intentado la convergencia de conceptos de finanzas modernas con mercados de commodities; por lo tanto, los trabajos futuros propuestos podrían seguir esta línea de investigación. Por ejemplo, mejorando la modulación de los precios a través de un modelo desarrollado particularmente para las características dinámicas del mercado del oro, integrando conceptos de análisis econométrico y de procesos estocásticos de mayor sofisticación. En este sentido, modelar la estructura de volatilidad con un proceso no estacionario, incluyendo los saltos que afectan los precios y los efectos periódicos, mejorando eventualmente el procedimiento de estimación.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Doctor en Economía y Dirección y Administración de Empresas.
Economista.
Modelos que se derivan de los modelos de precios de commodities desarrollados en las finanzas modernas.
El proceso estocástico, llamado movimiento browniano o proceso de Wiener, es un modelo utilizado en diversas ramas de la ciencia y de singular importancia para las finanzas. Prácticamente todos los modelos a tiempo continuo que se utilizan en las finanzas modernas se basan es este proceso; esto se debe a que a partir de él se construyen modelos de precios de activos financieros y de tasas de interés. El movimiento browniano cumple con que sus trayectorias en ningún punto tienen derivada; es decir, está formado únicamente por picos y es por eso que no se puede hablar sobre la velocidad de una trayectoria posible del movimiento browniano.
Para realizar la regresión se ha trabajado con el logaritmo natural del precio y no con el precio en sí mismo, a fin de evitar problemas de raíces unitarias, ya que si las tuviéramos no habría proceso de reversión, y también para eludir heterocedasticidad. Cabe mencionar que no existen problemas de autocorrelación con la regresión realizada, teniendo en cuenta lo primero.
Analista y asesor financiero especializado en metales preciosos y materias primas. B. Schmidt se ha dedicado a analizar el mercado de metales preciosos, materias primas y energía, desde el año 2000. Fue analista y consultor para uno de los fondos de oro y materias primas más influyentes de Alemania. Con más de 12 años de experiencia en el sector financiero, B. Schmidt es analista y asesor autónomo desde 2004.
Medida central de la fortaleza financiera de un banco desde el punto de vista del regulador. Se compone de un capital básico, que consiste principalmente en las acciones ordinarias y las reservas declaradas (o utilidades retenidas), pero también puede incluir las acciones preferenciales no acumulativas no redimibles.
Calculado a través de H=ln2/k.
El informe argumenta que la cotización del oro se ha resentido como consecuencia de la crisis crediticia en la zona del euro, de un dólar más fuerte y de la consecuente debilidad de la moneda europea. La crisis crediticia se encontraría lastrando el crecimiento mundial y fortaleciendo al dólar, lo que estaría frenando la demanda industrial y de inversión de estos metales. Pero los expertos de Morgan Stanley puntualizan que las razones para un rally alcista en la cotización del oro continúan intactas, y que el metal dorado se beneficiaría de las tasas de interés negativas en Estados Unidos, los problemas sin solventar de la Zona Euro y de las posibles medidas de estímulo económico de los bancos centrales.
Se ha tomado esta empresa como referencia debido a que realiza sus labores de explotación por socavón y a que cotiza en la Bolsa de Valores de Lima, haciendo que su información financiera publicada sea fiable.
Se utilizaron los bonos soberanos peruanos teniendo en cuenta la opinión de la economista del Departamento de Investigación para América Latina del Credit Suisse, Carola Sandy, quien recomienda el posicionamiento sobre dichos bonos: «Estamos a favor de los bonos soberanos de corto plazo (en soles), donde los rendimientos están bien anclados por la estabilidad de la moneda y la política monetaria que ejerce el Banco Central de Reserva (BCR)».