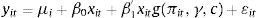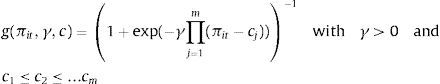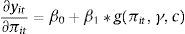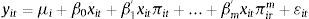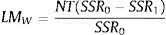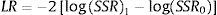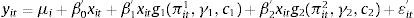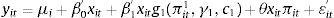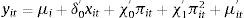The relationship between inflation and economic growth is a contentious issue. The present study is undertaking to test hypothesis that the relationship between inflation and economic growth is nonlinear. This pane data study involves ASEAN-5 countries over the period 1980–2011. Panel Smooth Transition Regression (PSTR) model is employed to estimate the threshold of inflation and its effects on economic growth. Furthermore, we also check robustness by using GMM-IV specification. The study finds that there exists a statistically significant negative relationship between inflation and growth for the inflation rates above the threshold level of 7.84%, above which inflation starts impeding economic growth in the ASEAN-5 countries. The results suggest that central banks in the ASEAN-5 countries could improve economic growth by reducing inflation when it is above or near the estimated thresholds. The threshold inflation level can be considered, therefore, as inflation targeting indicator to conduct monetary policy.
La relación entre la inflación y el crecimiento económico es una cuestión polémica. El presente estudio trata de probar la hipótesis de no linealidad la relación entre la inflación y el crecimiento económico. Este estudio de regresión fluida incluye a los países ASEAN-5 durante el periodo 1980–2011. Se utiliza el modelo -Panel Smooth Transition Regression (PSTR)- para calcular el umbral de la inflación y sus efectos sobre el crecimiento económico. Además, revisamos también la solidez utilizando la especificación GMM-IV. El estudio encuentra que existe una relación negativa estadísticamente significativa entre la inflación y el crecimiento para las tasas de inflación superiores al umbral del 7.84%, por encima del cual la inflación impide el crecimiento económico en los países del sudeste asiático. Los resultados sugieren que los bancos centrales de estos países podrían mejorar el crecimiento económico mediante la reducción de la inflación, cuando esta es superior o cercana a los umbrales estimados. Por tanto, el nivel umbral de la inflación puede considerarse como un indicador objetivo de la misma para la realización de las políticas monetarias.
Inflation's effects on an economy are various and can be simultaneously positive and negative. The relationship between inflation and economic growth is the subject that has long been intensely discussed and debated in the literature (López-Villavicencio & Mignon, 2011). A high economic growth in relation with low and stable inflation is the main objective of macroeconomic policy (Khan & Senhadji, 2001; Seleteng, Bittencourt, & van Eyden, 2013; Vinayagathasan, 2013). Some studies provide evidence that inflation has negative impact on medium and long run growth (Khan & Senhadji, 2001). These findings imply that inflation maintained at a certain magnitude is necessary to foster the development of economy. All schools of economic thought have not favored accelerating inflation for undesirable distribution and social welfare effects (Eggoh & Khan, 2014). In the literature, various factors are considered as strong forces for determining and controlling price inflation. These factors include money supply, interest rate, potential output, exchanges rate, wage rate, trade openness and expectations (Zaman, Khan, Ahmad, & Ikram, 2011; Naz, Mohsin, & Zaman, 2012; Bhattacharya, 2014; Ghosh, 2014).
If inflation is detrimental to economic growth, the policy makers may keep low rates of inflation in order to achieve economic policy targets. Inflation targeting is a helpful policy tool in controlling inflation (Ayres, Belasen, & Kutan, 2014; Öztürk, Sözdemir, & Ülger, 2014). However, a few questions remain unanswered that how low is inflation rate? At what level is inflation detrimental to long-term economic growth? Answering these questions, it is not surprising that optimal level of inflation is detected in several recent empirical studies (see Ghosh & Phillips, 1988; Sarel, 1996; Khan & Senhadji, 2001; Bick, 2010; Seleteng et al., 2013; Vinayagathasan, 2013; Baglan & Yoldas, 2014; Eggoh & Khan, 2014). Optimal level or threshold level of inflation is at inflexion point which positive effects of inflation on growth exist when the inflation rate is low and negative effects when the inflation rate is high (Seleteng et al., 2013). If threshold level of inflation exists, the relationship between inflation and growth is non-linear, switching from positive to negative. Although, it seems that non-linear relationship of inflation and growth is widely accepted, there are still controversies about (i) the threshold level of inflation; (ii) the change of this relationship to used methodology, studied countries and time series... The threshold level is various depending upon country-specific characteristics (Khan & Senhadji, 2001; Eggoh & Khan, 2014; and Baglan & Yoldas, 2014). These authors explain that country-specific and time-specific structural break in inflation-growth relationship is higher for developing economies than for developed ones.
The recent years have seen an increase in the degree of social and economic integration in the members of ASEAN. The ASEAN Economic Community will be the goal of regional economic integration by 2015. They are emerging economies, while their initial development conditions are various. ASEAN countries show wide diversity in level of economic development, income per capita and inflation. Means of inflation rates in ASEAN countries ranged from 3.13 to 62% over the period of 1980-2011. The lowest inflation rates were observed in Malaysia and Thailand, at 3.13 and 4.35%, respectively, while the highest was posted by Vietnam, at 62%. Indonesia and Philippines maintained inflation rates at 9.18 to 10.5%, respectively. Meantime, the ASEAN countries showed rather low real GDP growth rate per capita. The lowest growth rate was posted by Philippines, at close to 1%, whereas the highest rate was topped by Vietnam at 4.6%. Malaysia, Indonesia and Thailand managed to temper growth rate from 3.3 to 3.7 and 4.02%, respectively (see Table 1). Table 1 also shows preliminary relationships between inflation and growth in the ASEAN countries. Countries such as Thailand and Malaysia had moderate growth rate when accompanied by a low inflation rate in long run. High level of inflation halted economic growth for Philippines in long run.
Mean of real GDP growth rate per capita and mean of inflation rate over the period of 1980-2011 in the ASEAN-5 countries.
| Country | Real GDP growth rate per capita (%) | CPI % |
|---|---|---|
| Indonesia | 3.73 | 10.53 |
| Malaysia | 3.33 | 3.13 |
| Philippines | 0.85 | 9.18 |
| Thailand | 4.02 | 4.35 |
| Vietnam | 4.62 | 62.06 |
Author's calculation using data from Penn World Table (8.0) and Economy Watch.
In the ASEAN's region context, research in inflation-growth non-linear relationship has been rather few. We hypothesize that there exists non-linear relationship between inflation and growth in the ASEAN countries. The present study is designed to test the hypothesis by empirically estimating threshold level of inflation and the smoothness of the transition from a low to high regime inflation in the ASEAN-5 countries, namely Indonesia, Malaysia, the Philippines, Thailand and Vietnam. By using a panel data of the ASEAN-5 countries over the period of 1980-2011, we adopt the Panel Smooth Transition Regression (PSTR) model developed by González, Teräsvirta and Dijk (2005) and GMM-IV specification for inflation threshold and inference. With regard to the specifications of panel analysis or PTR, the main advantage of the PSTR is that it allows the inflation-growth coefficient to vary according to the country and with the time. The PSTR model allows individuals move between groups and over time depending on changes in the threshold variable. The PSTR model also provides a parametric approach of the cross-country heterogeneity and of the time instability of the inflation-growth coefficients, since these parameters change smoothly as a function of a threshold variable.
The remainder of the paper is as follows. The next section briefly presents previous literature review. Section 3 reviews panel threshold estimation. Section 4 introduces variables and data. Section 5 presents the estimated results for the inflation-growth nexus. Finally, Section 6 concludes the study.
2Literature reviewWhat level of inflation is harmful to economic growth? Economic theories come to various conclusions about the response of output growth to inflation. The aggregate supply-aggregate demand (AD-AS) model also explains a positive relationship between inflation and output growth where, as output rises, so do inflation. Phillips curve shows a trade-off between inflation and unemployment rate. Phillips curve interprets that the higher rate of inflation, the lower the unemployment and vice-versa. However, Phillips curve fails to justify the situations of stagflation, when both inflation and unemployment are alarmingly high. Keynesian and Neo-Keynesian theory provide a more comprehensive model for linking inflation to growth under the AD-AS framework. Under this model, there is a short-run trade-off between output and the change in inflation, but no permanent trade-off between output and inflation. The quantity theory of money emphasizes the critical role of monetary growth in determining inflation. Monetarism suggests that if the growth in the money supply is higher than the output growth, inflation will result. Neo-classical and endogenous growth theories account for the effects of inflation on growth through its impact on investment and capital accumulation. In general, each economic theory makes its particular contribution to the inflation-growth relationship. No schools of economic thought have favored accelerating inflation for undesirable distribution and social welfare effects. Inflation's effects on growth are subject to certain macroeconomic conditions that can vary substantially from one country to another (Eggoh & Khan, 2014). Thus, in empirical studies various factors are considered as strong forces for determining and controlling price inflation. These factors include money supply, interest rate, potential output, exchanges rate, wage rate, trade openness and expectations (Zaman et al., 2011; Naz et al., 2012; Bhattacharya, 2014; Ghosh, 2014).
While doubts that very high inflation is bad for growth, empirical studies conducted in the last two decades have clearly confirmed the negative and nonlinear impact of inflation on economic growth. In empirical models, inflation-growth nexus is employed within an optimal economic growth framework incorporating several exogenous variables. A study by Gylason and Herbertsson (2001) reports the existence of a non-linear relationship between inflation and growth for 170 countries over the period of 1960–1992. The paper finds that inflation in excess of 10-20% per year is generally detrimental to economic growth. In addition, using a panel of 140 countries comprising of developed and developing countries for the period of 1960-1998, Khan and Senhadji (2001) use threshold estimation technique of Hansen (2000) and find that threshold inflation levels exit at 1-3% for developed countries; 7-11% for developing countries and 8-12% for all countries, respectively. Inflation rates above the threshold level have negative and negative effects on growth. Results depict non-linear relationship of inflation and growth. Similarly, based on a generalization of Hansen (1999) panel threshold model by allowing for regime intercepts, Bick (2010) reexamines the relationship between inflation and economic growth for 40 countries through the period of 1960-2004. The study finds that in absence of regime intercepts, threshold level of inflation is 19% and inclusion of a regime intercept decreases the threshold from 19% to 12%.
Above studies have exogenously determined the threshold and tested for empirical significance. Recent authors use PSTR model to resolve the drawback of the external threshold determination. Omay and Öznur Kan (2010) analyze empirical relationship between inflation and growth using PSTR model for six industrial countries in the period of 1972-2005. They provide evidence that there exists the inflation threshold level of 2.52%. Relationship between inflation and growth is negative when inflation rates are above this threshold level. After testing the robustness of this relationship by using Seemingly Unrelated Regression (SUR), the threshold levels change slightly from 2.42% to 3.18%, respectively. A similar study is carried by López-Villavicencio and Mignon (2011), who estimate the growth effects of inflation on a sample of 44 countries in the period of 1961-2007. Based on PSTR and GMM models, they find that inflation non-linear impacts the growth with threshold level of 5% for whole sample, 1.23% for developed countries, 14.54% for emerging countries, 10.273% for upper middle countries and 19.64% for lower middle and low countries, respectively. They conclude that above the threshold, which inflation has a negative effect on growth and below which it enhances growth for developed countries. In addition, Seleteng et al. (2013) use PSTR model to estimate the inflation and-growth relationship in the South African Development Community (SADC) region over the period of 1980–2008. The study finds a threshold level of 18.9% in the SADC region. Eggoh and Khan (2014) examine the threshold effects in the inflation-growth relationship by a panel of 102 developed and developing countries over the period of 1960-2009 applying PSTR and GMM models. They also control some country-based macroeconomic characteristics such as financial development, capital accumulation, trade openness and government expenditures, which influence this relationship. The results specially show that a threshold level of 10.5% for global, 3.4% for high-income countries, 10% for upper middle-income countries, 12.9% for lower middle-income countries and 19.5% for lower income countries, respectively. Using data with a balanced panel of 92 developing countries from 1975 to 2004, Baglan and Yoldas (2014) estimate a flexible semi-parametric panel data model and find that inflation becomes a significant detriment to growth only after it reaches about 12%. Moreover, they also find that the relationship ceases to be statistically significant at very high levels of inflation.
From above empirical studies, there seem to be consensus that existence of inflation-growth relationship is non-linear. The empirical studies of this relationship are, however, inconclusive and the results are various with respect to model specifications and data. Threshold inflation levels for developing countries are around 12%-19%, which are higher as compared to developed countries.
Jiranyakul and Opiela (2010) argue that ASEAN countries have low inflation relative to other emerging markets. Indeed, in the ASEAN's region context, research in inflation-growth non-linear relationship has been rather few. To my best knowledge, there is a study for Malaysia. Munir, Mansur and Furuoka (2009) examine the relationship between inflation rate and growth in the context of Malaysia, using endogenous threshold autoregressive (TAR) model proposed by Hansen (1999; 2000) for estimation and inference. The paper uses annual data from Malaysia for the period 1970-2005. The estimated results suggest 3.89% as the threshold level of inflation above which inflation significantly hurts growth and below the threshold level, there is a statistically significant positive relationship between inflation rate and growth. This implies a non-linear relationship between inflation and growth for Malaysia. There is another study for Asian, including developed and developing countries. Vinayagathasan (2013) investigates the threshold level of inflation for 32 Asian countries over the period of 1980–2009 by employing a dynamic panel threshold model allowing for fixed effects and endogeneity. The finding reveals that an inflation threshold of approximately 5.43% and above which inflation is detrimental to growth but has no effects below this level. After extracting the data of four OECD (Japan, Korea, Israel and Turkey) and Singapore, the study also confirms that the effects of inflation on growth are also the same as for the full sample. From these results, we find that threshold levels for developing countries in Asia region may be lower than those for other developing countries as found by Bick (2010), López-Villavicencio and Mignon (2011), and Baglan and Yoldas (2014).
Our study explores the relation between inflation and growth for the ASEAN-5 countries. We employ a PSTR model to estimate. The countries we choose are emerging markets in ASEAN region, including namely Indonesia, Malaysia, the Philippines, Thailand and Vietnam. The ASEAN-5 countries have both low to moderate average inflation over our sample. The ASEAN-5 countries have also a wider variance in their average inflation rates. These differences in initial output conditional characteristics may have an impact on the relation between inflation and growth. Hence, it may be of interest to explore this relation for these economies.
3Methodology3.1PSTR modelTo detect the potential non-linear relationship between inflation and growth, we use PSTR model developed by González et al. (2005). We express the simplest case of a PSTR with threshold one or two extreme regimes and a single transition function to illustrate relationship between inflation (πit) and growth (yit):
Where i = 1….N, t = 1…..T; N and T denote the cross-section and time dimensions of the panel, respectively; μi represents the fixed individual effect and εit is the errors. The dependent variable yit is a scalar, xit is a k-dimensional vector of time-varying control variables. Transition function g(πit,γ,c) is a continuous function and depends on threshold variable (πit) and normalized to be bounded between 0 and 1, and these extreme values are associated with regression coefficients β0 and (β0+β1). González et al. (2005) consider, following Granger and Teräsvirta (1993) for the time series STAR models, the following logistic transition function:Where cj=(c1,....,cm)', which is an m – dimensional vector of parameters; the slope parameter γ determines the smoothness of the transition. For m = 1, the model has the two extreme regimes separating low and high values of πit with a single monotonic transition of the coefficients from β0 to (β0+β1) as πit increases. For a higher value γ, the transition becomes rougher and transition function g(πit,γ,c) becomes the indicator function g(πit,c). When γ tends towards infinite, indicator function g(πit,c) =1 if event πit>c occurs, and indicator function g(πit,c) = 0 otherwise. When γ is close to 0, the transition function g(πit,γ,c) is constant. In that case, the PSTR converges towards the two–regime panel threshold regression (PTR) of Hansen (1999). In general, for any value of m, the transition function g(πit,γ,c) is constant when γ is close to 0. In which case, the model in Eq. (1) becomes a linear panel regression model with fixed effects.With regard to the specifications of panel analysis or PTR, the main advantage of the PSTR is that it allows the inflation-growth coefficient to vary according to the country and with the time. The PSTR model allows individuals move between groups and over time depending on changes in the threshold variable. The PSTR model also provides a parametric approach of the cross-country heterogeneity and of the time instability of the inflation-growth coefficients, since these parameters change smoothly as a function of a threshold variable. The elasticity of growth to inflation for the ith country at the time t is defined as follows:
3.2Model specification testsGonzález et al. (2005) propose the following specification procedure for PSTR: (i) Test the linearity against the PSTR model; (ii) Parameter estimation; (iii) Test for number of transition function.
(i) Testing for linearity
Testing the linearity in a PSTR model, Eq. (1) can be done by testing H0:γ=0 or H0: β0=β1. However, in both cases, the test will be nonstandard since under H0 the PSTR model contains unidentified nuisance parameters. This issue is evident from the literature devoted to the time series threshold models (Hansen, 1999). Therefore, González et al. (2005), following Luukkonen, Teräsvirta and Dijk (1998) replace g(πit,γ,c) in Eq. (1) by its first–order Taylor expansion round γ=0 and obtain the auxiliary regression:
Where the parameter vectors (β1',.....,βm') are multiples of γ and εit'=εit+Rmβ1'xit, where Rm is the remainder of Taylor expansion. Thus, testing H0 in Eq. (1) is equivalent to testing the H0*:β1'+....+βm'=0 in Eq. (4). This null hypothesis may be conveniently tested by a Wald and Likelihood ratio tests. If we denote SSR0 the panel sum of squared residuals under H0 (linear panel model with individual effects) and SSR1 the panel sum of squared residuals under H1 (PSTR model with two regimes), the Wald LM test can be written as:The Likelihood ratio test can be written as:
(ii) Parameter estimation
The parameters (β0',β1',γ,c) in Eq. (1) are estimated in 2 steps: (i) eliminate the individual effects by removing individual-specific means and (ii) apply nonlinear least squares (NLS) to the transformed data.
We apply NLS to determine the values of these parameters that minimize the concentrated sum of squared errors. While estimating the PSTR model, a practical issue that deserves special attention is the selection of starting values for γ and c such that γ>0, ci,min>min(πit), cj,max (iii) Testing for the number of transition function The logic is similar when it comes to testing the number of transition functions (r) in the model or equivalently order of extreme regimes (r+1). (González et al., 2005) propose a sequential approach by testing the null hypothesis of no remaining nonlinearity in the transition function. In the PSTR framework, we assume that the linearity hypothesis is rejected. The issue is then to test whether there is one transition function (H0:r=1) or whether there are at least two transition functions (H0:r=2). Consider the model with r=2 or three regimes:
We can replace the second transition function (πit2,γ2,c2) by its first-order Taylor expansion around γ2=0, and then in testing linear constraints on the parameters. Therefore, the model in Eq. (7) becomes:
The test of no remaining nonlinearity is simply defined by H0:θ=0. Let us denote SSR0 the panel sum of squared residuals under H0, i.e. in a PSTR model with one transition function. Let us denote SSR1 the sum of squared residuals of the transformed model in Eq. (8). The testing procedure is then as follows. Given a PSTR model with r=r*, we will test the null H0:r=r* against H1:r=r*+1. If H0 is not rejected the procedure ends. Otherwise, the null hypothesis H0:r=r*+1 is tested against H0:r=r*+2. The testing procedure continues until the first acceptance of H0.
3.3Robust testFor the robustness tests, we employ a growth regression, which contains a quadratic interaction term as follows:
The interaction term is included in Eq. (9) to investigate nonlinear growth effects of the threshold variable. This allows us to detect whether, beyond a certain level, the threshold variable becomes more or less important in determining the marginal effect of inflation on growth.
In estimating Eq. (9), differenced generalized method-of-moments (GMM) or system GMM are not used because consistency of results using these methodologies depends crucially on having a large number of cross-sectional units, regardless of the number of time series observations. However, our sample by contrast has only five cross-sectional observations and a relatively large number of periods. We instead estimate the model using GMM-IV (General Method of Moments with instrumental variables). GMM-IV estimator is implemented in the standard IV and 2SLS estimator. This methodology gives us coefficient estimates that are corrected for endogeneity, heteroskedasticity and autocorrelation. Lagged values of the endogenous variables are used as instruments.
GMM-IV estimation provides a straightforward way to test the specification of the proposed model through the Hansen J test. A simple application of Hansen J test statistic is to test the validity of over identifying restrictions, under the null hypothesis that the over identifying restrictions are satisfied. Pagan and Hall test for heteroskedasticity is used in GMM-IV model. The idea behind the test —similar to that of the Breuch-Pagan and White tests for heteroskedasticity— is that if any of the exogenuos variables can predict the squared residual, the errors are conditionally heteroskedastic. Under the null of conditional heteroskedasticity in GMM-IV regression, the Pagan-Hall statistic is distributed as χp2, irrespective of presence of heteroskedasticity elsewhere in the system. All of these characteristics of this modeling technique yield results comparable to those of the PSTR model.
4Variables and dataThis article employs the panel data, consisting of the ASEAN-5 countries (Indonesia, Malaysia, the Philippines, Thailand and Vietnam) and the period of 1980-2011. We collect the dataset from Penn World Table (PWT) 8.0 and the Economy Watch (EW). To estimate the relationship between inflation (πit) and growth (yit), we choose a set of the most important control variables (xit) among the large set found in empirical growth literature such as Barro (1991), Sala-i-Martin (1997), Khan and Senhadji (2001), López-Villavicencio and Mignon (2011), Vinayagathasan (2013), Baglan and Yoldas (2014), Eggoh and Khan (2014).
- •
The initial level in growth (y0it) used to control for productive capacity in the spirit of the neoclassical growth theory.
- •
Some determinants in endogenous growth theory that are proxy for macroeconomic policies, institutions and trade are included such as employment growth rate (popit), investment growth rate (invit), government spending growth rate (govit), growth rate of terms of trade (totit) and standard deviation of terms of trade (sdtotit).
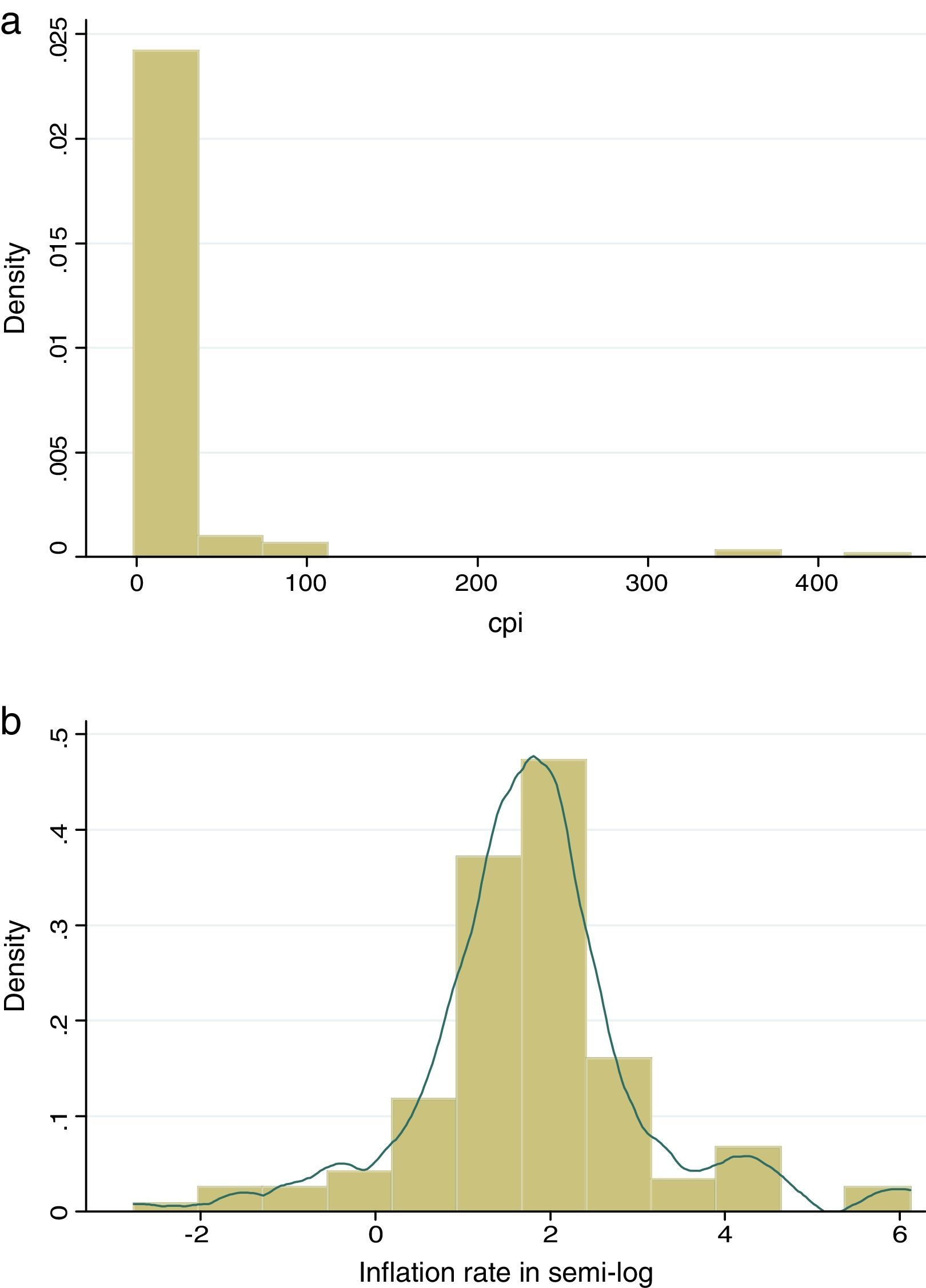
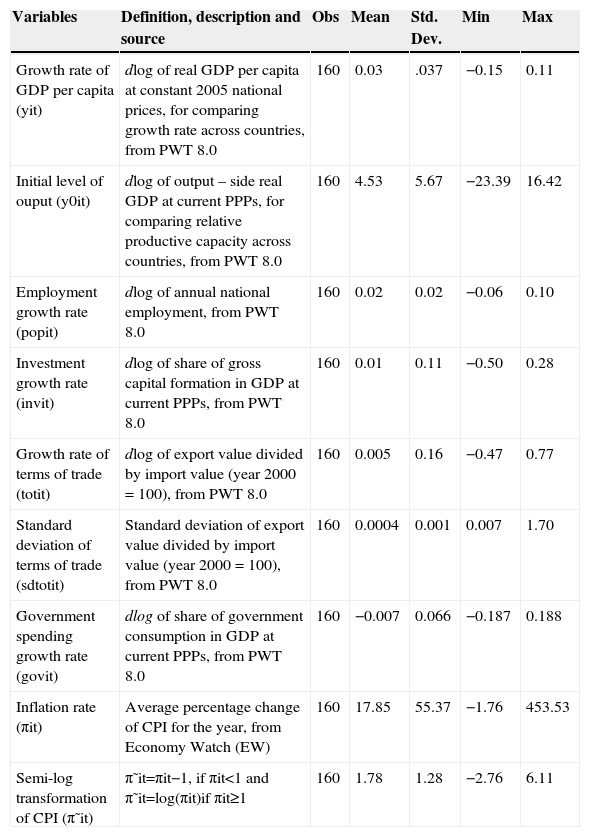
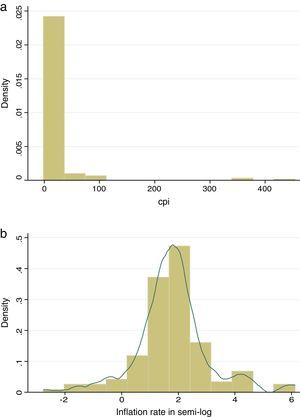
Table 2 explains definitions and descriptive statistics of variables in our growth regression. The growth rate of a variable x is computed as the first difference of log(x), dlog(x). Our main variable of interest is inflation rate (πit). The average inflation rate of the ASEAN-5 countries is 17.8%. Some negative inflation observations exist in our sample. Therefore, we use a semi-log transformation of inflation with π˜it=πit−1, if πit<1 and π˜it=log(πit), if πit≥1. The log transformation reduces the asymmetry in the initial distribution of inflation and provides the best fit among nonlinear models. Figure 1a shows asymmetric distribution of inflation rate. Figure 1b reveals the symmetric distributions of inflation in semi-log with normal distribution for the ASEAN-5 countries over the period of 1980-2011. Standard deviation of inflation rate in semi-log is very small; it is only 1.78%.
Definitions and descriptive statistics of variables.
| Variables | Definition, description and source | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| Growth rate of GDP per capita (yit) | dlog of real GDP per capita at constant 2005 national prices, for comparing growth rate across countries, from PWT 8.0 | 160 | 0.03 | .037 | −0.15 | 0.11 |
| Initial level of ouput (y0it) | dlog of output – side real GDP at current PPPs, for comparing relative productive capacity across countries, from PWT 8.0 | 160 | 4.53 | 5.67 | −23.39 | 16.42 |
| Employment growth rate (popit) | dlog of annual national employment, from PWT 8.0 | 160 | 0.02 | 0.02 | −0.06 | 0.10 |
| Investment growth rate (invit) | dlog of share of gross capital formation in GDP at current PPPs, from PWT 8.0 | 160 | 0.01 | 0.11 | −0.50 | 0.28 |
| Growth rate of terms of trade (totit) | dlog of export value divided by import value (year 2000 = 100), from PWT 8.0 | 160 | 0.005 | 0.16 | −0.47 | 0.77 |
| Standard deviation of terms of trade (sdtotit) | Standard deviation of export value divided by import value (year 2000 = 100), from PWT 8.0 | 160 | 0.0004 | 0.001 | 0.007 | 1.70 |
| Government spending growth rate (govit) | dlog of share of government consumption in GDP at current PPPs, from PWT 8.0 | 160 | −0.007 | 0.066 | −0.187 | 0.188 |
| Inflation rate (πit) | Average percentage change of CPI for the year, from Economy Watch (EW) | 160 | 17.85 | 55.37 | −1.76 | 453.53 |
| Semi-log transformation of CPI (π˜it) | π˜it=πit−1, if πit<1 and π˜it=log(πit)if πit≥1 | 160 | 1.78 | 1.28 | −2.76 | 6.11 |
Source: Penn World Table (PWT) 8.0 and the Economy Watch (EW).
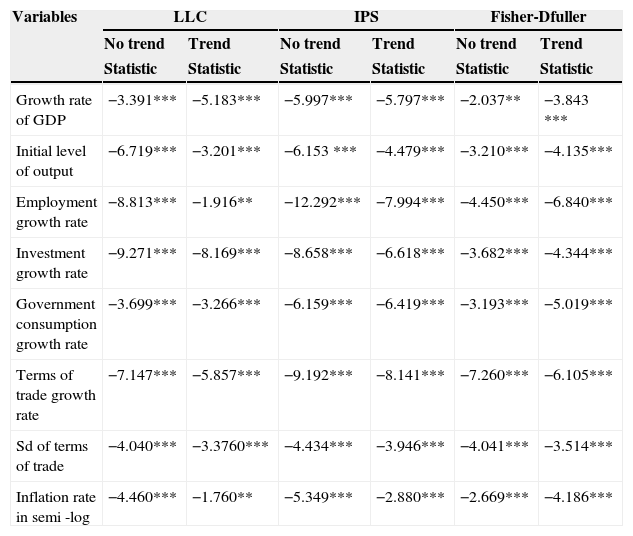
All the asymptotic theory for STR models and also PSTR model extended by González et al. (2005) are for stationary regressors. Therefore, the procedures of PSTR specification rely on the assumption that all variables in Eq. 1 are I(0) process. In order analyze stationarity properties of the data, we test whether the data have a unit root by panel unit root tests. Table 3 shows that stationarity results are estimated by test statistics of Levin–Lin–Chu (LLC) (Levin, Lin, & Chu, 2002), Im–Pesaran–Shin (IPS) (Im, Pesaran, & Shin, 2003) and Fisher-Dfuller (Choi, 2001) with trend and no trend. The LLC, IPS and Fisher-Dfuller tests reject the null hypothesis at 1% and 5% significance level in the examined series. From these results, we can conclude that all variables in the study are I(0) process.
Unit root test statistics.
| Variables | LLC | IPS | Fisher-Dfuller | |||
|---|---|---|---|---|---|---|
| No trend | Trend | No trend | Trend | No trend | Trend | |
| Statistic | Statistic | Statistic | Statistic | Statistic | Statistic | |
| Growth rate of GDP | −3.391*** | −5.183*** | −5.997*** | −5.797*** | −2.037** | −3.843 *** |
| Initial level of output | −6.719*** | −3.201*** | −6.153 *** | −4.479*** | −3.210*** | −4.135*** |
| Employment growth rate | −8.813*** | −1.916** | −12.292*** | −7.994*** | −4.450*** | −6.840*** |
| Investment growth rate | −9.271*** | −8.169*** | −8.658*** | −6.618*** | −3.682*** | −4.344*** |
| Government consumption growth rate | −3.699*** | −3.266*** | −6.159*** | −6.419*** | −3.193*** | −5.019*** |
| Terms of trade growth rate | −7.147*** | −5.857*** | −9.192*** | −8.141*** | −7.260*** | −6.105*** |
| Sd of terms of trade | −4.040*** | −3.3760*** | −4.434*** | −3.946*** | −4.041*** | −3.514*** |
| Inflation rate in semi -log | −4.460*** | −1.760** | −5.349*** | −2.880*** | −2.669*** | −4.186*** |
Note: (***), (**) denote significance at 1% and 5%, respectively.
Author's estimation using STATA 13.
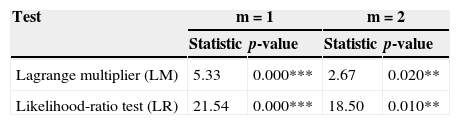
For the test of linearity, we check whether the order m is one or not. The results of the specification test in Eq. (1) are presented in Table 4. The table shows the p-value of Lagrange multiplier and Likelihood-ratio test for the null hypothesis of linearity against the alternative of logistic (m=1) or exponent (m=2) PSTR specification. We find that the null hypothesis of linearity is rejected at the 1% significance level. Moreover, rejection of linearity is stronger for m=1, the logistic specification (m=1) is preferred to exponent one (m=2). The results imply that there exists non-linear relationship between inflation and growth in the ASEAN-5 countries. We thus employ the estimation of non-linear growth model by using the PSTR estimation and GMM-IV specification.
LM and LR test of linearity.
| Test | m=1 | m=2 | ||
|---|---|---|---|---|
| Statistic | p-value | Statistic | p-value | |
| Lagrange multiplier (LM) | 5.33 | 0.000*** | 2.67 | 0.020** |
| Likelihood-ratio test (LR) | 21.54 | 0.000*** | 18.50 | 0.010** |
Note: (***), (**) denote significance at 1% and 5%, respectively.
H0: Linear model; H1: PSTR model with m=1 or m=2.
Author's estimation using STATA 13.
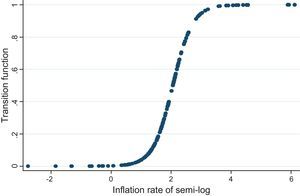
In the next step, we start a grid search to obtain threshold values c for the PSTR model. The optimal threshold value is one that minimizes the sequence of RSS in Eq (1). Table 5 presents the test results for the existence of threshold value and provides information about transition parameter γ. We conduct the search from 1% to 90% for the sample, which yields 90 panel regressions of equation (1). The minimization values of the RSS, AIC and BIC are reached at the semi-log π˜it = 2.059, which is converted to 7.84% (πit). The results suggest that the estimated threshold value c is 7.84% and the transition parameter γ is 3.04.
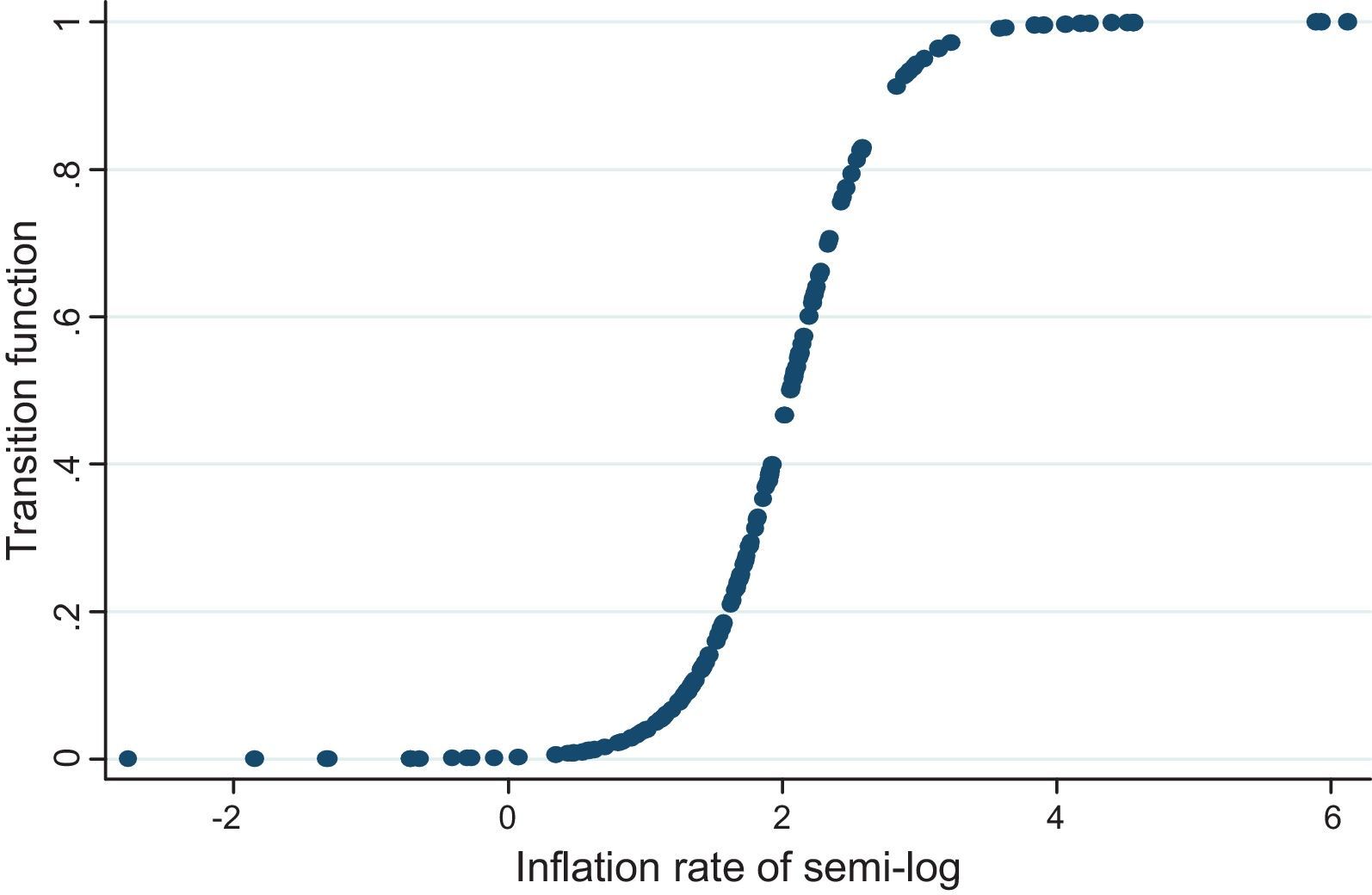
Figure 2 shows the transition function with respect to the transition variable (π˜it), threshold value c = 2.059 (Semi-log) and transition parameter γ = 3.04. The graph suggests that the change from low inflation regime to high inflation regime is relatively gradual. The estimated threshold value of 2.059 points to the half-way of the transition.
5.3Estimation results of PSTR and GMM-IVThe estimation of PSTR needs testing no remaining linearity. Table 6 displays the testing of no remaining non-linearity. We have strong evidence on the existence of one threshold in the model. In the case (1), the hypothesis without threshold (r=0) is rejected at the 1% significance for two tests. In the case (2), the hypothesis with at least two thresholds (r=2) is also rejected. This means that in the context of the ASEAN-5 countries, the relationship between inflation and growth has only one threshold or two regimes.
LM and LR test of no remaining linearity.
| Hypothesis | Test | Statistics | P-value |
|---|---|---|---|
| (1)H0:r=0;H1:r=1 | Lagrange multiplier (LM) | 6.18 | 0.000*** |
| Likelihood-ratio test (LR) | 26.09 | 0.000*** | |
| (2)H0:r=1;H1:r=2 | Lagrange multiplier (LM) | 0.88 | 0.513 |
| Likelihood-ratio test (LR) | 6.05 | 0.533 |
Note: (***) denotes significance at 1%.
Author's estimation using STATA 13.
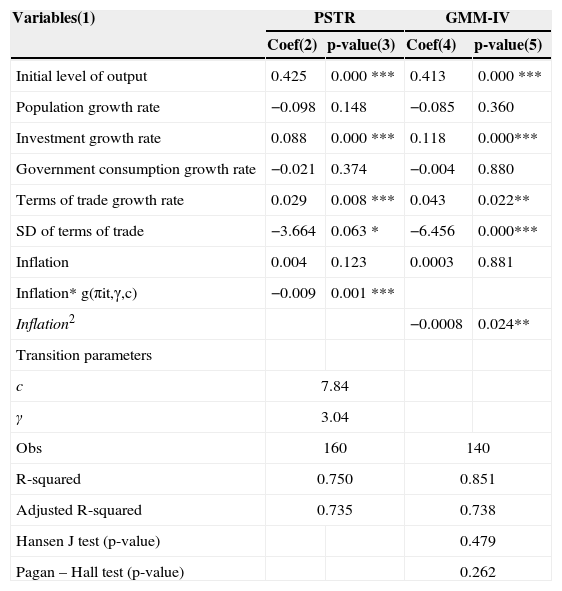
We employ the estimation of PSTR by applying nonlinear least squares to data eliminated the individual effects. Table 7 presents the estimation of PSTR in column 2 and 3 for the ASEAN-5 countries over the period of 1980-2011. We find that the effect of inflation on growth is non-linear. For low inflation regime, inflation coefficient is estimated to be 0.004 and not statistically significant. For high inflation regime, inflation coefficient is found to be −0.009 and statistically significant at 1%. The threshold level of 7.84% is higher than the threshold level of 5.43% for Asian developing economies in Asia found by Vinayagathasan (2013). However, the estimated inflation threshold value for the ASEAN-5 countries is lower than findings in some previous and current empirical studies for developing countries: the threshold value of 12% estimated by Khan and Senhadji (2001), and Baglan and Yoldas (2014); 12.3% calculated by Bick (2010), 10.2%-14.5% detected by López-Villavicencio and Mignon (2011), 10%-12.95% identified by Eggoh and Khan (2014), and 18.9% level for the SADC region estimated by Seleteng et al. (2013).
PSTR and GMM-IV estimation (Dependent variable: Growth rate of GDP).
| Variables(1) | PSTR | GMM-IV | ||
|---|---|---|---|---|
| Coef(2) | p-value(3) | Coef(4) | p-value(5) | |
| Initial level of output | 0.425 | 0.000 *** | 0.413 | 0.000 *** |
| Population growth rate | −0.098 | 0.148 | −0.085 | 0.360 |
| Investment growth rate | 0.088 | 0.000 *** | 0.118 | 0.000*** |
| Government consumption growth rate | −0.021 | 0.374 | −0.004 | 0.880 |
| Terms of trade growth rate | 0.029 | 0.008 *** | 0.043 | 0.022** |
| SD of terms of trade | −3.664 | 0.063 * | −6.456 | 0.000*** |
| Inflation | 0.004 | 0.123 | 0.0003 | 0.881 |
| Inflation* g(πit,γ,c) | −0.009 | 0.001 *** | ||
| Inflation2 | −0.0008 | 0.024** | ||
| Transition parameters | ||||
| c | 7.84 | |||
| γ | 3.04 | |||
| Obs | 160 | 140 | ||
| R-squared | 0.750 | 0.851 | ||
| Adjusted R-squared | 0.735 | 0.738 | ||
| Hansen J test (p-value) | 0.479 | |||
| Pagan – Hall test (p-value) | 0.262 | |||
Note: (***), (**) denote significance at 1% and 5%, respectively. t statistics in parentheses.
Author's estimation using STATA 13.
Regarding the control variables, we find that a positive relationship between initial level of output and annual growth rate over the period. The coefficient of initial level is significant at 1%. Our results do not support the concept of conditional convergence in the ASEAN-5 countries. This may be due to a fact that these countries have not shared the same technology, the same savings rate and the same depreciation parameter. The coefficient of investment variable is positive and significant at 1% as predicted by the Solow growth model and found in some empirical studies such as Khan and Senhadji (2001), López-Villavicencio and Mignon (2011), and Vinayagathasan (2013). Its positive sign suggests that the governments of ASEAN-5 countries can promote growth by stimulating investment and capital accumulation. Terms of trade positively effects on growth and significant at the 1% level, which is similar to the findings of some recent empirical growth studies for developing countries (Mendoza, 1996; Grimes, 2006; Samimi, Sadeghi, & Sadeghi, 2011). The neoclassical growth theory highlights the important role that terms of trade plays in determining risk and return properties of domestic assets, and hence in determining savings and growth (Mendoza, 1996). The coefficient of standard deviation variable is negative and significant at the 10%. This implies that volatility of trade inversely influences growth in ASEAN-5 countries. We recommend that the governments of ASEAN-5 countries may incorporate to reduce trade risks in order to promote the growth.
In order to check for the robustness of our estimation, we employ GMM-IV procedures to estimate Eq. (9). Using the GMM-IV method, we choose initial growth rate variable as instrumented variable since several unobserved factors influence this variable and the remaining control variables by its own lagged values are instruments. The estimated results are presented in column 4 and 5 of Table 7. We find that all coefficient signs of GMM-IV estimation are consistent with those of PSTR estimation. To examine the validity of our instruments, we apply Hansen's J test, where the null hypothesis is that the instruments as a group are exogenous. The p-values of the Hansen J statistics fail to reject the null hypothesis, implying that our instrument set is robust. Moreover, the Pagan–Hall statistic indicates that the residuals from the estimated equations are normally distributed.
6ConclusionFew studies have been published on the relationship between government size and economic growth in ASEAN. This study examines the nexus between inflation and growth for ASEAN countries by applying a smooth transition regression model for panel data (PSTR) and GMM-IV specification. We use a panel of the ASEAN-5 countries for the period 1980-2011. We estimate the threshold value and slope coefficients through the use of endogenous regressors selected from the studies of Barro (1991), Sala-i-Martin (1997), Khan and Senhadji (2001), López-Villavicencio and Mignon (2011), and Baglan and Yoldas (2014): initial level in growth, employment growth rate, investment growth rate, government spending growth rate, growth rate of terms of trade and standard deviation of terms of trade. According to the test used to estimate the number of thresholds, we find that the model with one threshold or two regimes adequately captures this relationship.
Estimated results provide strong evidence that the relationship between inflation and growth is non-linear. The estimated threshold for the inflation rate for the ASEAN-5 countries is 7.84% and statistically significant at the 1% level both PSTR and GMM-IV estimation.
- •
The threshold value of 7.84% is higher than the threshold value of 5.43% for the Asian countries detected by Vinayagathasan (2013). The results are various since there are different from the model specification and data.
- •
This threshold value is lower than the 18.9% level for the SADC region estimated by Seleteng et al. (2013), 10% - 12.9% level for upper and lower middle income countries estimated by Eggoh and Khan (2014) and 12% for developing countries calculated by Baglan and Yoldas (2014). This may be due to the fact that the ASEAN economies have high and stable economic growth for a sustained period and have adopted consistent policy in the country, leading to low and stable inflation rates (Cheng, 1999). Macroeconomic policies have been, on balance, more consistent over time in ASEAN countries. Therefore, the ASEAN countries are generally considered to have had low inflation rates relative to other emerging markets (Jiranyakul & Opiela, 2010).
Besides, we also find that the estimated coefficients associated with the control variables used in the model are consistent with the empirical literature. The speed of transition is relatively smooth. This suggests that central banks in the ASEAN countries should act fast when inflation is near or above the estimated threshold. In summary, the results suggest that central banks could improve economic growth by reducing inflation when it is above or near the estimated threshold value. Central banks in the ASEAN countries may consider a rate of approximately 7.84% as an inflation targeting for maintaining economic stability. To improve regional inflation and growth performance, governments in the region should enhance and coordinated their individual monetary, fiscal and exchange rate polices accordingly (Ayres, Belasenm, & Kutan, 2014).