Si bien es amplia la literatura que se ha dedicado a estudiar los hechos estilizados en las series de los rendimientos, para el caso colombiano solamente existe un trabajo que documenta estos hechos. Alonso y Arcos (2006) documentaron la presencia de cuatro hechos estilizados en la serie de los rendimientos de la tasa de cambio y del principal índice accionario colombiano, empleando una muestra de rendimientos diarios para el período comprendido entre el 21 de enero de 1999 y el 31 de abril de 2005.
Este documento tiene como objetivo continuar el estudio de la existencia de hechos estilizados en el comportamiento de los rendimientos del índice general de la Bolsa de Valores de Colombia (IGBC). El estudio demuestra la existencia de cinco hechos estilizados en el comportamiento de esa serie en sus primeros 10 años. Para lograr este fin, se emplea una batería amplia de pruebas estadísticas que permiten brindar evidencia de la existencia de los siguientes hechos estilizados: I) No se presenta eficiencia suave del mercado; II) colas pesadas de la distribución de los rendimientos; III) normalidad agregada de la distribución de los rendimientos, IV) volatilidad no constante y agrupada de los rendimientos y V) efecto Taylor. Para el estudio se emplea una muestra del IGBC diario para los primeros años de transacciones; es decir, el período comprendido entre el 3 de julio de 2001 y el 5 de julio de 2011.
There are many studies published in the literature on stylized facts in financial time series. However, for the Colombian case there is only one work that documents the stylized facts of the returns. Alonso and Arcos (2006) documented the presence of four stylized facts in the exchange rate series and the principal Colombian Stock Exchange Index (IGBC), using a daily sample for the period from January 21, 1999 to April 31, 2005.
The aim of this document is to present five stylized facts on the behavior of the IGBC returns in its first 10 years. Furthermore, a wider range of statistical test is used to support the existence of those stylized facts. Evidence is provided for the following stylized facts: I) no efficiency of the market; II) heavy tails of the distribution; III) aggregational Gaussianity; IV) volatility clustering and V) Taylor effect. In our case, the sample of the daily IGBC will be used for the period between July 3, 2001 and July 5, 2011.
El 3 de julio de 2011, la Bolsa de Valores de Colombia (BVC) cumplió sus primeros 10 años de actividad, después de la fusión de las tres bolsas existentes en ese momento: la Bolsa de Bogotá creada en 1929, la Bolsa de Medellín, en 1961 y la Bolsa de Occidente (Cali) creada en 1983. Atendiendo a estos diez años, el presente artículo se propone analizar algunas características estadísticas presentes en la serie de los rendimientos del índice general de la Bolsa de Valores de Colombia (IGBC) que comparte con el comportamiento de índices de otras bolsas de valores en el mundo.
De hecho, la literatura financiera ha documentado la existencia de regularidades empíricas de las series de rendimientos de activos (o portafolios) financieros, que en la mayoría de los casos se encuentran presentes sin importar el mercado en que sean transados o el tipo de activo. Estas regularidades empíricas se conocen en la literatura especializada como hechos estilizados1, y son importantes al momento de, por ejemplo, evaluar el riesgo asociado a este portafolio o el comportamiento de largo plazo de este, así como para aquellos actores del mercado que transan regularmente en él.
Sewell, 2011 presenta una revisión exhaustiva de la literatura empírica sobre los hechos estilizados de las series financieras de tiempo en distintos lugares del mundo. La literatura identifica hechos estilizados con relación a la distribución de los rendimientos, la volatilidad y la relación de la autocorrelación de los rendimientos absolutos y los rendimientos al cuadrado, entre otros. Sewell, 2011 detectó que dichos hechos estilizados han sido documentados para distintos países como el Reino Unido, Estados Unidos, Italia, Grecia, Francia y diferentes países asiáticos.
Con respecto a la distribución, algunos autores como Mitchell (1915), Bollerslev et al. (1993), Mantegna y Stanley (2000), Cont (2001), Andreou et al. (2001), Taylor (2005) y Alonso y Arcos (2006) encontraron, para diferentes activos y diferentes períodos y países, que la distribución de los retornos tiende a ser acampanada pero no normal (leptocúrtica).
Con relación a la volatilidad, Houthakker (1961), Mandelbrot (1963), Engle et al. (1990), Bollerslev et al. (1993), Andersen y Bollerslev (1998), Andersen et al. (2001) y Alonso y Arcos (2006) encontraron que grandes cambios en los retornos tienden a ser seguidos por grandes cambios, y pequeños cambios tienden a ser seguidos por pequeños cambios.
En relación con la dependencia o autocorrelación de los rendimientos o una función de estos, Sewell, 2011 concluye que, en resumen,–después de revisar Fama (1970), Ball y Kothari (1989), Lo y Mackinlay (1988), Lo y MacKinlay (1990), entre otros–los retornos semanales y mensuales de las acciones tienen correlación negativa débil y los retornos de los índices diarios, semanales y mensuales están positivamente correlacionados.
Sobre el comportamiento no estacionario de las series de los rendimientos (camino aleatorio), se encuentran autores como Kendall (1953), Houthakker (1961) y Osborne (1962). Y, finalmente, sobre el volumen efecto día o efecto hora, Jain y Joh (1988) encontraron que hay una diferencia significativa en el volumen transado durante las horas del día y a lo largo de los días de la semana.
Si bien es amplia la literatura que se ha dedicado a estudiar los hechos estilizados en las series de los rendimientos, para el caso colombiano solamente existe un trabajo que documenta los hechos estilizados de los rendimientos. Alonso y Arcos (2006) documentaron la presencia de cuatro hechos estilizados en la serie de los rendimientos de la tasa de cambio y del principal índice accionario, empleando una muestra de rendimientos diarios para el período del 21 de enero de 1999 al 31 de abril de 2005. El primer hecho estilizado que documentan los autores es que las series de los activos financieros presentan un comportamiento de camino aleatorio. La evidencia en favor de este hecho son pruebas de raíces unitarias como la ADF, la de Phillips y Perron (1988), KPSS (Kwiatkowski et al. (1992)) y la prueba no-paramétrica de raíces unitarias de Breitung, 2002. El segundo y tercer hechos que discuten Alonso y Arcos (2006) están relacionados con las colas pesadas de la distribución de los rendimientos y la normalidad agregada, para lo cual proveen evidencia gráfica y una prueba de normalidad (Jarque-Bera). Y el cuarto hecho estilizado corresponde a la volatilidad no constante y agrupada para la cual los autores emplean gráficas para comentar este hecho.
El objetivo de este documento es demostrar la presencia de cinco hechos estilizados en el comportamiento de los rendimientos del IGBC en sus primeros 10 años. Adicionalmente, este documento introduce una mejora a la aproximación de Alonso y Arcos (2006) al incluir una batería de pruebas estadísticas para demostrar la presentación de los hechos estilizados en el comportamiento de los rendimientos del IGBC parar los 10 primeros años de la Bolsa de Valores de Colombia. Los hechos estilizados que consideraremos son los más documentados en la literatura, a saber: I) No se presenta eficiencia suave del mercado; II) colas pesadas de la distribución de los rendimientos; III) normalidad agregada de la distribución de los rendimientos; IV) volatilidad no constante y agrupada de los rendimientos y V) efecto Taylor. En nuestro caso, emplearemos la muestra del IGBC diario para los primeros diez años de transacciones; es decir, el período comprendido entre el 3 de julio de 2001 y el 5 de julio de 2011.
Este documento se organiza de la siguiente manera: La primera sección corresponde a esta breve introducción. La segunda sección discute unas generalidades del índice, como su composición, la concentración de la canasta y las mayores pérdidas que ha presentado el índice. De la tercera a la octava sección se discute cada uno de los hechos estilizados enumerados arriba. El documento concluye con unos comentarios finales.
2Generalidades del índiceDesde el año 2001, las empresas que participaban en la Bolsa de Valores de Colombia fueron aquellas que ya se encontraban transando en las Bolsas de Bogotá, Medellín y de Occidente, además de empresas nuevas que decidieron incursionar en el intercambio y negociación de activos financieros. El IGBC corresponde a un índice conformado por una canasta de compañías que participan en la Bolsa de Valores de Colombia; de distintos sectores económicos como el de alimentos, de la construcción, el sector financiero, entre otros.
El índice refleja el comportamiento de un conjunto de acciones representativas para el respectivo mercado accionario. En este orden de ideas, el cálculo de la estructura del índice se efectúa de manera trimestral y el número de empresas incluidas en el índice es variable. La inclusión de una acción en el índice se basa en criterios como la liquidez o rotación de la acción y la frecuencia de negociación (Alonso y Berggrun, 2010).
Así, para el año 2001, el IGBC estuvo conformado principalmente por Cementos Argos SA y Bavaria SA. En ese momento, la canasta estaba conformada por 17 empresas. Mientras que en el año 2011, para los 10 años de la Bolsa, el IGBC era integrado por 35 empresas. En el año 2001, la empresa con mayor participación era Bavaria, con una participación de 38.9%, seguida de Argos y Coltabaco con una participación de 18.1% y 4.9%, respectivamente. En el 2011, las de mayor peso eran Pacific Rubiales Energy Corp SA (PREC), con un 23.7%, Ecopetrol SA, con una participación de 19.3% y Bancolombia SA con un 8.5% (ver fig. 1).
Los 10 años del IGBC parecen evidenciar una disminución de concentración en las transacciones de la Bolsa de Valores de Colombia. Para explorar este punto, podemos emplear el índice Hirschman-Herfindahl (IHH). Este permite determinar qué tan concentrada se encuentra la estructura del índice o mercado estudiado (ver tabla 1). En el año 2001, este índice alcanzó el valor de 0.20, implicando una estructura moderadamente concentrada. Dicha concentración cayó para el final del período estudiado a 0.11, lo que implica una estructura no concentrada. Sin embargo, es interesante observar lo ocurrido con la concentración del índice durante este período. A partir de 2002, el IHH mostró una estructura no concentrada, alcanzando el menor índice de concentración de 0.07 en el año 2004. Y en el año 2009 el IHH alcanzó el máximo valor de los diez años (0.21), posiblemente explicado por el ingreso de Ecopetrol a la Bolsa de Valores de Colombia. Esa estructura no concentrada se mantiene hasta 2007, cuando el IHH alcanzó el valor de 0.10. La estructura moderadamente concentrada se presentó hasta 2009, cuando la misma regresó a ser no concentrada (ver tabla 2 y fig. 2).
Drawdowns del IGBC en sus primeros 10 años (de mayor a menor)
| Desde | Tocando fondo | Hasta | Profundidad | En días | ||
| Longitud | Caída | Recuperación | ||||
| 30-01-2006 | 27-10-2008 | 26-07-2010 | -50.34% | 1089 | 668 | 421 |
| 12-07-2001 | 08-11-2001 | 28-12-2001 | -23.76% | 115 | 81 | 34 |
| 28-04-2004 | 13-05-2004 | 14-09-2004 | -21.85% | 94 | 12 | 82 |
| 08-11-2010 | 05-05-2011 | -16.14% | 163 | 122 | NA | |
| 25-02-2005 | 15-03-2005 | 23-06-2005 | -14.83% | 79 | 13 | 66 |
Cálculos propios
Por otra parte, en la figura 3 se puede observar la serie del IGBC, sus rendimientos y el histograma de los rendimientos para el período analizado. En principio, esta gráfica muestra un comportamiento típico de un activo financiero. Es decir, presenta el comportamiento típico que se ha denominado “hechos estilizados”2. Por ejemplo, períodos de alta o baja volatilidad en los rendimientos van seguidos de períodos similares. Por otro lado, la distribución de los rendimientos si bien presenta una forma acampanada, esta es bastante picuda y presenta colas relativamente pesadas.
En la figura 4 se presentan los principales drawdowns del IGBC. Un drawdown es una medida de cuánto cae un precio o un índice desde su máximo más reciente. Esta medida es ampliamente empleada como parámetro de qué tan riesgoso es un portafolio. El máximo drawdown se presentó entre el 30 de enero de 2006 y el 26 de julio de 2010, cuando el índice cayó hasta tocar fondo el 27 de octubre de 2008, y tardó 421 días de negociación para lograr el mismo nivel del 30 de enero de 2008. En total, la caída hasta el peor momento fue del 50.34%. Otros tres drawdowns se presentaron en los primeros 10 años del IGBC comprendidos entre el 12 de julio de 2001 y el 28 de diciembre del mismo año, entre el 20 de abril de 2004 y el 14 de noviembre de 2004 y entre el 25 de febrero de 2005 y el 15 de marzo del mismo año (ver tabla 2). Al final del período de estudio, el IGBC estaba experimentando un drawdown, pero aún no había alcanzado a recuperar el valor experimentado el 8 de noviembre de 2010 para el corte de nuestra muestra.
En las siguientes secciones nos concentraremos en brindar evidencia sobre los hechos estilizados que presenta el comportamiento del IGBC.
3Hecho estilizado 1: No eficiencia suave del mercadoEl primer hecho estilizado está relacionado con la hipótesis que los precios de los activos (o valor de un portafolio) sigue un camino aleatorio. En otras palabras, el cambio en el precio (valor del portafolio) no es predecible. En los mercados emergentes, se ha encontrado que no existe este comportamiento de camino aleatorio (ver, por ejemplo, Karemera et al., 1999; Worthington y Higgs, 2003; Kim y Shamsuddin, 2008 y Urrutia, 1995)
Esta hipótesis comúnmente se define en términos del rendimiento de los activos (portafolios), pues es equivalente considerar que la historia de los rendimientos no es relevante a la hora de predecir el retorno para el siguiente período. Este comportamiento es lo que se conoce como la hipótesis de la eficiencia suave de los mercados financieros.
De hecho, el comportamiento de camino aleatorio implicará un comportamiento estacionario de los rendimientos. Y esto, a su vez, implica que los rendimientos seguirán un proceso con varianza constante. Como se discutirá más adelante, este supuesto no tiene mucho sentido cuando se trata de rendimientos financieros. Formalmente, un modelo Martingala es una versión generalizada del camino aleatorio que permite un comportamiento heteroscedástico.
Así, el precio de un activo sigue un proceso de martingala cuando su rendimiento es puramente impredecible, de tal manera que los inversionistas no podrán obtener rendimientos anormales por períodos prolongados.
Para probar la hipótesis de la eficiencia suave del mercado que representa el IGBC, emplearemos 14 diferentes pruebas. Todas tienen en común que la hipótesis nula será:
- –
H0: rtno está autocorrelacionado
- 1.
Test automático de Portmanteau (Escanciano y Lobato, 2009)
- 2.
Test automático de proporción de la varianza (Choi, 1999)
- 3.
Test del promedio exponencial (Andrews y Ploberger, 1996)
- 4.
Test transformado de proporción de la varianza (Chen y Deo, 2006)
- 5.
Test de proporción de la varianza (Lo y MacKinlay, 1988)
- 6.
Test bootstrapping (Choi, 1999 y Kim, 2006)
- 7.
Test de proporción de la varianza múltiple (Chow y Denning, 1993)
- 8.
Test martingala para diferencia de hipótesis (Domínguez y Lobato, 2003)
- 9.
Test espectro generalizado (Escanciano y Velasco, 2006)
- 10.
Test de rango y signo conjuntos de Wright (Belaire-Franch y Contreras, 2004)
- 11.
Test para una caminata aleatoria (Choi, 1999 y Durlauf, 1991)
- 12.
Test de submuestreo (Whang y Kim, 2003)
- 13.
Test Wald (Richardson y Smith, 1991)
- 14.
Test de signo y rango (Wright, 2000)
Los resultados de estas pruebas con sus diferentes variantes se presentan en la tabla 3. En todos los casos podemos rechazar la hipótesis de una eficiencia suave (no autocorrelación); este resultado es igual al obtenido en buena parte de países asiáticos (ver, por ejemplo, Kim y Shamsuddin, 2008; Lovato y Velasco, 2000).
Pruebas para un camino aleatorio
| Prueba de normalidad | Estadístico | |
| Portmanteau/Escanciano, J.C., y Lobato, I.N. (2009) | 9.0333 | *** |
| Bootstrapping - Normal/Choi (1999) | 5.7999 | *** |
| Bootstrapping - Manmen/Choi (1999) | 5.7999 | *** |
| Bootstrapping - Rademacher/Choi (1999) | 5.7999 | *** |
| LR/Andrews y Ploberger (1996) | 31.1428 | *** |
| LM/Andrews y Ploberger (1996) | 30.3214 | *** |
| QPn/Chen y Deo (2006) | 8.5894 | *** |
| M1 (2 días)/Lo y MacKinlay (1988) | 7.6919 | *** |
| M2 (2 días)/Lo y MacKinlay (1988) | 3.0047 | *** |
| M1 (5 días)/Lo y MacKinlay (1988) | 6.3040 | ** |
| M2 (5 días)/Lo y MacKinlay (1988) | 2.4733 | ** |
| M1 (10 días)/Lo y MacKinlay (1988) | 4.1063 | * |
| M2 (10 días)/Lo y MacKinlay (1988) | 1.7249 | * |
| CD1/Chow y Dening (1993) | 7.6919 | *** |
| CD2/Chow y Dening (1993) | 3.0047 | *** |
| DL/Dominguez y Lobato (2003) | 10.9576 | *** |
| Pboot/Escanciano, J.C. y Velasco, C. (2006) | N.A. | *** |
| JR1/Belaire-Franch G, y Contreras D. (2004) | 10.6489 | *** |
| JR2/Belaire-Franch G, y Contreras D. (2004) | 10.0405 | *** |
| JS1/Belaire-Franch G, y Contreras D. (2004) | 9.3376 | *** |
| AD/Durlauf (1991) y Choi (1999) | 29.3638 | *** |
| Bloque 75/Whang y Kim (2003) | N.A. | *** |
| Bloque 125/Whang y Kim (2003) | N.A. | *** |
| Bloque 175/Whang y Kim (2003) | N.A. | *** |
| Bloque 225/Whang y Kim (2003) | N.A. | ** |
| Bloque 275/Whang y Kim (2003) | N.A. | ** |
| Bloque 325/Whang y Kim (2003) | N.A. | ** |
| Wald/Richardson y Smith (1991) | 62.2677 | *** |
| R1 (2 días)/Wright (2000) | 10.6489 | *** |
| R2 (2 días)/Wright (2000) | 10.0405 | *** |
| S1 (2 días)/Wright (2000) | 9.3376 | *** |
| R1 (5 días)/Wright (2000) | 8.1354 | *** |
| R2 (5 días)/Wright (2000) | 7.8033 | *** |
| S1 (5 días)/Wright (2000) | 7.7713 | *** |
| R1 (10 días)/Wright (2000) | 6.3436 | *** |
| R2 (10 días)/Wright (2000) | 5.8809 | *** |
| S1 (10 días)/Wright (2000) | 7.1162 | *** |
Cálculos propios.
N.A. = En este caso el estadístico no aplica. La decisión se basa en un ejercico de bootstraping con 500 repeticiones.
Este resultado implica que los rendimientos presentan un comportamiento que puede ser explicado, en parte, por comportamientos pasados de esa misma serie. En otras palabras, la serie de los rendimientos contiene información que puede, en parte, determinar cuál será el comportamiento futuro de los rendimientos del IGBC. Así, la hipótesis de la eficiencia suave de este mercado no es soportada por el comportamiento de los rendimientos del IGBC para sus diez primeros años de existencia. Este resultado es común en los mercados financieros y constituye el primer hecho estilizado que presenta el IGBC en sus primeros 10 años. Este hecho estilizado tiene implicaciones sobre la predictibilidad de los rendimientos del IGBC.
4Hecho estilizado 2: Distribución acampanada pero no normal (colas pesadas de la distribución)La distribución (no condicional) de los rendimientos financieros comúnmente presenta características similares a la distribución normal, en especial su simetría y forma acampanada; pero esta tiende a ser más “picuda” y tener colas más pesadas que la distribución normal. La figura 5 muestra el histograma de los rendimientos con la correspondiente distribución normal sobrepuesta (línea sólida). En el centro se observa una distribución más picuda que la normal y las colas son más pesadas que la normal (ver, por ejemplo, Liesenfeld y Jung, 2000; David, 1997; Lux y Sornette, 2002).
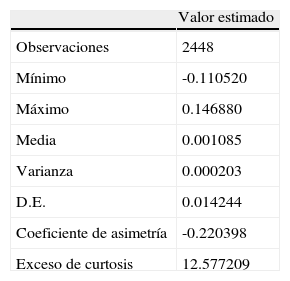
Así, la distribución de los rendimientos diarios parece ser leptocúrtica y presentar colas pesadas. Estas observaciones se pueden corroborar con las correspondientes estadísticas descriptivas que se reportan en la tabla 4. La curtosis es mucho más grande que aquella de la distribución normal y el coeficiente de asimetría es cercano a cero, de tal manera que se puede considerar como una distribución simétrica.
Por otro lado, podemos emplear pruebas de normalidad para determinar si estos datos corresponden o no a una distribución normal. Por ejemplo, usaremos las pruebas de:
- 1.
Test de normalidad Shapiro-Wilk
- 2.
Test de normalidad Kolmogorov-Smirnov
- 3.
Test de normalidad Pearson
- 4.
Test de normalidad Jarque Bera
- 5.
Test de normalidad Anderson-Darling
- 6.
Test de normalidad Cramer Von Mises
- 7.
Test de normalidad Shapiro-Francia
- 8.
Test de normalidad Doornik-Hansen (Independencia)
- 9.
Test de normalidad Doornik-Hansen (Dependencia débil)
- 10.
Test de normalidad Ruido Blanco
En la tabla 5 se reportan dichas pruebas para el caso de los primeros 10 años de rendimientos diarios del IGBC. Estas pruebas permiten concluir que la distribución empírica de los rendimientos diarios se distancia de la distribución normal.
Pruebas de normalidad para los rendimientos diarios del IGBC
| Prueba | Estadístico | |
| Prueba Shapiro-Wilk | 0.881 | *** |
| Prueba Kolmogorov-Smirnov | 0.090 | *** |
| Pearson chi-square | 387.829 | *** |
| Jarque Bera | 16187.525 | *** |
| Anderson-Darling | Inf | *** |
| Cramer-von Mises | 8.245 | *** |
| Shapiro-Francia | 0.879 | *** |
| Doornik-Hansen (Independencia) | 3241.539 | *** |
| Doornik-Hansen (Dependencia débil) | 3236.847 | *** |
| Ruido Blanco | -1.462 | ** |
Cálculos propios.
*Se puede rechazar la hipótesis nula de normalidad con un 90% de confianza.
De esta manera, el segundo hecho estilizado del comportamiento de los rendimientos del IGBC implica que, si bien su distribución tiene forma acampanada, no constituye una distribución normal. Este hecho estilizado tiene implicaciones importantes, por ejemplo, sobre los supuestos al momento de calcular medidas de riesgo como el Valor en Riesgo (VaR por su nombre en inglés).
5Hecho estilizado 3: Normalidad agregadaUna característica interesante que presentan algunas series de los rendimientos de los activos es que si bien su distribución no es normal–como se discutió anteriormente–, a medida que los rendimientos se calculan para períodos más grandes, la distribución de ellos tiende a parecerse más a una distribución normal (si bien no necesariamente seguirán dicha distribución). En otras palabras, la forma de la distribución de los rendimientos no es la misma para diferentes escalas de tiempo. Este fenómeno se conoce con el nombre de normalidad agregada (ver, por ejemplo, Nelson, 1991).
Este hecho estilizado implica que si se compara la distribución de los rendimientos diarios con la de los rendimientos semanales, mensuales y trimestrales, se encontrará que estos últimos tienen un comportamiento más cercano al de una distribución normal.
En el tabla 6 se puede observar cómo la distribución de los rendimientos trimestrales presentan un exceso de curtosis relativamente menor que los rendimientos para el mismo activo, pero para períodos de agregación de mayor frecuencia. Por otro lado, las pruebas de normalidad y el gráfico QQ (ver fig. 6) corroboran que la hipótesis de no normalidad no se puede rechazar para los rendimientos calculados para un período trimestral. Este resultado gráfico también se puede comprobar empleando las mismas 10 pruebas de normalidad que se emplearon anteriormente. En la tabla 7 se presentan los resultados para las pruebas de normalidad para diferentes períodos de agregación. Cuando se consideran rendimientos para un período de tres meses, la hipótesis nula de normalidad no se puede rechazar con ninguna de las 10 pruebas. Por otro lado, los estadísticos de prueba muestran como a medida que se aumenta el período de agregación, estos están más cerca de no rechazar la nula de una distribución normal.
Estadísticas descriptivas de los rendimientos del IGBC para diferentes períodos
| Diarios | Semanales | Mensuales | Trimestrales | |
| Observaciones | 2448 | 502 | 119 | 39 |
| Mínimo | –0.110520 | –0.204962 | –0.246767 | –0.226312 |
| Máximo | 0.146880 | 0.092125 | 0.178431 | 0.433086 |
| Media | 0.001085 | 0.005251 | 0.022393 | 0.068899 |
| Varianza | 0.000203 | 0.001114 | 0.005532 | 0.021800 |
| D.E. | 0.014244 | 0.033371 | 0.074376 | 0.147650 |
| Coeficiente de asimetría | –0.220398 | –1.264746 | –0.589010 | 0.063124 |
| Exceso de curtosis | 12.577209 | 7.101503 | 1.502351 | –0.213785 |
Cálculos propios.
Prueba de normalidad para los rendimientos del IGBC de diferentes períodos
| Prueba | Diarios | Semanales | Mensuales | Trimestrales | |||
| Estadístico | Estadístico | Estadístico | Estadístico | ||||
| Prueba Shapiro-Wilk | 0.881 | *** | 0.907 | *** | 0.955 | *** | 0.985 |
| Prueba Kolmogorov-Smirnov | 0.090 | *** | 0.079 | 0.085 | ** | 0.092 | |
| Pearson chi-square | 387.829 | *** | 70.709 | *** | 24.176 | ** | 7.385 |
| Jarque Bera | 16187.525 | *** | 12015.162 | *** | 19.419 | 0.035 | |
| Anderson-Darling | Inf | *** | 7.200 | *** | 1.505 | *** | 0.219 |
| Cramer-von Mises | 8.245 | *** | 1.191 | *** | 0.250 | *** | 0.033 |
| Shapiro-Francia | 0.879 | *** | 0.904 | 0.953 | 0.985 | ||
| Doornik-Hansen (Independencia) | 3241.539 | *** | 133.653 | *** | 10.505 | *** | 0.549 |
| Doornik-Hansen (Dependencia débil) | 3236.847 | *** | 133.182 | *** | 10.281 | *** | 0.466 |
| Ruido Blanco | –1.462 | ** | 0.166 | * | –1.548 | ** | –2.279 |
Cálculos propios.
Estos resultados demuestran la presencia de este hecho estilizado en el IGBC. La distribución de los rendimientos se acerca cada vez más a una distribución normal a medida que el período de agregación aumenta. Este resultado, al igual que el anterior, tiene implicaciones sobre el cálculo de medidas de riesgo como el VaR.
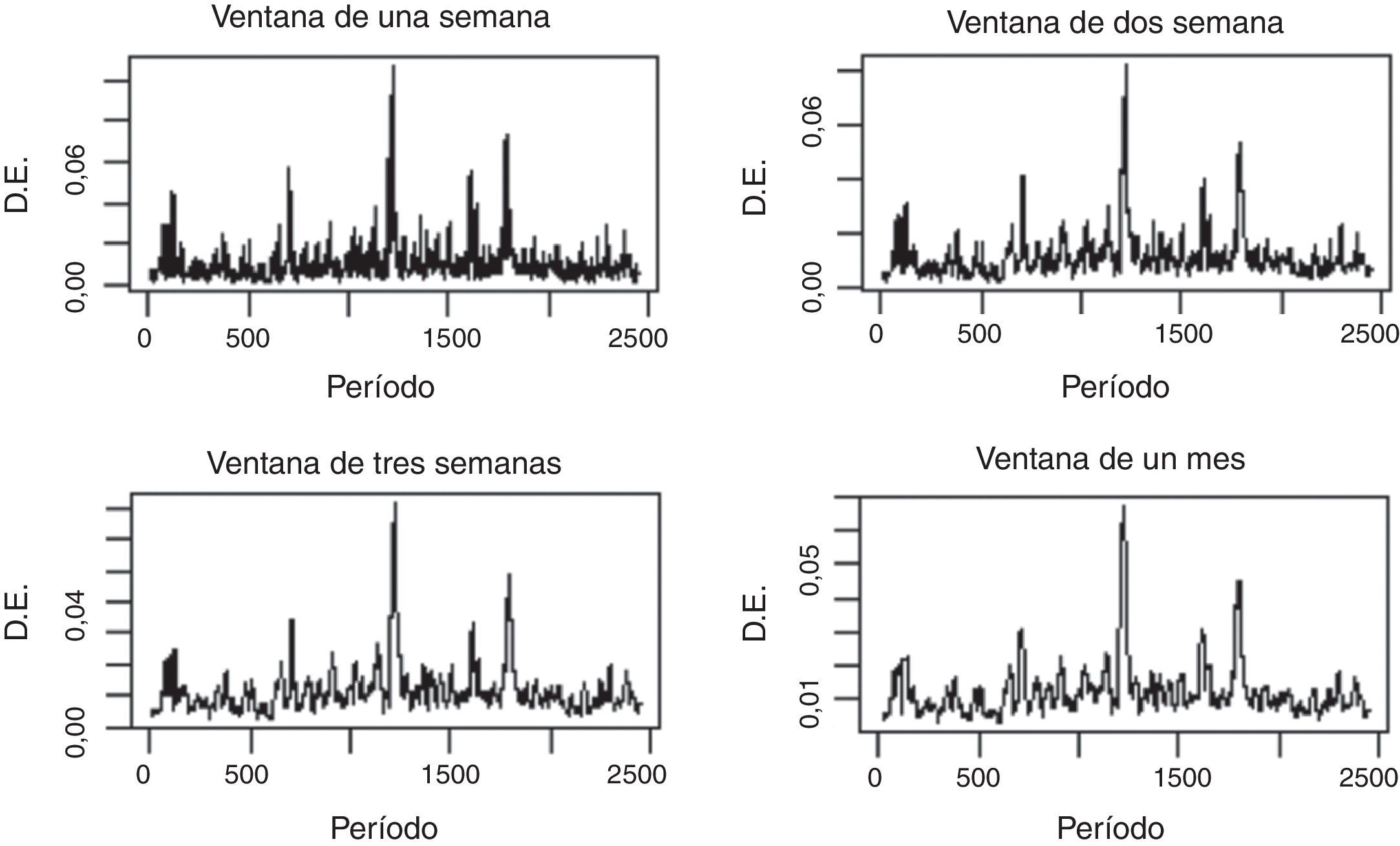
6Hecho estilizado 4: Volatilidad no constante y agrupadaEl cuarto hecho estilizado que consideraremos es que la volatilidad es no constante y se presenta de manera agrupada. Como se puede observar en la figura 7, los rendimientos muestran una gran variabilidad en su volatilidad. En otras palabras, la desviación que ellos presentan respecto de su media es muy cambiante. Pero no solo eso; la volatilidad busca “agruparse” o presenta clusters (volatility cluster, según su nombre en inglés), pues episodios de gran volatilidad tienden a estar seguidos de períodos de alta volatilidad, y viceversa. (Para una discusión más amplia, ver Alonso y Arcos, 2006, y Lux y Marchesi, 2000).
Este hecho estilizado puede ser observado en la serie diaria de rendimientos del IGBC, empleando diferentes medidas de volatilidad. Por ejemplo, para determinar que la varianza no es constante, podemos emplear la desviación estándar calculada para una ventana móvil para diferentes períodos. Esto es, una semana (5 días), dos semanas (10 días), tres semanas (15 días) y un mes. En la figura 7 se puede observar cómo, independientemente de la ventana que se emplee, es posible encontrar que la desviación estándar cambia mucho en el tiempo.
Otra forma de medir la volatilidad (y demostrar que no es constante) que se emplea en la literatura es el cuadrado de los rendimientos o su valor absoluto. Los rendimientos al cuadrado se emplean como medida de volatilidad, dado que los rendimientos diarios comúnmente presentan un promedio estadísticamente igual a cero; entonces, el rendimiento al cuadrado equivale a la dispersión alrededor de la media al cuadrado.
En la figura 8 se presentan estas otras medidas de volatilidad. De modo que, sin importar la medida que se tome, se evidencia que se encuentra el mismo fenómeno: la volatilidad de los rendimientos no es constante. Este hecho estilizado no sorprende y se encuentra ampliamente documentado; la implicación práctica es la necesidad de modelar la varianza de los rendimientos con modelos, por ejemplo, de la familia GARCH.
7Hecho estilizado 5: Efecto TaylorTaylor (1986) encontró que la autocorrelación del valor absoluto de los rendimientos comúnmente es mayor que la autocorrelación del cuadrado de los rendimientos. Granger y Ding (1995) denominaron a esta regularidad “efecto Taylor”. Formalmente, y de manera más general, Granger y Ding (1995) definen el efecto Taylor de la siguiente manera:
Para todo θ≠1. Donde: ρθ(k) representa la autocorrelación muestral de orden k para rtθ, con θ>0. Es más, Granger y Ding (1995) encontraron que la máxima autocorrelación muestral no siempre ocurre cuando θ=1, sino cuando 0<θ<1. También, ellos encuentran que las autocorrelaciones de los retornos absolutos son siempre mayores que las autocorrelaciones de los residuos al cuadrado.
En la figura 9 graficamos la autocorrelación muestral estimada (ρθ(k)) para los primeros 10 rezagos (k = 1... 10) para los rendimientos absolutos del IGBC y después, en la figura 10, el efecto Taylor para los rendimientos al cuadrado. Cada una de las líneas de dichos gráficos representan un rezago diferente y el punto sobre cada una de las líneas muestra la máxima autocorrelación alcanzada. De estos gráficos se puede concluir que esta regularidad empírica se cumple también para la serie analizada.
Es importante notar que tanto el retorno absoluto como el retorno al cuadrado son, convencionalmente, medidas de riesgo del portafolio. Así, el efecto Taylor implica que la medida de riesgo que implica el valor absoluto del retorno tiene una mayor memoria (autocorrelación) que la medida de riesgo que implica el rendimiento al cuadrado.
8Comentarios finalesComo se mencionó anteriormente, está bien documentada en la literatura la existencia de hechos estilizados en el comportamiento de las series de los rendimientos de activos financieros para diferentes mercados y diferentes países. No obstante, para el caso colombiano dichos hechos estilizados no se encuentran documentados extensivamente. Este trabajo ilustra 5 hechos estilizados presentes en la serie de los rendimientos del IGBC en sus primeros 10 años. Nuestras pruebas estadísticas permiten concluir que para el caso del IGBC colombiano también se presentan regularidades en diferentes mercados a nivel internacional. Estas son: I) No se presenta eficiencia suave del mercado; II) colas pesadas de la distribución de los rendimientos; III) normalidad agregada de la distribución de los rendimientos; IV) volatilidad no constante y agrupada de los rendimientos y V) efecto Taylor.
La presencia de dichos hechos estilizados tiene implicaciones interesantes para la modelación y pronóstico del comportamiento del IGBC. Por ejemplo, tener en cuenta estos hechos estilizados podrá mejorar el comportamiento de aproximaciones que midan el riesgo de mercado de portafolios que se comporten como el IGBC. Específicamente, la estimación del VaR podría mejorar al incluir dichos hechos estilizados.
Además, existen otras regularidades presentes en el comportamiento de los activos financieros que merecen ser explorados en futuras investigaciones. Por ejemplo, los denominados efectos calendario, entre los cuales se encuentran el efecto del día de la semana, el de los días festivos y el de los fines de semana.
Finalmente, es importante mencionar que la literatura presenta muy pocos estudios de todas estas regularidades para los países latinoamericanos. Así, existe un gran espacio para investigar la presencia de estas regularidades y sus implicaciones para los reguladores y demás actores de los mercados de valores latinoamericanos.
La expresión “hecho estilizado” es comúnmente empleada por los economistas para referirse a comportamientos regulares que son observados consistentemente en diferentes áreas geográficas y períodos. Estas regularidades son tan consistentes que permiten predecir que ocurrirán. (Ver, por ejemplo, Alonso y Arcos (2006) para una discusión del tema.