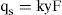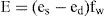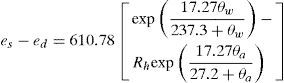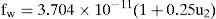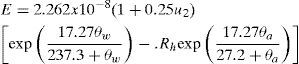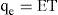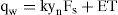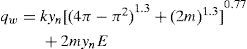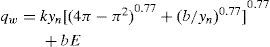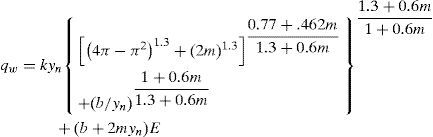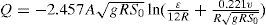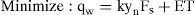Today the increased world population and therefore the growth demand has forced the researchers to investigate better water canal networks distributing much more water while at least keeping its quality. Canal design formulas are explicitly obtained for different cross-sections considering minimum area but optimal design of canal sections considering seepage and evaporation losses are still an open area to study. In this study, two different algorithms are applied to this problem and results are compared with the one in literature. Genetic algorithm and sequential quadratic programming technique are used in optimization. Triangular, rectangular and trapezoidal cross-sections are optimized. It is seen that both algorithms are giving more accurate results than in literature.
Water is the key element of life and its importance for life beings has not changed over the centuries. Even though today there are many investigations and consequently inventions on new kind of materials, a simple solution on using water effectively is still concerned as much important as them [1]. Saving water used in irrigation, cleaning, cooking and even transferring energy is necessary for a sustainable life [2].
Much of the water used by mankind is used in irrigation. Many different irrigation ways are applied over the years but water has been always conveyed and distributed by using canals. Today the increased world population and therefore the growth demand has forced the researchers to investigate better water canal networks distributing much more water while at least keeping its quality. The uncertainty of canal's nature may cause the failure of the canals to convey water during periods of high flow which may lead to the overall failure of many surface water resource systems. Therefore the loss of water from irrigation canals has to be minimized.
Swamee et al. has shown that more than half of the water supplied at the head of the canal is lost in seepage and evaporation by the time water reaches the field [3]. Seepage loss is the important part of the total water loss. In fact, significant part of loss comes from the evaporation however seepage takes place on a canal even respectively at small amount. The correct lining could stop this seepage loss but the change over the time in lining makes the finding correct lining a difficult problem to solve. Even though evaporation loss changes with time whether it is winter or summer and also concrete lining conditions (cracks etc.) affect the seepage loss, they can be estimated under certain conditions. Therefore, design of a canal cross section should be optimized considering minimization of the seepage loss and evaporation loss over the time. In this study, a previously defined canal cross section problem is solved with different techniques.
Minimizing cross section area has already been studied by a few researchers [4]. Different cross section types are concerned: Triangular [5–6], Rectangular [5–6], Trapezoidal [5–9], Parabolic [10–12], Curvilinear Bottomed Channel [13] and Circular [15,21,26,27]. In this study only triangular, rectangular and trapezoidal cross-sections are concerned due they are much widely used as benchmark problems.
Different set of conditions are considered. Guo and Hughes accounted freeboard as input parameter [14]. Aksoy and Altan-Sakarya used Mannig's formula in calculating flow velocity [15]. Bhattacharjya combined the critical flow condition with other conditions [16]. Jain et al. followed Lotter's approach in defining composite canal section [17]. Easa et al. considered the criterion for the side slope stability (soil conditions) [18].
Different optimization methodologies are applied (Direct algebraic technique [19], Complex variables and series expansions [20], Lagrange's method [21–22], Nonlinear optimization techniques [3,23], Sequential quadratic programming [16], Lagrange's undetermined multiplier approach [13], a hybrid model of genetic algorithm and sequential quadratic programming hybrid model [9], genetic algorithm [17], ant colony optimization [24] to design open channels. Adarsh modelled uncertainty [25].
Also different topics are taken as objectives. Trout considered lining material cost [19]. Das minimized the flooding probabilities [8]. However studies concerning the minimum seepage loss are limited in literature. Kacimov merged seepage losses and channel lining [20]. Swamee et al. [26–27] merged earth work and lining cost. Chahar also considered seepage loss [13]. Swamee et al. [3, 23] considered the seepage loss in the objective functions.
This study aimed to simplify the current canal section problem concerning water losses. Equations for seepage loss [5], the evaporation in flowing channels [28], and the resistance in open channel flow [29] are taken from literature. Two different algorithms (Genetic Algorithm and Sequential Quadratic Program) are applied to compare the results with existing literature to evaluate their effectiveness. Minimum water loss sections have been obtained for three different canal sections (triangular, rectangular, and trapezoidal). Following section briefly overviews water loses. Section 3 presents the problem formulation and Section 4 gives brief explanation on the methodology used in the study. Section 5 provides the results and last section presents the research conclusions and future work plans.
2Water lossesWater moves continuously on earth by changing its phase gas to liquid or to solid and vice versa. It flows as rivers and streams, moves in air as clouds and is stored in lakes, in oceans, and sometimes as icebergs. We use dams to store it and canals to distribute to where it is needed. Water continues its movement while distributing to the target place. It evaporates and goes up according to the weather conditions and infiltrates and goes down according to condition of soil where canal is built. So, particular amount of water will be lost in distribution. This section explains how to calculate seepage [5] and evaporation [28] losses and how much resistance [29] occurs in channel.
2.1Water losses due to seepageContinuous seepage from canal may results in local water-logging problem with salt accumulation. There should be regular checking in lining to maintain its proper work but many unavoidable factors will cause the performance of canal gradually decrease even if extreme care is taken [30].
The seepage loss from a canal in a homogeneous and isotropic porous medium when the water table is at very large depth was written as [3]
where qs = seepage discharge per unit length of canal (m2/s); k = hydraulic conductivity of the porous medium (m/s); y = depth of water in the canal (m); F = function of channel geometry (dimensionless); and yF = width of seepage flow at the infinity. Hereafter, F will be referred to as the seepage function.2.2Water losses due to evaporationLoss due to evaporation depends on the many factors. Increase in temperature boosts evaporation. Increase in wind velocity also raises the amount of evaporation. Evaporation is related with the specific humidity gradient in the air and the supplied energy to water. There are many equations in the literature to estimate evaporative rate. These equations can be classified into three categories; (1) energy balance equations; (2) mass transfer equations; and (3) combinations of the two. It is seen that the mass transfer equations are the most appropriate ones for determining evaporation for our problem [28].
The mass transport type equations are expressed as
where E = evaporation discharge per unit free surface area (m/s); es = saturation vapor pressure of the air at the temperature of the water surface (Pa); ed = saturation vapor pressure of the air at the dew point (Pa); and fw = wind function (m/s/Pa). The difference between the saturation vapor pressure of the air at the temperature of water surface and at the dew point (es – ed) in Pa was given by [31].where ¿w = water surface temperature in °C; ¿a = mean air temperature in °C; and Rh = relative humidity expressed as fraction. The wind function for a flowing channel in m/s per Pa was given as [28]:where u2 = wind velocity in m/s at 2 m above the free surface. Combining Eqs. 2-4, E in m/s is obtained as [5]Once E is known the evaporation loss from a canal can be expressed as
where qe = evaporation discharge per unit length of canal (m2/s); and T = width of free surface (m).2.3Total water lossAdding Eqs. 1 and 6, the total water loss qw (m2/s) was expressed as:
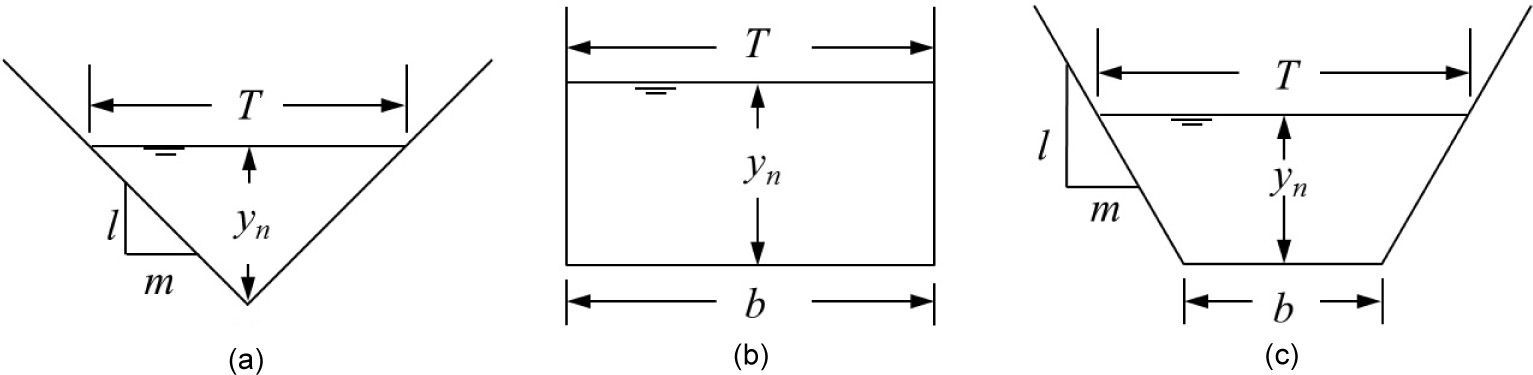
Using the equations [3] for Fs, Eq. 7 for triangular channel section becomes [5]
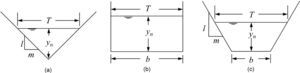
where m=side slope shown in Fig. 1a. Similarly for rectangular section Eq. 7 was changed to [5]where b = bed width of the section shown in Fig. 1b. On the other hand, for trapezoidal section shown in Fig. 1c, Eq. 7 was reduced to [5]2.4Resistance equationResistance of flow in canal is used in design of uniform open canal. Manning's equation is the mostly used formula in design [32], which turbulent flow and relative roughness are taken into account [33]. The equation will be used in this study [29] is:
where Q = canal discharge (m3/s); A = flow area (m2); g = gravitational acceleration (m/s2); R = hydraulic radius (m) defined as the ratio of the flow area to the flow perimeter (A/P) (m); ¿ = average roughness height of the canal lining (m); and v = kinematic viscosity of water (m2/s); S0 = Bed slope.3Design problemDetermination of optimal canal section shape was reduced to;
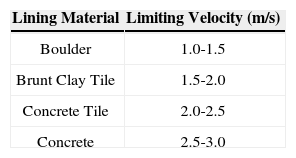
which is the general Eq. 7 of total water loss. Eqs. 8–10 is going to be used for triangular, rectangular and trapezoidal channel sections.where A = flow area (m2); and V = average velocity (m/s). This average velocity has to be less than the limiting velocity. Limiting velocities for the different lining materials are shown in the table below in Table 1[5].In this optimization, concrete lined canal is designed for carrying a discharge of 10m3/s on a longitudinal slope of 0.001. The canal lining has ¿=1mm. Assume canal lining as cracked; and having k=10−6m/s. The maximum evaporation loss E was estimated as 2.5x10−6m/s. The water temperature is 20°C at which v = 1.1x10−6m2/s.limiting velocity, VL, is taken 2.5 m/s.
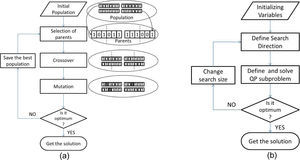
4MethodologyGenetic algorithm and sequential quadratic programming method are applied to solve the problem in this study. Matlab Optimization Toolbox is used as a solver (Fig.2). Standard settings of the toolbox are used except that number of generations is defined as 1000000 instead of 100. This section will only explain the basic of the algorithm. The detailed explanation can be found in literature.
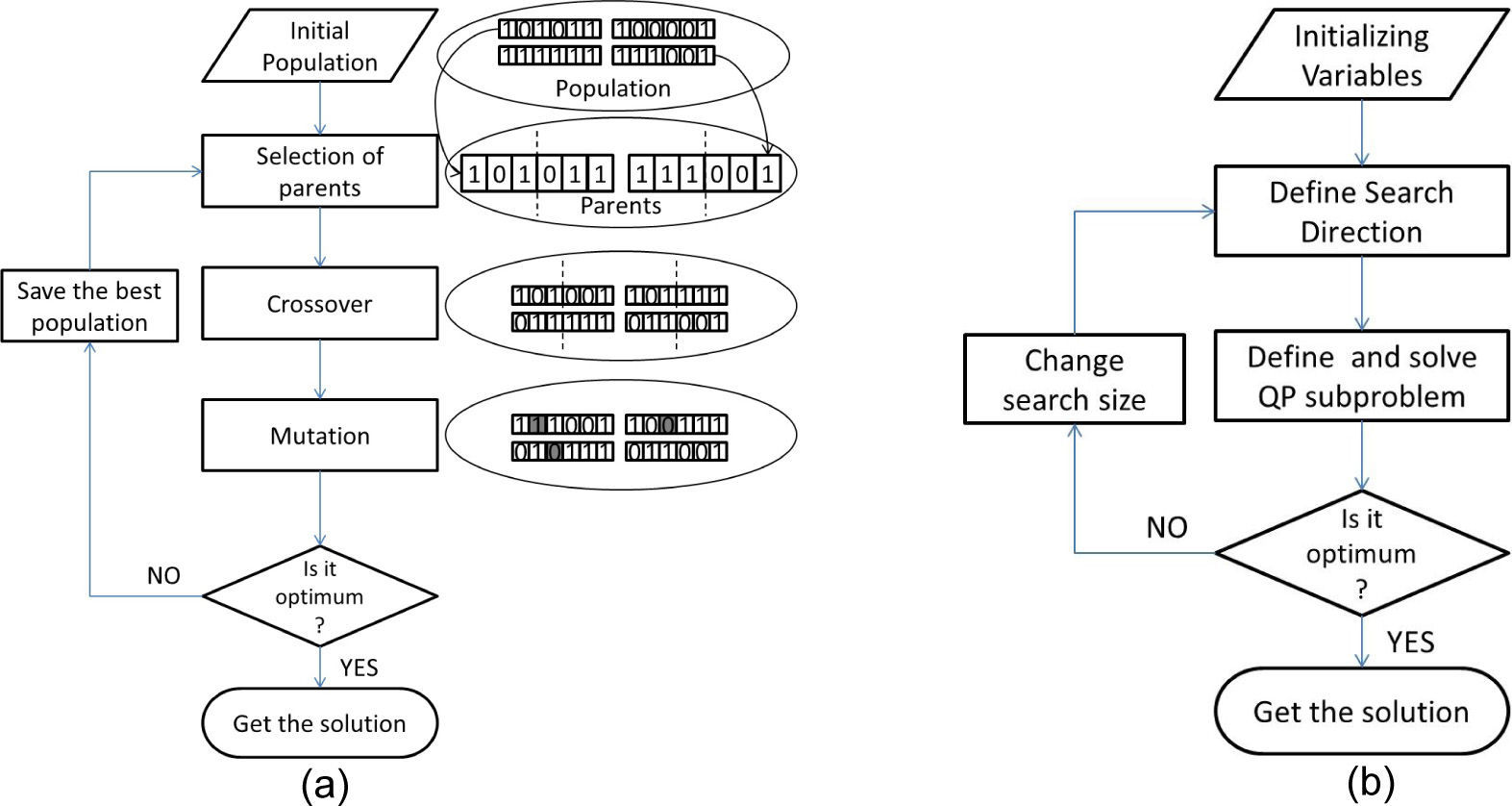
4.1Genetic algorithmGenetic Algorithm is a kind of evolutionary algorithm which becomes popular by the publication of John Holland's book in 1970's [34]. GA is a method for solving optimization problems based on natural selection. It changes the population of solutions in a sequence. At each step, it chooses individuals as parents randomly from the current population. Then, next generation is produced by parents. Over successive generations, the population “evolves” toward an optimal solution. The main advantage of genetic algorithm is the applicability to optimization problems in which the objective function is discontinuous, nondifferentiable, stochastic, or highly nonlinear. Three main steps of GA generate the solutions [35]. Fig. 3(a) shows these following steps:
- 1)
Select the individuals as parents considering the best objective value.
- 2)
Crossover the parents to form the next generation.
- 3)
Add some random changes to the population (Mutation).
Sequential quadratic programming (SQP) is one of the most effective methods for nonlinearly constrained optimization. It generates steps by solving quadratic subproblems. It uses the derivative of objective and constraint functions so it reaches the global optimum faster. The steps of SQP are shown in Fig.3(b). This approach can be used both in line search and trust-region frameworks, and is appropriate for small or large problems. SQP methods show their strength in solving problems having nonlinear constraints [36].
These two algorithms differ mainly in two points: GA generates population randomly and the best reaches the optimum while SQP generates single point in a deterministic computation and last single point reaches the optimum. To compare the results of the different algorithms will help to understand when to use which algorithm.
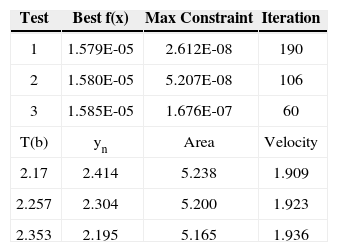
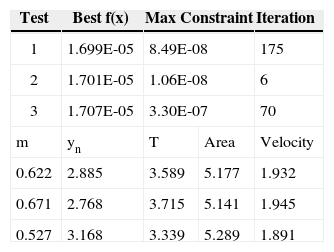
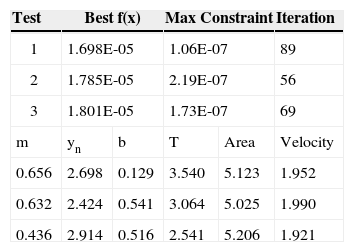
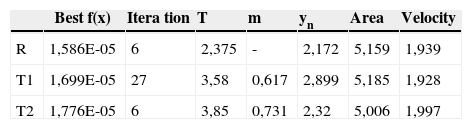
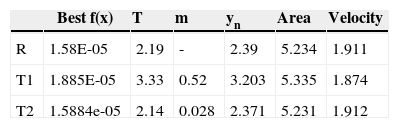
5ResultsMinimum seepage losses of the rectangular, triangular and trapezoidal canal sections are calculated by using both algorithms and results are given in the tables 2, 3 and 4 respectively for GA and in the table 5 for SQP algorithm. Results of GA are given as three best results because it finds different results at each time. Optimum sizes of the channels found in literature are given in table 6 to compare.
Results in literature [5] (R:Rectangular, T1:Triangular, T2:Trapezoidal).
| Best f(x) | T | m | yn | Area | Velocity | |
|---|---|---|---|---|---|---|
| R | 1.58E-05 | 2.19 | - | 2.39 | 5.234 | 1.911 |
| T1 | 1.885E-05 | 3.33 | 0.52 | 3.203 | 5.335 | 1.874 |
| T2 | 1.5884e-05 | 2.14 | 0.028 | 2.371 | 5.231 | 1.912 |
As a result, it is seen that rectangular sections have more efficient results where trapezoidal sections have less in comparison to triangular sections as proven before. From GA and SQP algorithms are much faster than previous algorithms. They generally have given better results than previous studies. SQP seems superior when compared with GA since the results are more robust and reliable. Results of GA can change at each run even though it gives reasonable correct results.
6ConclusionsThis study examined the effectiveness of different algorithms in design of minimum water loss canal sections. Design problem are solved for three different cross sections by using two different algorithms. It is shown that an evolutionary algorithm (GA) and gradient based optimization method(SQP) are also giving reliable results. They are also giving reliable results in a quicker time.
These algorithms should be applied the other version of open channel problems (having different geometries such as parabolic sections or considering cost as objective). Also new algorithms could be applied (Ant Colony, Artifical Bee Colony etc.) in future.