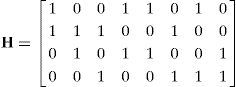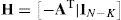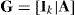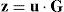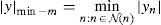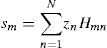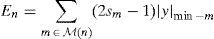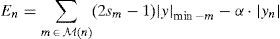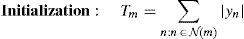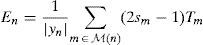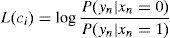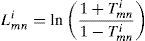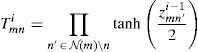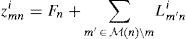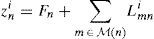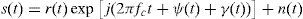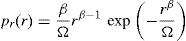The Weibull distribution is a useful statistical model that can be used to describe the multipath fading in nowadays wireless communication environments. In this paper, the bit error rate (BER) performance of Low-Density Parity-Check (LDPC) coded communication systems using different decoding rules is presented over Weibull fading channels by means of comparative computer simulations. It is shown that, especially for the case of the Belief Propagation (BP) decoding rule, significant performance improvement can be achieved in comparison with uncoded transmission when the channel is assumed to have Weibull fading.
Owing to their good performance, Low-Density Parity-Check (LDPC) codes are an important family of error-correction codes employed in current data communication systems (Bastug & Sankur, 2004). They are a type of linear block codes and have been presented by Gallager in the early 1960s (Gallager, 1963). After MacKay and Neal (MacKay, 1999; MacKay & Neal, 1997) have showed that LDPC codes could achieve a Shannon limit error performance similar to that of Turbo codes, LDPC codes have been almost rediscovered in the late 1990s. LDPC codes have several advantages against their biggest rival Turbo codes and these advantages can be summarized as follows: demonstrating better block error performance, error floors in much lower Bit Error Rate (BER) values, the ability to obtain good error performance without the need for interleavers and an iterative-based decoding process instead of a trellis-based one. Another important advantage of LDPC codes is that the complexity of decoding increases linearly with the length of the blocks (Mataracıoğlu and Aygölü, 2008; Lin & Costello, 2004; Richardson & Urbanke, 2001). Currently, LDPC codes have been employed for channel coding on some communication standards such as DVB-S2, WiMAX (802.16e), Wi-Fi (802.11n) and 10Gbit Ethernet (IEEE802.3an). Also, properly designed LDPC codes can exhibit high performance in third-generation (3G) mobile communication systems (Bonello, Chen, & Hanzo 2011; Ohtsuki, 2007; 3GPP, 2005).
The Weibull distribution is a statistical model that has been proposed as an appropriate fading model to describe multipath fading channels for both indoor and outdoor environments. It has been used in numerous wireless communication applications (Babich & Lombardi, 2000; Chen, Liou, & Yu, 2010; Cvetkovic, Djordjevic, & Stefanovic, 2011; Kapucu, Bilim, & Develi, 2013; Singh, Rai, Mohan, & Singh, 2011; Tzeremes & Christodoulou, 2002). Babich et al. have emphasized that the Weibull distribution provides the optimum fit for Digital Enhanced Cordless Telecommunications (DECT) systems operating at 1.89GHz (Babich & Lombardi, 2000). In Tzeremes and Christodoulou (2002) the authors have performed some experiments for a Global System for Mobile Communications (GSM) network, which operates at 900MHz and have proposed that the Weibull distribution can also be used as a fading model for outdoor systems. Furthermore, the Weibull fading model has been recommended for theoretical studies by the IEEE Vehicular Technology Society Committee on Radio Propagation (Adawi et al., 1988). When studies related to the performances of LDPC codes over fading channels are examined it can be seen that, so far, the performance of LDPC codes has been widely investigated over Rayleigh, Rician, Nakagami-m, block fading and non-ergodic block fading channels (Boutros, Fabregas, Biglieri, & Zémor, 2010; Djordjevic, Djordjevic, & Ivanis, 2009; Tan, Li, & Teh, 2011a, 2011b, 2012; Yang, An, & Li, 2011). However, it is important to note that no comprehensive study has been performed on the performance of LDPC codes over Weibull fading channels in the literature. Therefore, the proposed study aims to make a contribution to this topic.
The rest of the paper is organized as follows. Section 2 describes the encoding and decoding processes for LDPC codes. Section 3 describes the structure of the analyzed communication system model with the Weibull fading channel. The simulation results are examined in Section 4 in detail, and finally, conclusions are drawn in Section 5.
2Encoding and decoding processes for LDPC codes2.1Encoding processAn LDPC code is a type of linear block code and is defined by a parity-check matrix H, which contains mostly zeros (0s) and a small number of ones (1s). It is required to set (N−K)×N as the size of the H matrix to obtain an (N, K) LDPC code, where (N−K) is the number of rows, N is the number of columns and K is the number of message bits. The coding rate (R) is defined by R=K/N for an (N, K) LDPC code. When the H matrix is considered, the number of 1 bits in a row is called the row weight (wr) and similarly, the number of 1 bits in a column is called the column weight (wc). LDPC codes can be classified into two categories according to wr and wc as regular and irregular LDPC codes. If the number of 1s in each of the columns and rows is constant, it is called a regular LDPC code, otherwise it is called an irregular LDPC code. A parity-check matrix H for an (8, 4) regular LDPC code with wc=2 and wr=4 is shown in Eq. (1):
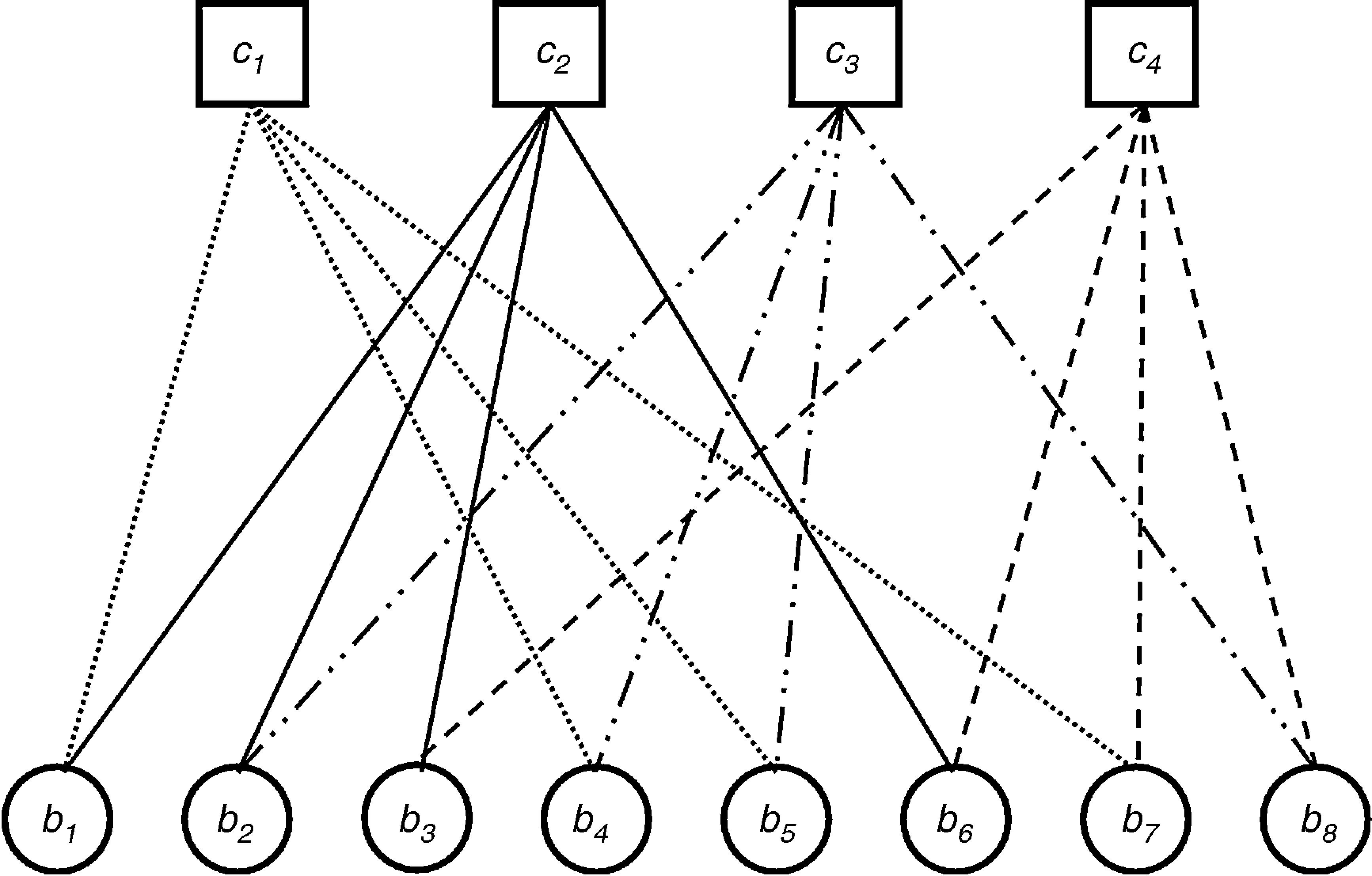
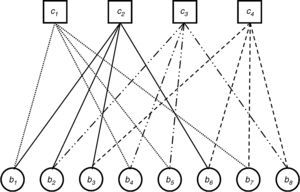
An LDPC code can also be presented by a bipartite graph that was proposed by Tanner in 1981 (Tanner, 1981). Tanner graphs contain N number bit nodes (b1, b2, …, bN), N−K number check nodes (c1, c2,…, cN−K) and several connections between these nodes for an (N, K) LDPC code. The check nodes correspond to the rows of the parity-check matrix H and the bit nodes correspond to the columns of the parity-check matrix H. The connections between the nodes are used for only 1 element of the parity-check matrix H. A Tanner graph for Eq. (1) is shown in Figure 1.
First of all, for the encoding process, it is necessary to create a generator matrix G from the parity-check matrix H. The generator matrix G can be derived by applying the Gaussian elimination method and some matrix operations to the parity-check matrix H. After the Gaussian elimination process, a new parity-check matrix H is obtained as seen in Eq. (2):
where IN−K is a unit matrix with (N−K)×(N−K) size while AT is the transpose matrix of the A matrix. The generator matrix G can be denoted by arranging Eq. (2) as follows:
The last step of the encoding process is multiplying the information bit sequences by the generator matrix G as given below:
where u is the uncoded information sequence with 1×K size and z is the encoded information sequence with 1×N size.2.2Decoding processThe LDPC decoding process can be implemented by using soft or hard decision decoders where the hard decision decoders use the mathematical equations of the Tanner graphs in the decoding procedures. The Bit Flipping (BF) algorithm is generally used in hard decision decoders due to its low complexity. Several studies have been performed to improve the performance of the BF algorithm and modified versions of the BF algorithm, such as the Weighted Bit Flipping (WBF) algorithm, Improved Weighted Bit Flipping (IWBF) algorithm and Implementation-efficient Reliability Ratio based Weighted Bit Flipping (IRRWBF) algorithm, have been derived by researchers (Kou, Lin, & Fossorier, 2001; Lee & Wolf, 2005; Zhang & Fossorier, 2004). Belief Propagation (BP) decoders use the BP algorithm for the decoding steps. The BP algorithm is a soft decoding method that is an efficient and robust technique used in the LDPC decoding procedure.
In the following, it is assumed that Binary Phase Shift Keying (BPSK) modulation is used to explain the LDPC decoding procedures. The BPSK maps a codeword c=(c1, c2,…, cN) into a transmitted sequence x=(x1, x2,…, xN), according to xn=2cn−1 equivalency for n=1, 2,…, N. The received value corresponding to xn after the demodulator is yn=xn+wn, where wn is a random variable with a zero mean and variance of N0/2 (Chen & Fossorier, 2002; Fossorier, Mihaljević, & Imai, 1999; Kou et al., 2001; Liao, Lin, Chang, & Liu, 2007; Ohtsuki, 2007).
2.2.1Weighted Bit Flipping (WBF) algorithmThe performance of the BF decoding algorithm can be improved by including the information on the received symbols in the decoding decision process (Kou et al., 2001). First of all, in the WBF algorithm, m values are computed by the help of Eq. (5) in the WBF algorithm as follows (Kou et al., 2001; Zhang & Fossorier, 2004):
where N(m) = {n: Hmn=1} and m=1, 2, …, M. After the determination of m values, the WBF decoding algorithm is performed according to the steps given below (Kou et al., 2001; Zhang & Fossorier, 2004):Step 1. Syndrome component sm is computed from hard decision sequence z.
Step 2.En is computed using Eq. (7) for n=1, 2, …, N.
Step 3. Flip the bit zn for n=argmax1≤n≤NEn.
If the algorithm reaches the maximum number of iterations or all the parity check equations are satisfied then the algorithm is ended otherwise the algorithm is repeated from Step 1 to Step 3.
2.2.2Improved Weighted Bit Flipping (IWBF) algorithmThe IWBF algorithm is a modified type of the bit nodes information which takes place in the WBF algorithm (Zhang & Fossorier, 2004). The IWBF algorithm determines the reliability of each bit node by using check node and bit node information, in contrast to the WBF algorithm that only takes advantage of the information from check nodes. In the IWBF algorithm a weighting factor (α) is used for the bit message as can be seen from Eq. (9). The weighting factor is a real number and is greater than zero. If α=0 the IWBF algorithm turns into the standard WBF in this case. The steps of the IWBF algorithm can be summarized as follows (Zhang & Fossorier, 2004):
Step 1. Syndrome component sm is computed from hard decision sequence z.
Step 2.En is computed using Eq. (9) for n=1, 2, …, N.
Step 3. Flip the bit zn for n=argmax1≤n≤NEn.
The algorithm repeats from Step 1 to Step 3 until the algorithm reaches the maximum number of iterations or all the parity check equations are satisfied.
2.2.3Improved Weighted Bit Flipping (IWBF) algorithmEven though the reliability ratio based weighted bit flipping algorithm is an efficient hard decision decoding algorithm, it requires a long time for the decoding process. The Implementation-Efficient Reliability Ratio based Weighted Bit Flipping (IRRWBF) algorithm is proposed to solve this time problem in decoding. The IRRWBF algorithm can be divided into four steps: initialization, check node, variable node and decision steps. This algorithm can be summarized as follows (Lee & Wolf, 2005):
Step 1. Syndrome component sm is computed from hard decision sequence z.
Step 2.En is computed using Eq. (12) for n=1, 2, …, N.
Step 3. Flip the bit zn for n=argmax1≤n≤NEn.
In the event that the algorithm reaches the maximum number of iterations or all the parity check equations are satisfied, the algorithm is ended.
2.2.4Belief Propagation (BP) algorithmThe Belief Propagation (BP) algorithm realizes the decoding process as the transfer of information from one node to another node in the Tanner graph. The transferred information means the possibility of there being 1 or 0 bits of information. The BP algorithm is also known as the Message Passing (MP) algorithm in the literature. It is necessary to define some notations associated with a given iteration as follows (Fossorier et al., 1999; Kou et al., 2001; Liao et al., 2007; Ohtsuki, 2007):
Fn: The log-likelihood ratio (LLR) of bit n which is derived from the received value yn.
Lmni: The LLR of the bit n sent from the check node m to the bit node n in the ith iteration.
zmni: The LLR of the bit n sent from the bit node n to the check node m in the ith iteration.
zni: The a posteriori LLR of the bit computed at each iteration.
The BP algorithm can be mathematically described as follows by referring to the parameters given above (Fossorier et al., 1999; Kou et al., 2001; Liao et al., 2007; Ohtsuki, 2007):
Initialization: The a priori probability (L(ci)) is calculated by the decoder in this step using the following equation:
Step 1. In the first step, Lmni is updated for each m, n as follows:
whereStep 2. In the second step, zmni and zni are updated for each m, n as follows:
Decision: For stopping criteria, it is first of all necessary to create a vector such as xˆi=xˆni, where xˆni=1 if zni>0 and xˆni=0 if zni<0.
- a.
If HxˆiT=0, the decoding algorithm stops and xˆi is considered as a valid decoding result, otherwise the algorithm is repeated from Step 1.
- b.
If the algorithm reaches the maximum number of iterations, the algorithm is ended.
The Weibull distribution is a statistical model and has been proposed as an appropriate fading model to describe multipath fading for both indoor and outdoor environments. The Weibull distribution is used in many wireless communication and image processing applications (Babich & Lombardi, 2000; Chen et al., 2010; Cvetkovic et al., 2011; Kapucu et al., 2013; Singh, Rai, Mohan, & Singh, 2011; Tzeremes & Christodoulou, 2002). When a Weibull fading channel is considered, the received signal s(t) can be defined as follows (Cvetkovic et al., 2011):
where fc is the carrier frequency, ψ(t) is the information bearing phase, γ(t) is the random phase uniformly distributed in [0,2π), r(t) is the Weibull distributed random variable with the probability density function (PDF) and n(t) is the AWGN noise that is a random variable with a zero mean and variance N0/2. The PDF of the Weibull distribution can be defined aswhere Ω=Erβ (E⋅ represents the expected value operator), Ω is also known as the scaling parameter, and β is the Weibull fading parameter with values 0<β<∞. As a special case, if β=1, the Weibull distribution turns into an exponential distribution and if β=2 the Weibull distribution turns into a Rayleigh distribution in this case (Chen et al., 2010; Cvetkovic et al., 2011).
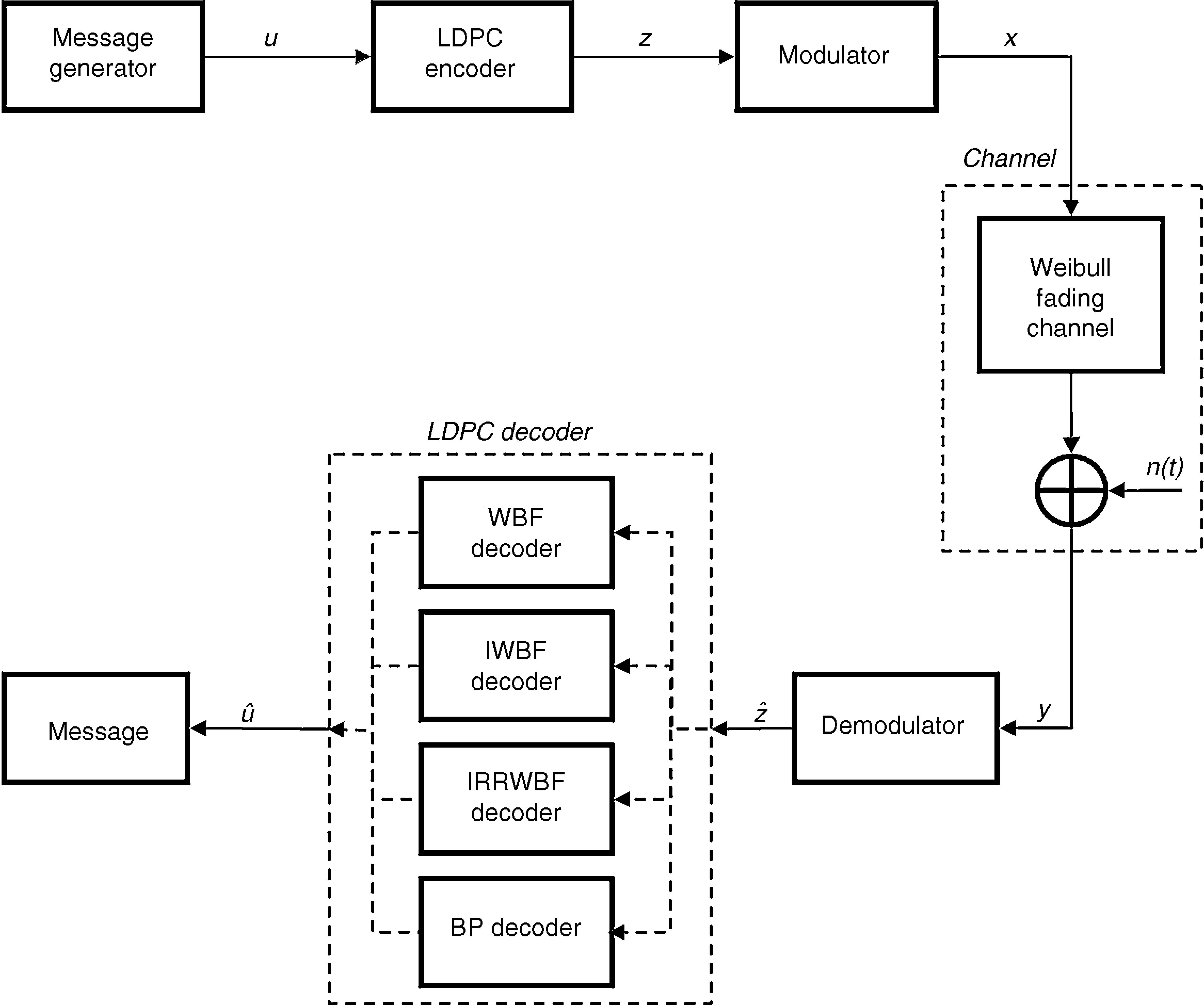
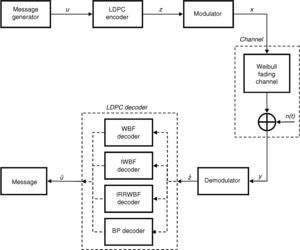
The LDPC coded communication system model is shown in Figure 2. The simulation processes are performed for a regular LDPC code, which has (1008, 504) block length and ½ code rate. The message generator block is shown in the first part of Figure 2 and generates random binary data as message information. The output sequence of the message generator block (u) consists of 0 and 1 bits of the message with 1×K length. The LDPC encoder block performs the channel coding for message bits so that resulting bits gain robustness and are less changed by various effects such as noise and interference originating from disruptive factors while they pass through the channel.
The LDPC encoder block encodes the input message information (u) with 1×K length using the procedures described in Section 2.1 and produces a 1×N length z sequence in the LDPC encoder block output. The modulator block carries out the modulation process for the z sequence according to BPSK modulation type. The modulated and LDPC coded message bits are stored in the output of the modulator block named x. After the modulation and channel coding processes, message bits are applied to the communication channel which is composed of a Weibull fading channel and AWGN noise. The message information from the output of the channel is shown by the y sequence and is applied as input to the demodulator block, as seen in Figure 2. The demodulator block performs the demodulation process for the input y sequence and produces a zˆ sequence with 1×N length. The LDPC decoder block performs the decoding process according to WBF, IWBF, IRRWBF or BP decoder. A uˆ sequence with 1×K length is obtained from the output of the LDPC decoder block after the decoding process. The BER performance of the analyzed system is obtained by comparing input sequence u with output sequence uˆ.
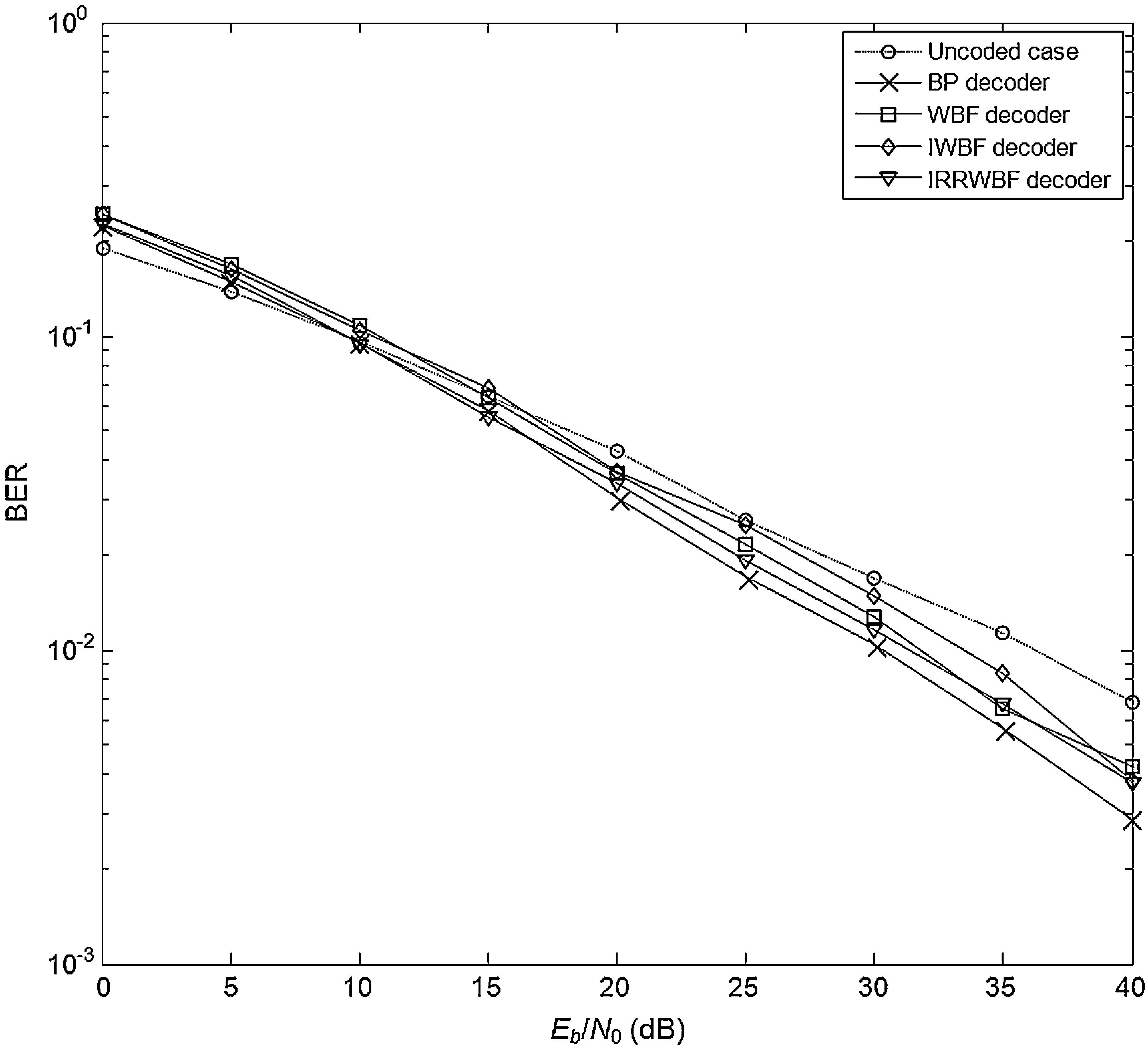
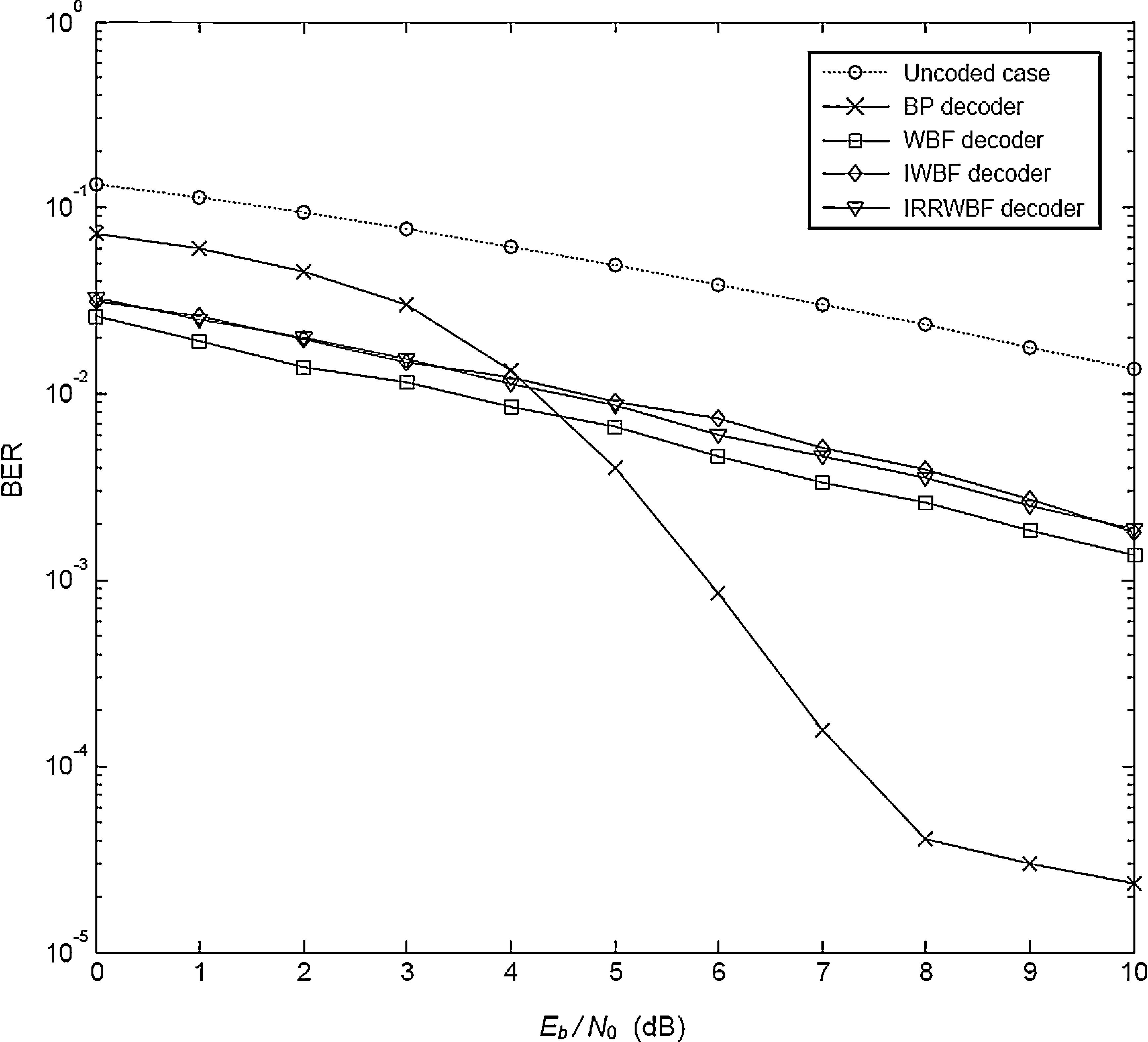
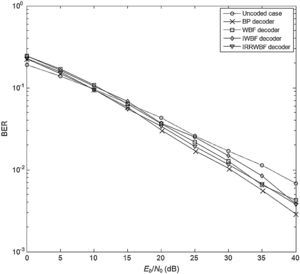
4Comparative performance analysisThe BER performances of LDPC coded communication systems are evaluated by Monte-Carlo simulations, and the number of Monte-Carlo trials was set to 1000. The BER performance results of the system with (1008, 504) LDPC code are shown in Figures 3–5 where the simulations are performed for 25 iterations in each LDPC decoder employed. In all figures, the effect of the Weibull channel is incorporated into the simulation by varying the value of β while the Ω is set to 1 in each condition. Figure 3 illustrates the BER performance of the system that runs in a Weibull fading channel. In this simulation, the fading parameter (β) is set to 1. It is evident from the figure that the BER performances of WBF, IWBF and IRRWBF are observed close to each other, while the BP decoder outperforms the other hard decision decoders, and the BER performance of this decoding rule is up to 6.5dB better than that of the uncoded case at a BER level of 10−2.
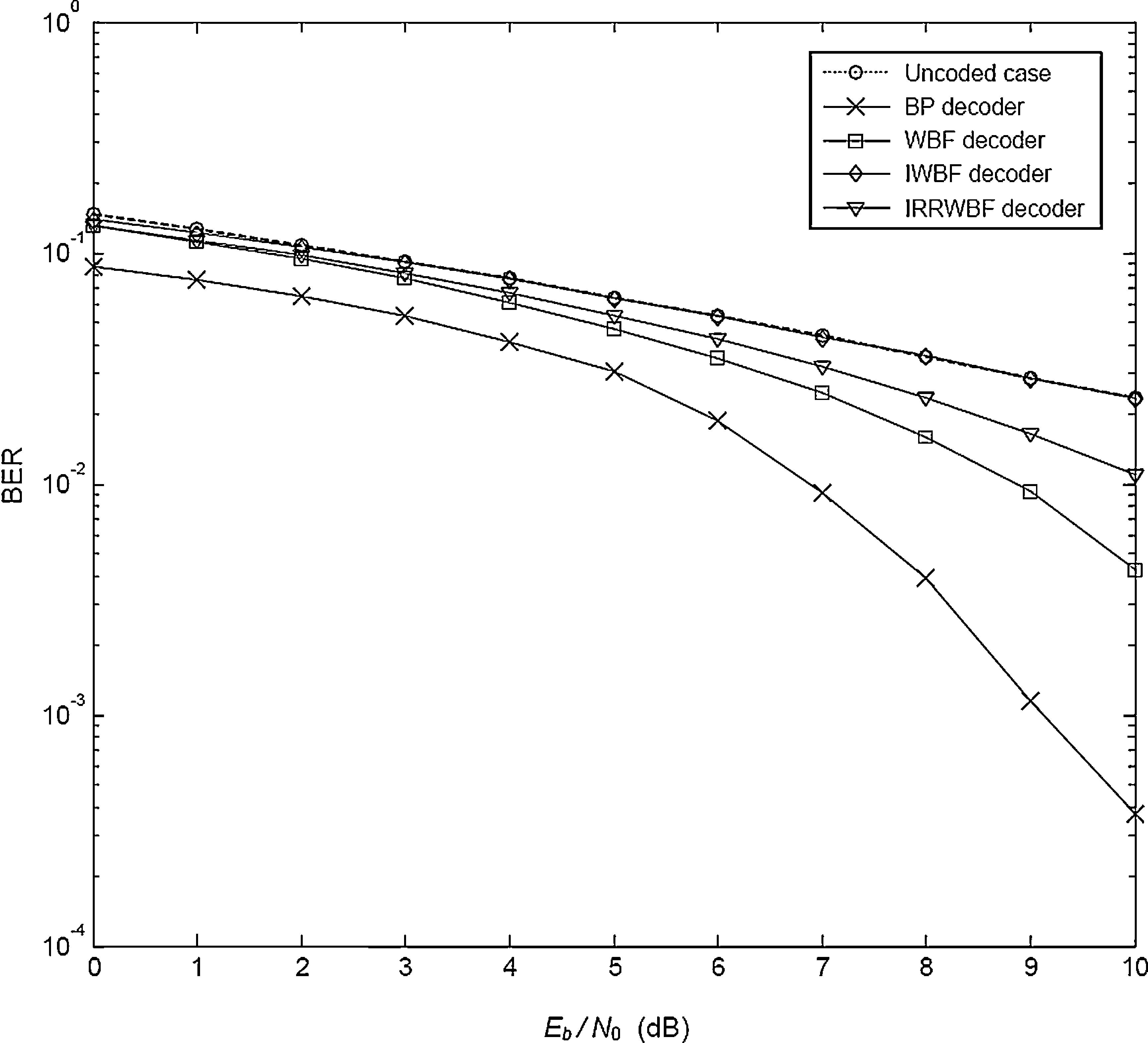
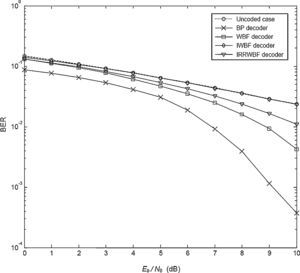
Figure 4 depicts the performance of the system when the Weibull fading parameter (β) is increased to 2. Even though the hard decision decoders give better results according to the previous analysis, these decoders still cannot provide as good performance as that obtained in the BP decoder. As can be seen, the BER performance of the BP decoder is always better than that of the other decoders. Also note that the IWBF decoder presents the worst BER values even though its performance is almost the same as that of the uncoded case. When compared with the uncoded case, the improvement achieved by the BP decoder is nearly 2.5dB for BER of 10−1.
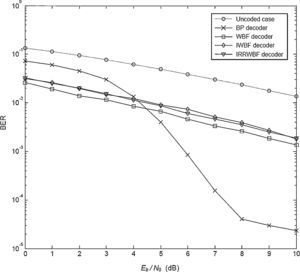
The final analysis is performed by setting β to 2.5 for the same system. The performance curves are seen in Figure 5. Although the BP decoder cannot give a satisfactory performance as well as the hard decision decoders until 4.5dB, this detector outperforms the other three types decoders for Eb/N0 values greater than 4.5dB.
Comparison between the performance for the uncoded case and the BP decoding performance reveals that the improvement achieved by the BP decoder is nearly 7dB at a BER level of 10−2.
5ConclusionsThe Weibull distribution has been employed as an appropriate fading model in the literature for theoretical channel definition. In this study, the BER performance of LDPC codes in Weibull fading channels was analyzed for different decoding rules by means of comparative computer simulations. An LDPC coded BPSK communication system was designed as a communication infrastructure to perform the analysis. Four different decoding rules and a regular LDPC code with (1008, 504) block length and ½ code rate were used in simulations. From all the simulation studies realized in a Weibull fading channel, we can see that significant performance improvement can be obtained in comparison with the uncoded transmission especially when the BP decoding rule is employed in the receiver.
Conflict of interestThe authors have no conflicts of interest to declare.
This work was supported by the Research Fund of Erciyes University, grant number: FBD-10-3092. The authors thank to Proofreading & Editing Office of Erciyes University for careful reading and corrections on the manuscript.
Peer review under the responsibility of Universidad Nacional Autónoma de México.