Background/Objective: The Padua Inventory-Revised (PI-R) is a widely applied instrument to measure obsessive-compulsive symptoms in clinical and nonclinical samples. We conducted a reliability generalization meta-analysis on the PI-R. Method: An exhaustive literature search yielded 118 empirical studies that had applied the PI-R, from which 30 studies (33 samples) reported an original reliability estimate. Results: Assuming a random-effects model, the average internal consistency reliability (Cronbach's alpha) was .92 (95% CI [.91, .93]) for the total scores, and ranged from .74 to .89 for the subscales. Assuming mixed-effects models, moderator analyses showed a positive statistically significant association between the standard deviation of the total scores and the reliability coefficients (p = .002; R2 = .38). Conclusions: In terms of reliability, the PI-R scale was found to be adequate for both research and clinical purposes, although exhibiting large heterogeneity across studies. Future empirical studies using the PI-R should be required to provide at least one reliability estimate based on their own data.
Antecedentes/Objetivo: El Padua Inventory-Revised (PI-R) es un instrumento ampliamente utilizado para medir los síntomas obsesivo-compulsivos en muestras clínicas y no clínicas. Llevamos a cabo un meta-análisis de generalización de la fiabilidad del PI-R. Método: Una búsqueda exhaustiva de la literatura arrojó 118 estudios empíricos que habían aplicado el PI-R, de los cuales 30 estudios (33 muestras) reportaron una estimación propia de la fiabilidad. Resultados: Asumiendo un modelo de efectos aleatorios, la fiabilidad en términos de consistencia interna promedio (alfa de Cronbach) fue de 0,92 (IC del 95% [0,91, 0,93]) para las puntuaciones totales, y osciló entre 0,74 y 0,89 para las subescalas. Asumiendo modelos de efectos mixtos, los análisis de moderadores mostraron una relación positiva estadísticamente significativa entre la desviación típica de las puntuaciones totales y los coeficientes de fiabilidad (p = 0,002; R2 = 0,38). Conclusiones: En términos de fiabilidad, se encontró que el PI-R es adecuado tanto para fines clínicos como de investigación, aunque con una alta heterogeneidad entre los estudios. Es necesario que los estudios empíricos futuros que apliquen el PI-R proporcionen al menos una estimación de la fiabilidad basada en sus propios datos.
Obsessive-compulsive disorder (OCD) is a mental disease characterized by the presence of obsessions and/or compulsions that interfere with everyday life (5th ed. [DSM-5]; American Psychiatric Association, 2013). On the one hand, obsessions are recurrent and persistent ideas, images or impulses that the person considers unpleasant, causing marked anxiety or distress. On the other hand, compulsions are repetitive behaviours or mental acts that seek to reduce the distress caused by obsessions. The prevalence of OCD around the world ranges from 0.9% to 1.8%, with females being more affected than males in adulthood, although OCD is more common in boys than in girls in childhood (Brakoulias et al., 2018; Kiverstein et al., 2019; Osland et al., 2018; Remmerswaal et al., 2020; Rosa-Alcázar et al., 2021).
Sanavio (1988) developed the Padua Inventory (PI), a self-report instrument widely applied to assess obsessive-compulsive symptoms in adults, and used for diagnosis and screening of OCD in both clinical and research settings. The original PI consists of 60 items describing common obsessional and compulsive behaviour, and each item is rated on a 5-point scale from 0 (not at all) to 4 (very much), so that higher scores indicate greater disturbance associated with OCD symptoms.
Two shorter versions of the original PI have also been widely extended and applied in the assessment of OCD symptomatology: The Padua Inventory-Revised (PI-R; van Oppen et al., 1995), and the Padua Inventory-Washington State University Revision (PI-WSUR; Burns et al., 1996). The PI-R comprises 41 items grouped in five subscales after removing 19 items from the original PI, whereas the PI-WSUR consists of 39 items also organized into five subscales after deleting 21 items from the original PI. The present paper focused on the analysis of the reliability of the PI-R across different samples of participants and application contexts.
Van Oppen et al. (1995) developed the PI-R after noting that the four-factor structure of the original PI was suitable for the general population, but not so much for OCD patients. They administered the PI to three samples including OCD patients, anxious patients and normal subjects, respectively, and found a five-factor solution with an adequate fit to the data from the three samples. Next, they eliminated the PI items that did not fit into one of the five factors, and finally proposed the new PI-R with 41 items grouped as follows: impulses (7 items), washing (10 items), checking (7 items), rumination (11 items), and precision (6 items). The internal consistency reliability for the PI-R total scale was .89 in the OCD patients (subscales ranged from .77 to .93), .92 in the anxious patients (subscales ranged from .65 to .89), and .92 in the normal subjects (subscales ranged from .66 to .87).
The PI-R was originally developed in Dutch language and later adapted to several languages and cultures, including English, Turkish and German. Beşiroğlu et al. (2005) applied a Turkish version of the scale to five samples of OCD patients, anxious patients, depressed patients, healthy adults, and undergraduate students. They essentially identified the same five factors as the original PI-R (although the 6 items in the precision subscale loaded on two different factors), found a coefficient alpha of .95 for the total scale in the entire sample (subscales ranged from .79 to .92) and a test-retest coefficient of .91 (subscales ranged from .81 to .90). Gönner et al. (2010) validated a German version of the PI-R in an OCD sample, but their data did not support the five factor structure from the original PI-R. For total scores, the coefficient alpha was .93 and ranged from .82 to .96 in the five subscales of the original test.
Our main objective in this study was to analyse the reliability of the PI-R across its numerous applications in empirical studies. Psychometric theory states that reliability is not an inherent property of the test, but rather of the scores obtained in each application of the test (Irwing et al., 2018). Thus, the reliability of a given test can change from one application to another, depending on the composition and variability of the samples. As reliability usually varies in each test administration, researchers should report the reliability obtained with their own data. However, it is a common malpractice that researchers induce the reliability from previous applications of the test instead of reporting original estimates with the data at hand (Shields & Caruso, 2004). For instance, researchers might report the reliability estimate from previous validation studies of the test (reliability induction by precise report), mention that previous studies show that the test has a good reliability without providing specific values (reliability induction by vague report), or even omit any reference to test scores reliability (reliability induction by omission).
Meta-analysis allows researchers to statistically integrate multiple reliability coefficients resulting from applying a given test to different samples and contexts. Vacha-Haase (1998) coined the term reliability generalization (RG) to refer to this kind of meta-analysis. The purpose of an RG meta-analysis is to estimate the average reliability of the test scores, analyse the variability of the reliability coefficients and, where appropriate, look for moderator variables that account for at least part of this variance (Sánchez-Meca et al., 2013).
Several RG meta-analyses focused on some of the most relevant instruments for measuring OCD symptomatology have been conducted in recent years. Sánchez-Meca et al. (2017) performed an RG meta-analysis on the original Sanavio's (1988) Padua Inventory (PI), finding average internal consistency and test-retest reliability of .94 and .84, respectively. There is also an RG meta-analysis carried out by Rubio-Aparicio, Núñez-Núñez et al. (2020) on the PI-WSUR version (Burns et al., 1996) of the PI, with averages of .93 and .77 for coefficient alpha and test-retest reliability, respectively. However, out of the three versions of the Padua Inventory, original PI, PI-WSUR, and PI-R; the latter is the only version without a published RG meta-analysis. In this paper we report the first RG meta-analysis focused on the PI-R version (van Oppen et al., 1995).
Reliability is one of the most important properties of a test scores. Ascertaining whether reliability changes from one application to the next is an important question that must be empirically investigated. The PI-R, together with the PI-WSUR, is one of the two shortened versions of the original PI, but the comparability with the other versions in terms of reliability remains unknown to date. With the purpose of examining the reliability of the PI-R scores, we conducted an RG meta-analysis of the empirical studies that applied the Padua Inventory-Revised (PI-R; van Oppen et al., 1995). In particular, we aimed to: (a) estimate the average reliability of test scores obtained in the studies that reported reliability estimates of the PI-R with the data at hand; (b) examine the variability among the reliability estimates; (c) search for characteristics of the studies that can be statistically associated to the test score reliability coefficients; (d) estimate the reliability induction rates of the PI-R; and (e) investigate the generalizability of the results of our RG meta-analysis by comparing the sample characteristics of the studies that induced reliability with those that estimated score reliability with the own data.
MethodThis RG study was reported following the Guidelines for conducting and reporting reliability generalization meta-analyses (REGEMA; Sánchez-Meca et al., 2021). Appendix A includes the REGEMA checklist for the present meta-analysis.
Selection criteria of the studiesTo be included in the meta-analysis, each study had to fulfil the following criteria: (a) to be an empirical study where the PI-R, or an adaptation maintaining the 41 items, was applied to a sample of at least 10 participants; (b) to report any reliability estimate based on the study-specific sample; (c) the paper had to be written in English; (d) samples of participants from any target population were accepted (community, clinical, or subclinical populations); and (e) the paper might be published or unpublished. The following exclusion criteria were applied: (a) N = 1 or case series, and (b) studies that applied the Sanavio´s (1988) original version of the Padua Inventory, the PI-WSUR (Burns et al., 1996), or any other version that did not maintain the 41 items structure of the PI-R.
Searching for the studiesAlthough the PI-R was published in 1995, it was adapted from the Sanavio´s original version of the Padua Inventory from 1988, so that the search period of relevant studies covered from 1988 to June 2020 inclusive. The following databases were consulted: PROQUEST (full list of databases), PUBMED, and Google Scholar. In the electronic searches, the keywords “Padua Inventory” were used to be found in the full text of the documents. Furthermore, the references of the studies retrieved were also checked in order to identify additional studies that might fulfil the selection criteria.
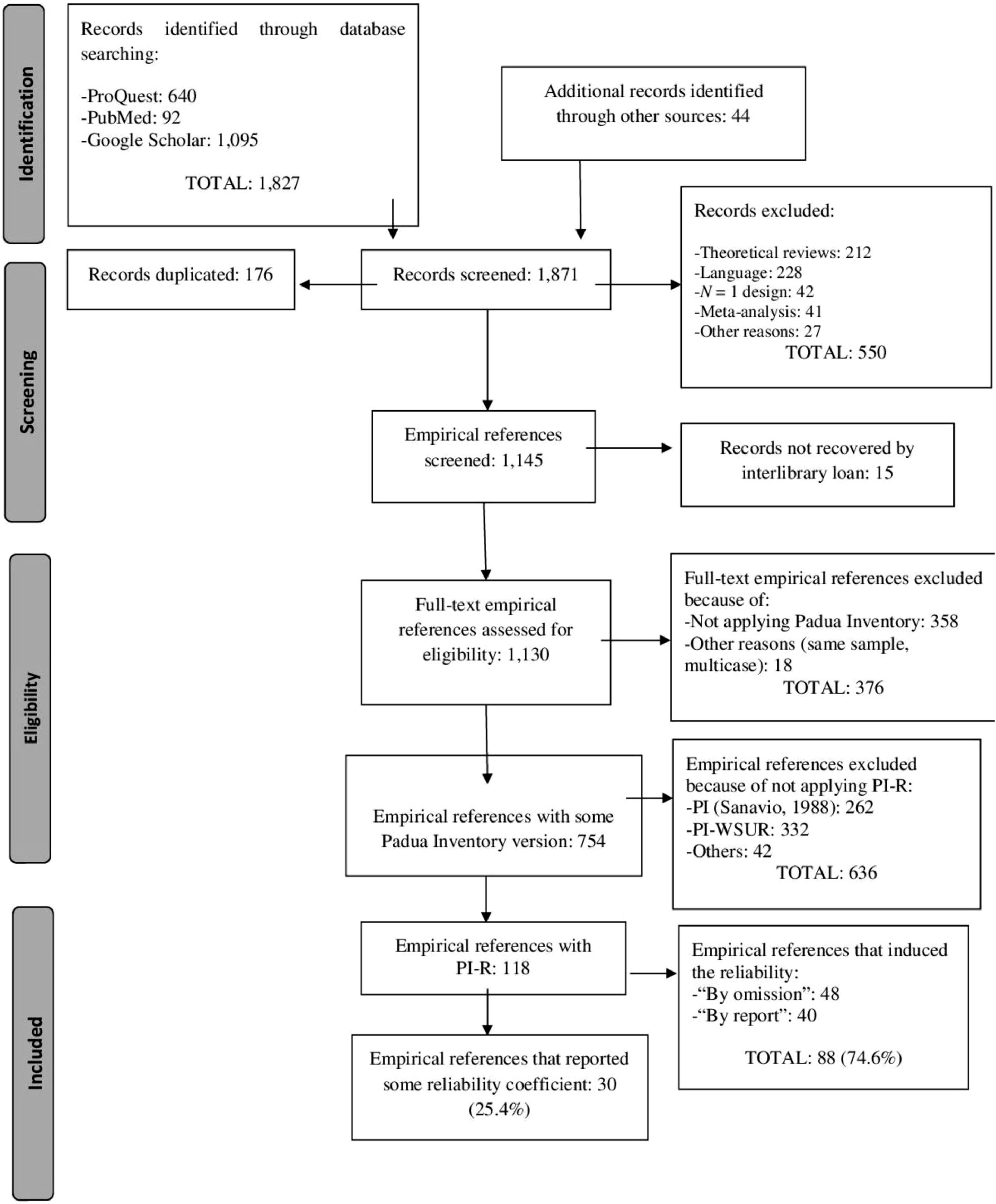
Figure 1 displays a flowchart describing the selection process of the studies. The search yielded a total of 1,871 references, out of which 1,753 were removed for different reasons. The remaining 118 references were empirical studies that had applied the PI-R. Out of them, 30 (25.4%) reported some reliability estimate with the data at hand, whereas the remaining 88 studies (74.6%) induced the reliability of the PI-R from previous applications of the test.
Data extractionTo explore how study characteristics can affect score reliability of the PI-R, the following moderator variables were coded: (a) mean and standard deviation (SD) of the total scores of the PI-R as well as of each of the five subscales; (b) mean of the participants’ age (in years); (c) gender distribution of the sample (% male); (d) sample ethnicity (% Caucasian); (e) mean and SD of the history of the disorder (in years, for clinical samples only); (f) target population; (g) percentage of clinical participants in the sample; (h) type of clinical disorder; (i) geographical location of the study; (j) test version; (k) administration format; (l) study focus; (m) focus of the psychometric study; (n) sample size; (o) time interval (in weeks) for test-retest reliability; and (p) year of the study. Alongside these moderator variables, alpha and test-retest coefficients were extracted for the total scale and for the subscales where reported.
The protocol for extracting the study characteristics was applied not only to studies that reported reliability, but also to those that induced it. This comparison is critical to determine the extent to which the results of an RG meta-analysis (based only on studies that reported reliability) can be generalized to all studies that applied the test of interest, regardless of whether or not they reported reliability.
To examine the reliability of the coding process, all studies that had applied the PI-R (118 studies, 166 independent samples) were doubly coded by two independent raters, both psychologists with a PhD in psychology and specialized in meta-analysis. The results were highly satisfactory overall, with kappa coefficients ranging between .96 and 1.0 (M = .99) for categorical characteristics, and intraclass correlations between .99 and 1.0 (M = .99) for continuous variables. Inconsistencies between raters were resolved by consensus.
Reliability estimatesIn this meta-analysis, two types of reliability coefficients were taken into account: alpha coefficients to assess internal consistency of the measures, and Pearson correlation coefficients to estimate test-retest temporal stability. These two types of reliability coefficients were extracted for the PI-R total score and for each one of the five subscales. Two alternative forms of alpha coefficients were considered in the meta-analysis, namely untransformed coefficients and transformed ones using the formula proposed by Bonett (2002). Pearson correlation coefficients, r, were transformed using Fisher´s Z formula. These transformations were applied in order to normalize the distribution of the coefficients and to stabilize their variances.
Statistical analysisSeparate meta-analyses were conducted for alpha coefficients and for test-retest coefficients. Furthermore, separate meta-analyses were conducted for the reliability coefficients obtained from the total scale and for each of the five subscales. To obtain summary statistics of reliability coefficients in each meta-analysis, a random-effects model was assumed (Cooper et al., 2019). This implied that the reliability coefficients were weighted by inverse variances. The between-studies variance was estimated by restricted maximum likelihood (Langan et al., 2019). The 95% confidence interval around each overall reliability estimate was computed with the improved method proposed by Hartung and Knapp (2001). To facilitate result interpretation, the average reliability coefficients and their confidence limits obtained with Bonett´s or Fisher´s Z transformations, were back-transformed into the original metrics.
Heterogeneity among reliability coefficients was examined by constructing a forest plot and by calculating the Q test, the I2 index, and the between-study standard deviation. Moreover, a 95% prediction interval (PI) was calculated around the pooled reliability estimate, in order to determine the range of expected reliability coefficients in future primary studies (IntHout et al., 2016). For alpha coefficients of the total scale, we also used Egger's test and constructed a funnel plot with the trim and‐fill method to analyze the risk of publication bias (Duval & Tweedie, 2000).
For meta-analyses with at least 20 coefficients where evidence of heterogeneity was found, moderator analyses were performed through weighted ANOVAs and meta-regression analyses for categorical and continuous variables, respectively. Mixed-effects models were assumed, using the improved method proposed by Knapp and Hartung to test for moderators (Gonzalez-Mulé & Aguinis, 2017; Rubio-Aparicio, López-López et al., 2020; Rubio-Aparicio et al., 2017; Tipton et al., 2019). Additionally, a predictive model included the most relevant study characteristics. All statistical analyses were carried out with the metafor package in R.
ResultsMean reliability and heterogeneityAppendix B presents the references of the 31 studies that reported at least one reliability estimate with the data at hand1. Of the 31 studies, two of them (De Bruin, Rassin, & Muris, 2005; McFarlane et al., 2015) reported the reliability in a form not suitable for inclusion in the RG meta-analysis (e.g., reporting of reliability coefficients as a range). The remaining 29 studies were included in our RG study. Several studies reported reliability coefficients for two or more different samples, so that the database of our RG study included a total of 33 independent samples2. From these, 31 alpha coefficients and only two test-retest coefficients were calculated.
All studies were written in English. The total sample size was N = 10,170 participants (min. = 13, max. = 2,976), with mean = 308 participants per sample (M = 190; SD = 526). Regarding the location of the studies, three continents were represented: Europe with 23 samples (69.7%), Asia with 6 samples (18.2%), and North America with 4 samples (12.1%). All the Asian studies were conducted in Turkey.
Although the statistical analyses were performed both using the untransformed alpha coefficients and Bonett´s transformation, the results were very similar. Thus, results are presented only for transformed alpha coefficients, back-transforming the means and their respective confidence limits into the original metric.
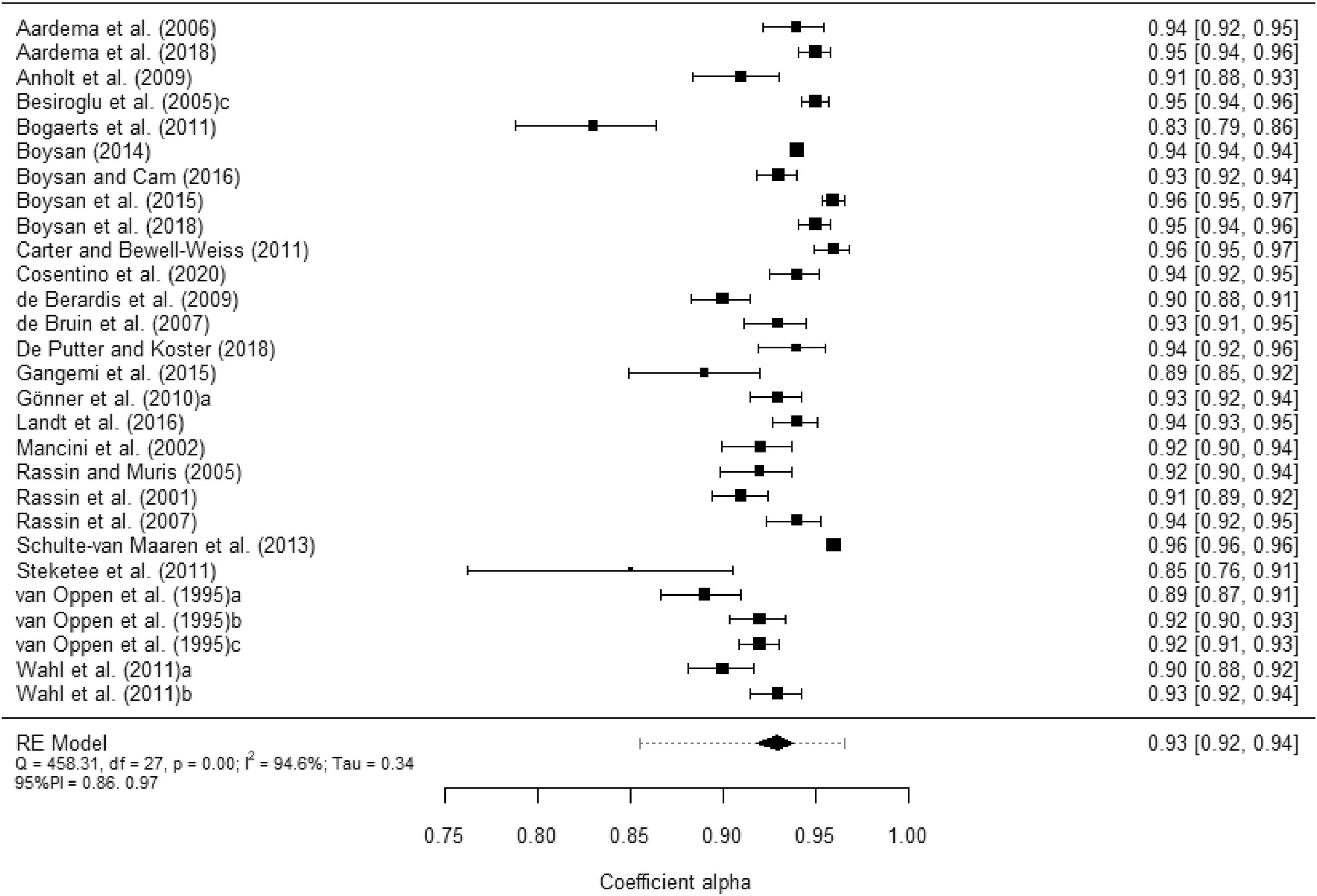
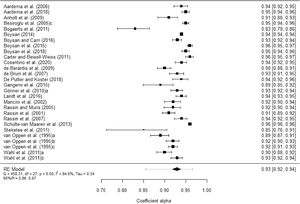
Table 1 presents the main summary statistics for the alpha coefficients obtained from the total scores and from each subscale. Figure 2 displays a forest plot of alpha coefficients for the PI-R total scores in each study. In addition, Appendix C contains the forest plots of alpha coefficients for each subscale scores. The 28 estimates reported for the total scale yielded a mean coefficient alpha of .92. Subscales exhibited lower mean reliability coefficients, with Washing yielding the largest estimates (M = .89), followed by Checking (M = .88) and Rumination (M = .87). Impulses (M = .79) and Precision (M = .74) were the subscales with the poorest average reliabilities. Large I2 indices were found (> 90%), both for the total score and for the subscales. In addition, the 95% prediction intervals were very wide, indicating large uncertainty regarding the expected reliability in future primary studies applying the PI-R. As a consequence, moderator analyses were in order.
Mean alpha coefficients, 95% confidence and prediction intervals, and heterogeneity statistics for the PI-R total scores and the five subscales.
| Total Scale/Subscale | k | α+ | 95% CI | 95% PI | Q | I2 | ||
|---|---|---|---|---|---|---|---|---|
| LL | UL | LL | UL | |||||
| Total scale | 28 | .92 | .91 | .93 | .85 | .96 | 458.306 ⁎⁎⁎ | 94.6 |
| Impulses | 19 | .79 | .76 | .82 | .65 | .87 | 176.122 ⁎⁎⁎ | 90.6 |
| Washing | 20 | .89 | .86 | .91 | .68 | .96 | 777.177 ⁎⁎⁎ | 97.6 |
| Checking | 18 | .88 | .86 | .89 | .80 | .93 | 175.537 ⁎⁎⁎ | 91.4 |
| Rumination | 19 | .87 | .85 | .89 | .75 | .93 | 313.529 ⁎⁎⁎ | 94.6 |
| Precision | 18 | .74 | .69 | .77 | .49 | .86 | 224.948 ⁎⁎⁎ | 94.0 |
Notes. k = number of studies. α+ = mean coefficient alpha. CI = confidence interval. PI = prediction interval. LL and UL: lower and upper limits of the 95% confidence and prediction intervals for α+. Q = Cochran's heterogeneity Q statistic; with k – 1 degrees of freedom. I2 = heterogeneity index.
Forest plot displaying the alpha coefficients (and 95% confidence intervals) for the PI-R total scores. The outer edges of the bottom polygon indicate the confidence interval limits and the dotted line indicates the bounds of the 95% prediction interval. Tau = between-study standard deviation.
Regarding test-retest reliability, only two samples reported this kind of reliability for the total scores with a mean of .90 (95%CI: .87 to .93).
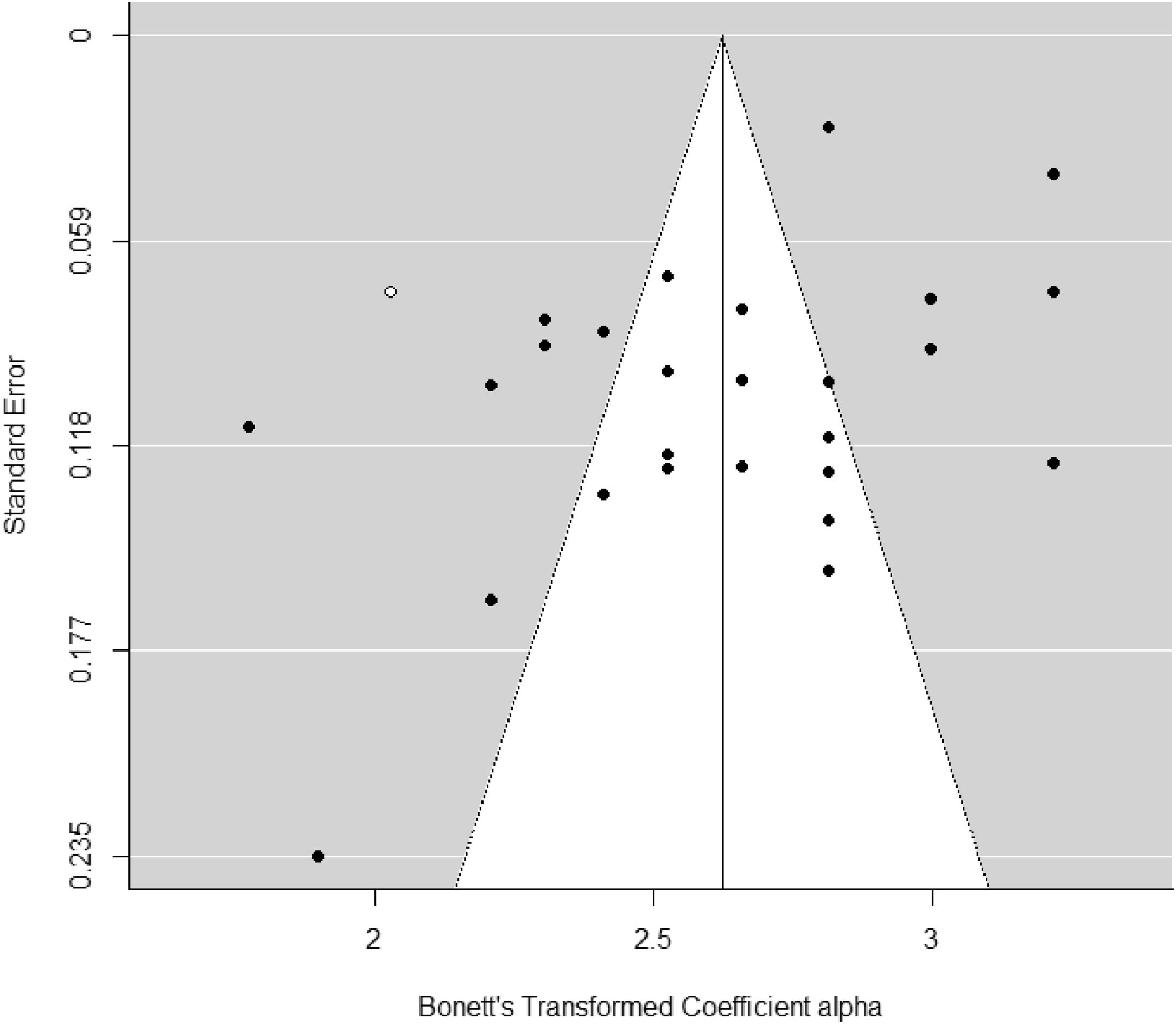
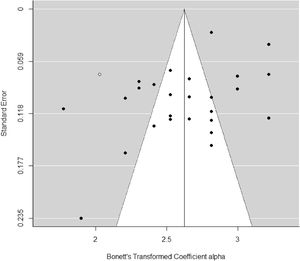
Publication bias for alpha coefficients of the total PI-R scale was assessed through funnel plot applying Egger's test and the trim-and-fill method. Egger's test yielded a statistically significant result for the interception (p = .028), suggesting some evidence of funnel plot asymmetry. Furthermore, the trim-and-fill method imputed one additional reliability estimate to achieve symmetry of the funnel plot (see Figure 3). When a mean coefficient alpha was calculated using the 28 reliability estimates plus the imputed value, the mean coefficient alpha was of .92. If we compare the new effect with that obtained using the 28 original reliability estimates (∝+= .929), the difference is negligible.
Analysis of moderator variablesDue to the small number of studies reporting reliability estimates for the subscales (20 studies or less), the analysis of moderators was conducted only for the alpha coefficients based on the total scores.
Table 2 presents the results of simple meta-regressions models. Out of the different moderators analysed, only the standard deviation of test scores exhibited a statistically significant relationship with alpha coefficients (p = .002) and with a 38% of variance accounted for. In particular, this predictor exhibited a positive relationship with alpha coefficients, so that larger reliability estimates were obtained as the standard deviation of the test scores increased.
Results of simple meta-regression models applied on alpha coefficients for the total scores, taking continuous moderator variables as predictors.
| Predictor variable | k | bj | F | p | QE | R2 |
|---|---|---|---|---|---|---|
| Mean Total scores | 26 | 0.0031 | 0.55 | .464 | 434.528⁎⁎⁎ | .0 |
| SD of Total scores | 26 | 0.0344 | 12.42 | .002 | 209.838⁎⁎⁎ | .38 |
| Mean age (years) | 28 | -0.0065 | 0.55 | .464 | 454.743⁎⁎⁎ | 0.0 |
| Gender (% male) | 26 | -0.0009 | 1.56 | .223 | 331.585⁎⁎⁎ | .03 |
| % of clinical sample | 28 | -0.0004 | 0.05 | .822 | 455.702⁎⁎⁎ | 0.0 |
| Year of the study | 28 | 0.0176 | 3.56 | .070 | 361.529⁎⁎⁎ | .11 |
Notes. k = number of studies. bj = slope estimate. F = Knapp-Hartung's statistic for testing the significance of the predictor (the degrees of freedom for this statistic are 1 for the numerator and k – 2 for the denominator). p = probability level for the F statistic. QE = statistic for testing the model misspecification. R2 = proportion of variance accounted for by the predictor.
Table 3 shows the results of the ANOVA models incorporating categorical moderator variables. A 17% of variance accounted for continent was found, although no statistically significant differences were found when grouping alpha coefficient by this variable (p = .068).
Results of the weighted ANOVAs applied on alpha coefficients for the total scores, taking categorical variables as moderators.
Notes. k = number of studies. α+ = mean coefficient alpha. LL and LU = lower and upper 95% confidence limits for α+. F = Knapp-Hartung's statistic for testing the significance of the moderator variable. QW = statistic for testing the model misspecification. R2 = proportion of variance accounted for by the moderator.
Out of the different mixed-effects models presented in Tables 2 and 3, indicators of statistical significance (e.g., low p-value) and predictive power (e.g., high R2 estimate) suggest that the most useful model to predict the reliability of PI-R scores is that including the SD of the total scores. We examined goodness-of-fit indices, namely the Akaike and Bayesian Information Criteria, and obtained values of AIC = 17.64 and BIC = 21.17 for the model with score SD as the only moderator. We also examined multiple mixed-effects meta-regression models with publication year and/or continent in addition to score SD, but the AIC and BIC indices did not support this additional complexity. Thus, the simple meta-regression model including the SD of the total scores can be used to estimate an expected coefficient alpha with the following predictive model: α′=1−e−(1.833+0.034*SD).
Estimating reliability inductionAs Figure 1 presents, out of the 118 studies that applied the PI-R, 88 induced reliability, which implies a 74.6% of reliability induction for this test. Out of these 88 studies, 48 (54.5%) failed to make any references to the reliability of PI-R scores (reliability induction by omission), whereas the remaining 40 studies (45.5%) did mention reliability but failed to report any original estimates. In particular, 23 studies (26.1%) mentioned reliability without reporting any specific values (reliability induction by vague report), whereas 17 studies (19.3%) reported reliability estimates from previous studies (reliability induction by precise report).
Comparing studies inducing and reporting reliabilityRG meta-analyses aim to generalize results to the population of studies that have applied the test, regardless of whether they reported or induced reliability. The validity of such generalization will depend on how similar reporting and inducing studies are. We compared reporting and inducing studies on a number of criteria, namely the mean and SD of the PI-R total scores, mean age, percentage of males, and percentage of Caucasians from each sample. Moreover, these comparisons were conducted separately for studies with clinical and non-clinical samples. Table 4 shows the results.
Comparison of studies reporting and inducing reliability.
Notes. nI and nR = sample sizes of inducing and reporting studies, respectively. t = t-test for comparing two means. p = probability level associated to the t-test. d = standardized mean difference.
Regarding non-clinical samples, statistically significant differences were only found for the SD of test scores (p = .002). In particular, reporting studies showed a larger SD on average than inducing studies, with a standardized mean difference reflecting a high magnitude.
Regarding clinical samples, there was no evidence of differences between studies inducing and reporting the reliability on the sample characteristics examined.
DiscussionThe reliable assessment of the symptoms of OCD is crucial for research, clinical and screening purposes (Abramovitch et al., 2019; Baruah et al., 2018; Mohsen et al., 2021). In this paper we focus on the reliability of test scores, that usually varies in each administration of the same instrument. RG meta-analyses collect data from the empirical studies that applied a given test, in order to estimate the average reliability of the test scores, identify study characteristics associated to the variability among the reliability coefficients, and provide reliability expectations in future applications of the test. In this paper we carried out an RG meta-analysis on the PI-R (van Oppen et al., 1995). We found and retrieved 118 studies that had applied the PI-R, of which 30 studies (33 independent samples) reported original alpha and/or test-retest reliability coefficients.
It is widely accepted that alpha coefficients of test scores must be over .70 for exploratory research, over .80 for general research purposes, and over .90 for clinical practice (Charter, 2003). In our RG met-analysis, the average coefficient alpha for the PI-R total score was .92, a remarkably high value. However, the 95% prediction interval was very wide, with limits .86 and .97, suggesting substantial uncertainty around the expected value of reliability estimates (alpha coefficients) calculated in future studies using the PI-R. As a consequence, we can conclude that, on average, the PI-R total score showed an excellent internal consistency for both research and clinical purposes, although exhibiting a large variability across studies. Out of the five subscales of the PI-R, Washing, Checking and Rumination showed average internal consistencies over .80, clearly good for research purposes; whereas Impulses and Precision subscales showed a fair average internal consistency, still useful for exploratory purposes. The large heterogeneity exhibited by the alpha coefficients across studies in all subscales is an indicator of the uncertainty in the expected reliability if a new study is conducted. In particular, it is important to note that Impulses, Washing, and Precision subscales yielded prediction intervals whose lower limits were under the cutoff point of .70. This raises concerns around the internal consistency of those subscales, even for general research purposes. Regarding test-retest reliability, the PI-R total scores showed a relatively high mean of .90 that should be interpreted with caution, as it was based on only two studies.
The results of our RG meta-analysis on the PI-R can be compared with those of previous RG meta-analyses on the most relevant instruments to measure obsessive-compulsive symptoms. Table 5 shows the averages of alpha and test-retest coefficients for the Maudsley Obsessive-Compulsive Inventory, MOCI (Sánchez-Meca et al., 2011), the Yale-Brown Obsessive-Compulsive Scale, Y-BOCS (López-Pina et al., 2015), PI (Sánchez-Meca et al., 2017), PI-WSUR (Rubio-Aparicio, Núñez-Núñez et al., 2020) and PI-R scales, and their corresponding subscales. The original PI and its two shorter versions, PI-WSUR and PI-R, showed an excellent similar internal consistency for the total scores. This provides evidence that, on average, the shortened versions PI-R and PI-WSUR yielded scores as reliable as those obtained with the original PI. In addition, these averages were larger than those of the MOCI and Y-BOCS total scores. Regarding temporal stability, the average test-retest reliability of the PI-R total scores was larger than those of the other four instruments, although this finding is based on only two studies. In sum, our data indicate that the PI-R scores present excellent reliability similar or superior to that of the other obsessive-compulsive scales, although with large heterogeneity across studies.
Mean alpha coefficients and test-retest reliability for the total scale and subscales to assess OCD.
k = number of studies. α+ = mean coefficient alpha. r+ = mean test-retest reliability coefficient.
Due to the large heterogeneity exhibited by the alpha coefficients of the PI-R across studies, we searched for moderator variables. However, and perhaps due to the small number of studies reporting original reliability estimates, the standard deviation of the PI-R total scores was the only factor yielding a statistically significant association with the alpha coefficients. Specifically, as expected from the psychometric theory, the standard deviation of test scores showed a significant positive relationship with alpha coefficients, which means that samples with larger variability among the test scores provided higher reliability estimates. Moreover, the ANOVAs revealed average alpha coefficients close to or above the cut-point of .90 regardless of the factor used for grouping. This finding supports that, in terms of reliability, the PI-R scale is appropriate both for clinical decisions and research purposes regardless the test version (the original in Dutch or its versions in other languages), the continent in which the scale is applied (Europe, North America or Asia) or the target population (community, undergraduate, clinical or a mixture of populations).
Our results enabled us to propose a predictive model of the reliability taking the SD of the total test score as the only predictor, namely with the equation α′=1−e−(1.833+0.034*SD). In our RG meta-analysis, the SDs of the studies ranged from 15.31 to 38.12. For these extreme SDs the predictive model offers predicted alpha coefficients of .90 and .96, respectively. A researcher intending to conduct an investigation in which the PI-R will be applied may use this predictive model to estimate the expected reliability, or to compare the actual alpha coefficient of the PI-R in a given study with the model predictions.
When a test is administered to a sample of participants, reliability should be estimated with the data at hand. In our RG meta-analysis, 74.6% of the studies either induced reliability from previous studies (reliability induction by report) or did not even mention reliability throughout the manuscript (reliability induction by omission). This implies that the malpractice of reliability induction affects three quarters of the empirical studies that have applied the PI-R so far, a very high value that has not significantly decreased in the most recent studies (we report a reliability induction rate of 77.8% in the 2016-2020 period). Other RG studies have found reliability induction rates as high as 77.5% (Sánchez-Meca et al., 2017), 94% (López-Pina et al., 2015), or 53.7% (Rubio-Aparicio, López-López et al., 2020). This indicates that the malpractice of inducing reliability is widely extended among researchers and practitioners. Our study, like most RG meta-analyses, contributes to the numerous initiatives and guidelines developed to make researchers aware of the need to report reliability estimates of test scores with the data at hand (Appelbaum et al., 2018).
The large reliability induction rate in our RG study (74.6%) compromises the generalization of our results to the total population of studies that applied the PI-R. In fact, the results of an RG meta-analysis may suffer from reporting bias if the magnitude of the reliability estimate obtained drives the decision to report it or not (Sterne et al., 2011). To assess the risk of reporting bias in our RG meta-analysis, the composition and variability of the samples in the inducing studies was compared to that in the reporting studies. Regarding non-clinical samples, statistically significant differences were found for the standard deviation of test scores. For clinical samples no differences were found between inducing and reporting studies. Therefore, the results of our RG study can be reasonably generalized to all studies that applied the PI-R to clinical samples. However, for nonclinical samples, our conclusions should be restricted to the reporting studies only.
The low number of empirical studies included in our RG meta-analysis, limits the scope of our analyses and the generalizability of the results. One possible reason is the inclusion of articles written in English only, potentially discarding other relevant records. Regarding temporal stability, only two studies reported test-retest coefficients, which is clearly insufficient to generalize the test-retest reliability results to future applications of the PI-R, as well as to examine moderator variables that could affect the magnitude of test-retest estimates. Regarding internal consistency, the distribution of 28 alpha coefficients for the total score of the PI-R was analysed, and the standard deviation of the PI-R total scores was the only factor statistically associated to the alpha values. However, the test for model misspecification suggests the existence of residual heterogeneity that was left unexplained by this parsimonious model. Another limitation was that the low number of alpha coefficients prevented moderator analyses for the subscales of the PI-R.
Regarding future empirical studies applying the PI-R, researchers should abandon the erroneous practice of inducing reliability from previous studies. Rather, the reliability of the test scores should be estimated with the data at hand for both the PI-R total score and its subscales. More empirical studies are needed that report alpha coefficients and specially test-retest estimates, so that future RG studies can examine in detail the factors associated to the variability of the internal consistency and temporal stability through different applications of the PI-R. At this stage, our study provides evidence that higher reliability estimates can be anticipated in samples that are more diverse with regards to the severity of OCD symptoms.
Finally, it is worth noting that this RG meta-analysis, like most RG meta-analyses published so far, was not pre-registered. Pre-registration is an open science practice that favors the transparency and reproducibility of scientific studies, and hence it should be encouraged in all research areas, including RG studies.
ConclusionsThe PI-R scores showed, on average, an excellent reliability for research and clinical purposes, similar to that of the PI and PI-WSUR scores, and similar or superior to that of the MOCI and Y-BOCS scores. However, the width of the prediction intervals revealed large heterogeneity across studies, and therefore substantial uncertainty regarding the expected reliability if a new study is conducted. The standard deviation of PI-R scores presented a positive statistically significant relationship with the alpha coefficients through multiple applications of the test. Researchers should provide original reliability estimates every time the PI-R or any other psychometric instrument is used, regardless the objectives of the study.
This research was funded by Agencia Estatal de Investigación (Spanish Government) and by FEDER funds, AEI/10.13039/501100011033, projects n° PID2019-104033GA-I00 and PID2019-104080GB-I00.
Note that although Vriend et al.’s (2013) study did not report any reliability estimate with the data at hand, it was included because we were able to calculate a posteriori the test-retest coefficient from the data reported.
The database with the 29 studies (33 independent samples) can be obtained from the corresponding author upon request.