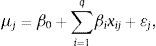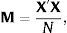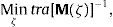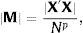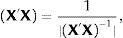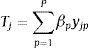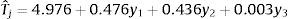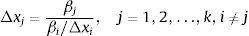Conjoint analysis has become the most used technique for measuring preferences for new products to be launched in the market. Experimental design models are key elements for its use in market research. Such models involve a matrix in which attributes and levels are combined, making product concepts that respondents then evaluate.
Experimental design has emerged as a key element in conjoint analysis’ success because its application generates statistical and reliability implications for part-worth factor estimations and for the type of heuristics followed by respondents.
This paper proposes a conceptualization of both statistical and cognitive efficiency criteria for experimental designs. A review of the most used statistical optimization criteria is presented, as well as a methodology for optimizing cognitive efficiency. Finally, we suggest a dynamic algorithm for optimizing the objective function in a sequential manner.
Conjoint analysis (CA) has been one of the most successful market research techniques in the last 40 years and one of the reasons that explains this is the continuous interaction between academic theory and professional implementation (Bradlow, 2005; Green, Krieger, & Wind, 2001). Its success is not only due to the technical upgrade linked to its application in studies on consumer preferences among products with multiple attributes, but also to its versatility, which has permitted its application in diverse fields such as marketing, transport management, financial services (Green et al., 2001), and even oncological studies (Beusterien et al., 2014).
Although the statistical foundations of experimental design were developed throughout the 1920s by Ronald Fisher, it was not until the 1970s that researchers began to use it in psychology and, soon after, in consumer behaviour and market research studies (Gustafsson, Herrmann, & Huber, 2007). However, despite the numerous investigations in which CA has been used (e.g. when someone introduces the term ‘conjoint analysis’ in the ‘Web of Science’ there are more than 3000 references) and the amount of methodological innovations that have been proposed, such as adaptive conjoint analysis (Johnson, 1987) or polyhedral designs (Toubia, Simester, Hauser, & Dahan, 2003), there are some issues in conjoint experimental designs that remain unresolved. These include the criteria for choosing the number of attributes and the reasons for using an experimental design and no other (Bradlow, 2005).1
This paper attempts to deepen the analysis of these two problems from a dual perspective: firstly, through the consideration of an efficient statistical solution and, secondly, taking into account the cognitive burden of these designs and its effect on responses. The literature proposes different criteria and ways to qualify an experimental design as efficient and each criterion determines the type of design recommended and the type of analysis to be used on the data gathered. Although different methods have different structures and philosophies, they nevertheless share some common elements: firstly, they all use the statistical design of experiments to develop the experimental design and, secondly, they all consider a compensatory model of consumer behaviour that, moreover, considers this behaviour as independent of the experimental design (Johnson & Meyer, 1984). Although the first common element in experimental design appears to remain valid, the second has received numerous criticisms (Olshavsky, 1979; Payne, Bettman, & Johnson, 1988). In this paper, we review the most common criteria used to determine experimental design efficiency, as well as their advantages and disadvantages, and, in addition, we propose a methodology to estimate the cognitive efficiency of experimental designs.
The study is arranged in the following sections. Firstly, we present some of the most important concepts of experimental design in CA. Secondly, we describe the most common methods for determining statistical efficiency in experimental designs. We then propose a system for evaluating the cognitive efficiency of experimental designs, which is illustrated with an example. Finally, some conclusions and possibilities for further research are presented.
Experimental design in conjoint analysisExperimental design is a numerical arrangement that combines attributes and levels to form stimuli (concepts of products or services), which later, in field work, must be evaluated by respondents. There are several ways of organizing stimuli, with full factorial designs being the easiest because they simply require presenting all possible level and factor combinations.
Experimental design is represented by an n×k matrix, where n are rows indicating the profiles generated and k are columns indicating the level variations of the attributes. If you use combinatory laws in the design, it is called a statistical design (Box, Hunter, & Hunter, 2005). However, statistical designs pose a major problem since as new attributes are added to the experimental design (even if they have only 2 or 3 levels), the number of combinations grows exponentially. For example, a statistical design in which there are 4 attributes with 3 levels each generates an experimental design of 81 profiles (34=81). Such a number of alternatives can overwhelm the cognitive ability of any interviewee (Green & Srinivasan, 1990). For this reason, researchers use fractional factorial designs, which are simply portions of a full factorial design. This reduces the number of alternatives that each interviewee has to assess, but researchers must pay the price of sacrificing the ability to estimate certain interactions. A price which, in some cases, could be very high, as for example in the research of new products associated with the sensory perceptions of respondents (haircare and cosmetic products) where two-factor interactions are very important (Green & Srinivasan, 1990).
Therefore, it has been shown that CA works quite well when a moderate number of attributes is considered for each profile within the experimental design, for example, less than 8 (Bradlow, 2005). But when the number of attributes is high, for example, more than 15, respondents’ cognitive capacity is overwhelmed and they use non-compensatory heuristics to choose profiles (Hauser, 2014; Johnson & Meyer, 1984). However, many technological products, such as laptops, digital cameras, and even cars or tourist services, use a large amount of attributes in their advertising to differentiate themselves from competitors (Bradlow, 2005; Netzer & Srinivasan, 2011).
In order to address this problem, several solutions have been proposed, in some cases hybrid solutions using a combination of techniques in a single study. For example, this is the case in the use of adaptive conjoint analysis (Johnson, 1987) or, more recently, adaptive self-explicated approaches (Netzer & Srinivasan, 2011). These methods follow two stages: in the first stage, respondents must complete a self-explicated survey (compositional study) where different attributes and levels are measured with the aim of reducing their number to the most relevant and, in the second stage, there is a conjoint experiment (decompositional study) to estimate the part-worth of the factors.
Now, for any of these experimental designs to generate valid and reliable data they must follow two basic principles: orthogonality and balance (Chrzan & Orme, 2000). An experimental design is orthogonal if all main effects and interactions can be calculated as independent variables (i.e. without correlation between them), and it is balanced when each level of each factor is repeated the same number of times in the overall experiment. When an experimental design is orthogonal and balanced at the same time, it is said that it is optimal (Kuhfeld, Tobias, & Garrat, 1994). However, when an experimental design is formed by factors with different ranges of levels (i.e. factors have 2, 3, 4, or 5 levels combined in the same design), it is very difficult to make fractions that are both orthogonal and balanced. Therefore, there is no other option than to use quasi-orthogonal designs (Kuhfeld, 1997) and, in this case, it is necessary to have some measure of their efficiency.
Criteria of efficiencyIn recent years, the literature has shown great concern around finding and developing efficient statistical designs (Vermeulen, Goos, & Vandebroek, 2008). A design is considered efficient when it gets the most and best information possible with the least number of interviewees and with the shortest time dedicated to field work (Louviere, Islam, Wasi, Street, & Burgess, 2008). However, knowing the researcher's objectives and assumptions is a prerequisite for trying to achieve efficiency in an experimental design. That is, whether the researcher considers interactions between factors or not, and the extent of these interactions, or, if they take into account the type of protocol used to gather information; i.e. if she or he uses verbal descriptions, images, or combinations of both. This means that the same experimental design can be efficient with regard to one criterion but not another. But the literature that discusses design efficiency only considers statistical efficiency (Kuhfeld et al., 1994; Vermeulen et al., 2008).
Kiefer (1959) was the first to propose the statistical efficiency concept as an instrument to compare and evaluate experimental designs and he described it using the so-called ‘theory of optimal design’. The idea was to try to gather all of a statistical design's goodness-of-fit in a figure, i.e. to transform design variance and covariance into a number, facilitating the comparison of various experimental designs and choosing the design that minimizes or maximizes that number. In addition, there are some criteria that depend on the objectives pursued by each researcher. For example, the researcher might only be interested in the estimation of main factors or she might also be interested in two-factor interactions, and in each case she must use different criteria to optimize the design.
The different criteria are represented by letters following alphabetical order, among the most cited are criteria A and D (Kuhfeld et al., 1994; Vermeulen et al., 2008) and, moreover, they are also the most used by the software packages (Kuhfeld, 1997; Myers, Montgomery, & Anderson-Cook, 2009). However, although the enormous virtues offered by computer-generated designs are recognized, especially because they are easy to get, there are some authors who criticize how they are used indiscriminately and without taking into account the criteria behind the design or, therefore, the type of adjustment that can be achieved with the design obtained (Myers et al., 2009). Thus, knowing the basic characteristics of these designs can help researchers to select one criterion or another depending on the main purpose of the research and bearing in mind the limitations that each criterion entails.
The optimization criteria are based on the moment matrix. To illustrate its operation, we assume that a conjoint experiment was carried out, it was coded following a vectorial form, and in it respondents rated each profile from 1 to 10. In addition, it was assumed that these scores reflected respondents’ preferences in a linear model of part-worth attributes (Johnson & Meyer, 1984). In this case, the easiest way to estimate the part-worth of factors is to adjust them by linear regression, where the dependent variable μj gathers the scores assigned to each profile for j={1, …, n}:
where xij are experimental design combinations, βi are part-worth estimates representing factor slopes, and ¿j is the error. In matrix notation, it can be expressed as μ=α+βX+e, X being the experimental design matrix coded in vector form (−1, 0, 1). Efficiency criteria are based on the so-called moment matrix M, which is defined as:where X′X is the product of the transposed matrix multiplied by the normal matrix from the experimental design and N is the number of profiles.The A-optimal criterion only considers variance as a relevant element for defining efficiency. This criterion consists of calculating the sum of variances of the model parameters and it is the same as the sum of diagonal parameters, or the trace, of (X′X)−1. This means that the A-optimal criterion prioritizes main factor estimations without taking into account interactions that are reflected in covariance. Therefore, the optimization criterion consists of choosing the experimental design that minimizes the trace of the inverse moment matrix and it will be defined by:
where tra represents the trace of the moment matrix, i.e. the sum of coefficient variance, and ζ represents the design used.The other most used criterion is the D-optimal criterion (Toubia & Hauser, 2007; Vermeulen et al., 2008). This also seeks to find the experimental design that improves parameter estimation, but in this case, besides the main factors, it also includes interactions. This criterion requires calculating the determinant of the moment matrix:
where p is the number of model parameters (which can be main factors, two-factor interactions, three-factor interactions, etc.) and N is the number of profiles analysed. If we assume that errors follow a normal distribution, independent and with constant variance, the determinant of the moment matrix (X′X) is inversely proportional to the confidence intervals of coefficients in the regression model, and this reflects how well these coefficients are estimated. In this case, a small value in |X′X| implies a poor estimate of β (Myers et al., 2009). Thus, a design is D-optimal if it minimizes the determinant of the moment matrix (4), which is the same as the inverse of the determinant of the variance and covariance matrix:Therefore, the aim of the D-optimal criterion is to establish which experimental design minimizes both variance and covariance. Furthermore, due to the fact that this criterion uses the power p (number of parameters to be estimated) in the calculation of the determinant of the moment matrix, it allows for use of the D-optimal efficiency criterion to compare experimental designs of different sizes.
In short, whether we use A-optimal or D-optimal criteria, if we have a balanced and orthogonal experimental design its efficiency will be optimal for both, and when we analyse quasi-orthogonal designs they will be more efficient as they tend towards balance and orthogonality. These criteria measure the design's goodness-of-fit in relation to a hypothetical orthogonal design, which it is not possible to use for multiple reasons. However, these measures should not be considered as absolute measures of design efficiency, but as relative tools to compare one design with another. An efficient design must fulfil the following requirements (Kuhfeld, 1997):
- •
A design is orthogonal and balanced when the moment matrix M is diagonal.
- •
A design is orthogonal when the sub-matrix M, excluding the row and column for the intercept variable, that is to say α, is diagonal.
- •
A design is balanced when all off-diagonal elements, all row and column interceptions, are zero.
- •
A design's efficiency increases as diagonal absolute values become smaller, that is to say, as Np becomes larger.
If a full factorial design is orthogonal and balanced (i.e. the moment matrix M is diagonal), it is possible to use the A-optimal or D-optimal criteria indifferently. However, if the design is fractional factorial will be some off-diagonal values, it must be the researcher who decides if she is interested only in main factor estimations, thus using the A-optimal criterion, or if she is also interested in two-factor interactions, in which case the best approach would be to use the D-optimal criterion.
The goal pursued by Kiefer (1959) of reducing the statistical goodness-of-fit of an experimental design to a single number has been criticized as overly ambitious and, therefore, these criteria should be considered as one of many other relevant aspects, but not as a definitive measure (Myers et al., 2009). On the other hand, CA literature has also criticized that accepting these criteria as valid involves the assumption that respondents value profiles using an algebraic utility function, where the assessment of each profile is based exclusively on the observed attributes, and that their assessment is independent of the number of profiles to be evaluated (Johnson & Meyer, 1984). In the same vein, but in choice-based conjoint analysis, Louviere (2001) warns that the use of increasingly efficient designs can generate unintended consequences in respondents’ answers due to their cognitive limitations, and they may therefore use heuristics other than the compensatory model during their selection process (Hauser, 2014).
In short, a statistically efficient experimental design does not guarantee the responses’ reliability or good predictive capability, since these will depend on the effort and sincerity of interviewees’ answers. CA is also used by academic researchers and market researchers who highly value the predictive capability of the models obtained. On the other hand, if the data gathered are not accurate, they can lead to misdiagnoses and, thus, to erroneous advice about management policies (Salisbury & Feinberg, 2010). Therefore, when an experimental design is developed we should not only take into account its statistical efficiency, but should also incorporate some criteria to measure its cognitive efficiency.
Determinants of cognitive effort in experimental designsA common issue in CA literature is understanding how experimental designs determine the cognitive effort that respondents have to make and how their effort affects response reliability and its predictive capability. In particular, from a cognitive perspective, what would be the optimum size of a choice set?
Different theoretical approaches have proposed different behavioural models depending on their theoretical axioms. For example, economic theory considers that if a consumer has a large number of profiles to choose from, this large choice set improves her likelihood of finding a profile with level-factor combinations that better fit her preferences (Lancaster, 1990). However, this rational model has been criticized from the perspective of other theoretical frameworks. Johnson and Meyer (1984) advocate the opposite: that it is better to maintain choice sets with a small number of profiles because a larger amount would have negative statistical and cognitive effects (see also DeShazo & Fermo, 2002; Louviere et al., 2008). From the statistical point of view, having many attributes (whether profiles or levels) in a choice set reduces the amount of data available for each attribute, undermining their weight and the accuracy of estimates (DeShazo & Fermo, 2002). In fact, as noted above, Bradlow (2005) considers that CA works relatively well with around 8 attributes per profile and that problems begin to be generated from 15 attributes and beyond.
Regarding cognitive effects, information processing theory considers that people have limited rational capacity and that when they face a decision-making process, the greater the number of alternatives, the greater the difficulty in processing, calculating, and storing all the information generated throughout the process (Simon, 1990). According to Johnson and Meyer (1984), the complexity of a choice is determined by the number of cognitive steps that each respondent has to take to carry out an evaluation and make the appropriate decision, comparing all of the alternatives. For example, if a consumer compares two photographic cameras defined by two attributes (one has ‘the capacity to take 300 pictures’ and one is ‘pocket-size’) the respondent has to make at least three assessments or ‘cognitive steps’ in Johnson and Meyer's terms: (1) assess if ‘the capacity to take 300 pictures’ is a good attribute; (2) evaluate if ‘pocket-size’ is also a good attribute; and (3) compare the two attributes and decide which one is best; as the number of attributes increases, the number of assessments and ‘cognitive steps’ also increases. Because the respondent comes to have difficulties in her evaluation of attributes one by one, she begins to use an alternative criterion of simplified heuristics such as the lexicographic heuristic or elimination by aspect (Hauser, 2014; Payne, 1982). As a result of using inconsistent responses and of not using the compensatory model, the linear model estimates will generate a poor fit (Payne et al., 1988).
A proposal to optimize cognitive effort in experimental designsIn this study, we make use of the cognitive complexity concept proposed by Johnson and Meyer (1984) and we also use the information acquisition cost function proposed by Grether and Wilde (1984). Both criteria where considered for optimizing an experimental design taking into account all steps taken by a respondent in making the appropriate decision. To achieve this optimum it is necessary to determine the number of profiles, factors, and levels that minimize the cost of the whole assessment process of a choice set.
One useful criterion for estimating the cost of cognitive effort has been the time spent on making a decision (Dellaert, Donkers, & Soest, 2012; Grether & Wilde, 1984; Johnson & Meyer, 1984). The time spent on a decision remains a recurring issue both in consumer behaviour studies (East, Wright, & Vanhuele, 2013) and in experimental design studies (Louviere et al., 2008). For example, in a classic experiment, East (1973) showed that respondents needed more time to choose between two alternatives than between three when the choice task was difficult and less time when the choice task was easier. This means that choosing between a larger number of profiles does not always require more time than choosing between a smaller number. However, time is a variable that is very closely related to effort (Grether & Wilde, 1984).
Besides, it is also important to consider the time taken to complete the questionnaire, because this can have negative consequences on respondents’ behaviour: the longer the time required to do the interview, the lower the willingness to participate and the greater the chance of it being left unfinished (Netzer & Srinivasan, 2011; Scholz, Meissnery, & Decker, 2010). It is clear that as the experimental design's complexity increases (the choice set changes from 2 to 4 and then to 6 cameras), so does its duration (Grether & Wilde, 1984). In the formation of the cognitive complexity of an experimental design three variables are involved: the number of scenarios, the number of attributes, and the number of levels. In most cases, these three variables can have different weights during the time required to fill in the questionnaire (Johnson & Meyer, 1984).
Every factorial design, whether fractional or arranged in blocks, draws from a full factorial design. If we define the subset of profiles that form the choice set as Sr, r=1, …, q, the number of factors of each profile as Ci, i=1, …, n, and the number of levels of each factor as Wj, j=1, …, m, the number of Johnson and Meyer's cognitive steps would be determined by SrΠWj, Π being the product from j to q levels. Since time is related to effort (Grether & Wilde, 1984), the time required to evaluate the choice set will depend on the number of cognitive steps. Moreover, in the case that all the factors have the same number of levels, the time taken can be expressed as a function of the three elements: time=f(Wj, Ci, Sr)=Wj×Ci×Sr. Nevertheless, if we apply logarithmic transformation the model becomes additive:
where Tj is the Napierian logarithm of time, βp is the part-worth of variable p, indicating the slope, and yjp is the Napierian logarithm of the three independent variables.Given the diversity of subjects and ways to present profiles to respondents (described by text, by paragraphs, by pictures, etc.) and the variety of contexts in which the research can be based (Payne, 1982), it is reasonable to think that a way to estimate the weight each item has in the experiment's duration is by trial and error, because the models estimated in one context can hardly be appropriate in another context (Johnson & Meyer, 1984). In the present study, we follow this logic and we propose response surface methodology (RSM) as an algorithm to optimize the cognitive effort in an experimental design.
RSM is a statistical technique used in the development, improvement, and optimization of industrial processes and it has recently been incorporated into market research studies (Huertas-Garcia, Gázquez-Abad, Martinez-Lopez, & Esteban-Millat, 2013). The methodology was proposed in the early 1950s by Box and Wilson (1951), who justified its use on the basis of the need for efficient experimental procedures that were able to determine the operating conditions of a set of controllable variables. It was considered as a methodology with which an optimal response could be achieved (Box & Draper, 1987). However, it was not developed until the 1970s when some statistical restrictions were overcome and the use of software packages for calculation became widespread (Myers et al., 2009).
RSM is an experimental process that involves sequential stages in which the information obtained in the first stage serves for planning and executing the following stages (Raghavarao, Wiley, & Chitturi, 2011). Nowadays, with the development of market research on the Internet, these sequential models are particularly suitable because they allow for programming questions based on previous answers and, also, can be tailored in real time (Netzer & Srinivasan, 2011; Scholz et al., 2010). The experimental sequence of RSM consists of several stages, beginning with a first-order model (i.e. a flat representation) to delimit the slope toward the optimal region and, next, further experiments are developed until reaching the optimum. The algorithm can be summarized in the following five steps (Myers et al., 2009):
- 1.
A first exploratory experimental design of an orthogonal type is proposed and is fitted with a first-order model. For this, two-level vector encoding including a centre point is recommended.
- 2.
Steps are calculated using the first stage's estimated values and ‘the fastest route to the minimum’ is delimited.
- 3.
Several experiments are carried out throughout the process, noting that the response values decrease, until reaching a point where they begin to grow again; that is, until reaching a turning point.
- 4.
In the case that greater precision were required, the turning point is taken as the basis for developing new experiments to better fit the trend. The adjustment model may continue to be a first-order model.
- 5.
However, if it is noticed that the curvature degree is high, using a second-order model is recommended.
The procedure is designed to achieve independent variable combinations that allow for obtaining highly accurate optimum response values. However, market studies usually do not require such extreme degrees of accuracy given the subjective nature of responses and, therefore, with few experiments it is possible to achieve reasonably accurate approximations to the optimum.
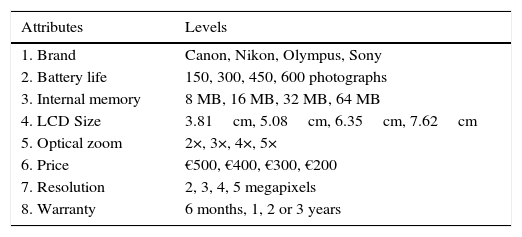
ExperimentThe experiment was inspired by the work of Netzer and Srinivasan (2011), who propose the assessment of digital camera profiles (Table 1 shows the attributes and levels considered), although they use a completely different methodology to ours. While they rely on an adaptive self-explicated model for measuring part-worth attributes (a compositional model), in our case we propose the RSM algorithm (a type of decompositional model). In order to arrange the experimental design we departed from a fractional factorial design, specifically from a half factorial design (as can be seen in the first four columns of Table 2). This experimental design has enough variations of profiles, attributes, and levels to contribute to a significant estimation of the factors’ part-worth using, as a response variable, the time taken by respondents to assess the camera choice set (Table 3).
Attributes and levels of digital cameras.
| Attributes | Levels |
|---|---|
| 1. Brand | Canon, Nikon, Olympus, Sony |
| 2. Battery life | 150, 300, 450, 600 photographs |
| 3. Internal memory | 8 MB, 16 MB, 32 MB, 64 MB |
| 4. LCD Size | 3.81cm, 5.08cm, 6.35cm, 7.62cm |
| 5. Optical zoom | 2×, 3×, 4×, 5× |
| 6. Price | €500, €400, €300, €200 |
| 7. Resolution | 2, 3, 4, 5 megapixels |
| 8. Warranty | 6 months, 1, 2 or 3 years |
Source: Adapted from Netzer and Srinivasan (2011).
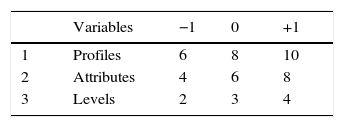
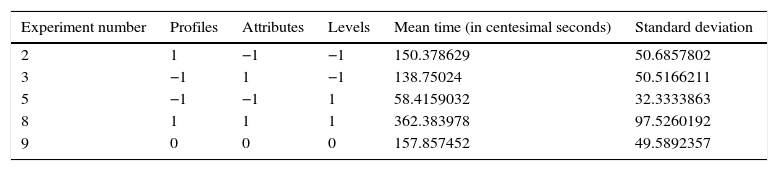
In the experiment, we considered three-factor combinations according to the experimental design to gather data from respondents’ time spent on making their assessments. In addition, we also manipulated all three factors (profiles, attributes, and levels) around their mean value. These items of information were taken from the work of Netzer and Srinivasan (2011), in which the average number of profiles was 8, for attributes it was 6, and for levels it was 3. This sets a 23 factorial experiment around the average point, that is, nine experiments (8 derived from the factorial design plus the central point), and all of them are encoded in vector form (the coding arrangement of the three factors is shown in Table 1). However, due to resource constraints, we have estimated a half factorial design, 23−1 plus the centre point, i.e. 5 profiles. The literature recommends thinking about this first result as the point of origin, ‘as a confirmation test, to ensure that conditions experienced during the original experiment have not changed’ (Myers et al., 2009, p. 186) (Table 2).
In order to gather data, a sample of 250 undergraduate students from a large university in Barcelona was used, it was randomly divided into 5 groups and 234 valid questionnaires were obtained (45–48 per group). Each respondent was invited to a computer room and, following researchers’ instructions, evaluated a set of digital camera profiles, to which attributes and levels were assigned following the experimental design in Table 2. At the begin of this exercise, respondents had to indicate the exact time registered on the computer clock, then make their assessment of the choice set of digital cameras using a rating score of 1–10 (1 being the least preferred and 10 the most preferred), after their evaluation they had to indicate, once again, the exact time on the questionnaire, and, finally, fill in some identification information and other control questions. Among the control questions, one asked respondents their assessment of the study and another was related to what they thought the objective of the study was. In order to arrange all the different choice set scenarios, which ranged from 6 to 10 profiles, the SPSS orthogonal design generator was used. The study was carried out between February and March 2014. No respondents thought that the study's objective was to measure the time taken; all of them thought it was for measuring their preferences in the digital camera set.
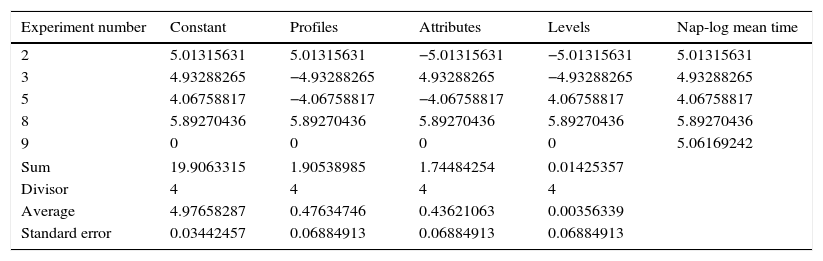
As a dependent or response variable, we used the stated time taken to perform the assessment of the digital camera choice set. To make the calculation easier, the time measured in 60s was transformed into 100s, we then calculated the average time of each group, measured in centesimal seconds. Next, this was converted into its natural logarithm and, finally, to calculate the part-worth values the table of contrast coefficients was used. This is a very simple method for estimating the slope of the main factors, given that when the vectorial coding system used with independent variables (a combination of −1 and 1) is transformed into the moment matrix it becomes an identity matrix and, therefore, the regression model to fit is simply y=Xb. In other words, the coding matrix is multiplied by the vector of results to obtain a finding matrix, then, by adding the values of each column and dividing them by the number of positive and negative coded levels, it is possible to obtain the part-worth values as though adjusted by OLS (Table 4 illustrates the calculations). In order to calculate the standard error, we followed the process of estimating the average variance proposed by Box et al. (2005).
Contrast coefficients calculation table.
| Experiment number | Constant | Profiles | Attributes | Levels | Nap-log mean time |
|---|---|---|---|---|---|
| 2 | 5.01315631 | 5.01315631 | −5.01315631 | −5.01315631 | 5.01315631 |
| 3 | 4.93288265 | −4.93288265 | 4.93288265 | −4.93288265 | 4.93288265 |
| 5 | 4.06758817 | −4.06758817 | −4.06758817 | 4.06758817 | 4.06758817 |
| 8 | 5.89270436 | 5.89270436 | 5.89270436 | 5.89270436 | 5.89270436 |
| 9 | 0 | 0 | 0 | 0 | 5.06169242 |
| Sum | 19.9063315 | 1.90538985 | 1.74484254 | 0.01425357 | |
| Divisor | 4 | 4 | 4 | 4 | |
| Average | 4.97658287 | 0.47634746 | 0.43621063 | 0.00356339 | |
| Standard error | 0.03442457 | 0.06884913 | 0.06884913 | 0.06884913 | |
The first-order model derived from the experiment is as follows:
where Tj is the Napierian logarithm of average time spent on the assessment process, y1 is the number of profiles, y2 is the number of attributes, and y3 is the number of levels. As we can see in Table 4, only the number of profiles and the number of attributes have a significant impact on the time used for assessment and both have a similar weight (β1=0.476 and β2=0.436), while the number of levels does not seem to have any effect on the amount of time used by respondents.Once the model has been fitted and the weight of the main factors has been estimated (7), we need to set the path to achieve the minimum value of Tj. To calculate the path to reach the minimum we followed the algorithm proposed by Myers et al. (2009):
In the first stage, we need to estimate the length of the steps that will be taken to reach the minimum; usually the length of the step is 1, say Δxi. This length is assigned to the independent variable whose part-worth is the highest in absolute value, in our case it is (β1=0.476).
We then estimate the length of the other variables’ steps, whose relative longitude will depend on the weight of each factor, following this function:
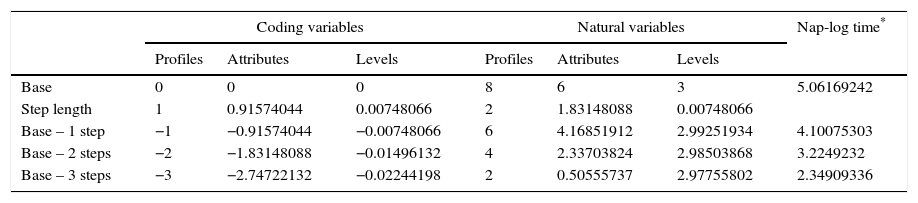
Finally, coded variables are transformed into their normal values. Each part-worth measures the slope degree that represents a change from 0 to 1 in the rating scale. For example, β1 represents the change from 0 to 1 that meant a change from 8 to 10 profiles, i.e. an increase of 2 profiles. In the case of β2, the slope represents the change from 6 to 8 attributes, i.e. an increase of 2 attributes, and, finally, β3 represents the change from 3 to 4 levels, this time with an increase of 1 level. As defined above, the step length for the main important factor (number of profiles) is 1, and this step generated an increase of 0.476 in the amount of time, which corresponds to a change in two profiles. For the other independent variables, the length of their steps is proportional to the values resulting from Eq. (3), as shown in Table 5.
Simulation process of RSM algorithm.
| Coding variables | Natural variables | Nap-log time* | |||||
|---|---|---|---|---|---|---|---|
| Profiles | Attributes | Levels | Profiles | Attributes | Levels | ||
| Base | 0 | 0 | 0 | 8 | 6 | 3 | 5.06169242 |
| Step length | 1 | 0.91574044 | 0.00748066 | 2 | 1.83148088 | 0.00748066 | |
| Base – 1 step | −1 | −0.91574044 | −0.00748066 | 6 | 4.16851912 | 2.99251934 | 4.10075303 |
| Base – 2 steps | −2 | −1.83148088 | −0.01496132 | 4 | 2.33703824 | 2.98503868 | 3.2249232 |
| Base – 3 steps | −3 | −2.74722132 | −0.02244198 | 2 | 0.50555737 | 2.97755802 | 2.34909336 |
In many cases, it is possible to find a good approximation to the optimum simply with the first simulation. Particularly in the case when all values are discrete levels, as in this study. As shown in Table 5, with the ‘base – 2 steps’, the simulation table finds a good approximation to the optimal solution. This is obtained with the combination of 4 profiles with 2 attributes each and 3 levels per attribute, and to complete this assessment respondents take 25.15 centesimal seconds (e3.22=25.15). In the following simulation, the ‘base – 3 steps’, the model suggests an impossible solution because in the combination of profiles, attributes, and levels it considers less than one attribute in the choice set. However, if instead of working with discrete values we were working with continuous values, it could be possible to obtain greater accuracy, simply by developing new experiments around the last point estimated. It could also be possible to use a second-order equation to fit the model, trying to cover the degree of curvature that is usually near the optimum.
In short, developing an experimental design to carry out CA research is not an easy task as it must fulfil two contradictory objectives: firstly, achieve statistical efficiency, helping to improve the parameters’ estimation, and, secondly, ensure effective and trusted answers from respondents taking into account their limited cognitive capability. With these arguments, using software for generating experimental designs is not a panacea, because the type of protocol used to collect data and the context in which the experiment is developed determine the behavioural pattern followed by consumers in evaluating profiles (Johnson & Meyer, 1984; Payne, 1982; Payne et al., 1988). Therefore, according to the advice of Kuhfeld et al. (1994), the best strategy for building an experimental design is to combine computer tools, which provide designs quickly and easily, with the researcher's insight to select the most appropriate design option for the context of the study.
ConclusionsCA has been one of the most common market research techniques used by researchers and practitioners to measure consumer preferences for more than four decades. This technique emerged to overcome some shortcomings in the use of self-explicated questionnaires, which had been criticized for being vague and unrealistic (Hauser & Rao, 2004; Sattler & Hensel-Börner, 2007). To implement CA, a fundamental step is building the experimental design, which determines the number of profiles that form the choice set and the pattern for arranging them by combining attributes and levels. To make these designs statistically efficient, they must be orthogonal and balanced, and this is only possible with very simple designs; i.e. those which require few variables and few levels. Therefore, most experimental designs are quasi-orthogonal and, in this case, it is necessary to measure their degree of statistical efficiency.
There are several ways to measure statistical efficiency. In this paper, we have reviewed the two most common optimization criteria in the literature: A-Optimal and D-optimal criteria. However, these criteria are based on the underlying assumption that an algebraic relationship between product attributes and utility explain consumer behaviour, and that this relationship is independent of the number of alternatives and of the experimental context. These assumptions have been criticized as unrealistic from the perspective of consumer cognitive behaviour theories. To overcome these cognitive limitations a cognitive efficiency criterion is proposed which can act as a complement to the statistical efficiency criterion. In addition, we have also proposed a function to estimate this efficiency and an algorithm to optimize it. The function is inspired by the cognitive steps proposed by Johnson and Meyer (1984), where the number of profiles, factors, and levels are independent variables, and the length of time to fill in the questionnaire is the dependent variable (Grether & Wilde, 1984). Using the time taken for the choice set assessment as an estimate of cognitive effort is completely appropriate since market research uses the Internet and websites where respondents’ patience tends to be low (Deutskens, de Ruyter, Wetzels, & Oosterveld, 2004) and their willingness to participate decreases as the length of the survey extends (Scholz et al., 2010). In addition, the algorithm proposed to optimize this function is RSM and to illustrate this whole process we carried out an experiment using digital cameras as stimuli for respondents to choose among them.
This study responds to the request made by Bradlow (2005) to develop techniques to assess consumer preferences, allowing, at the same time, for the evaluation of a large number of attributes without cognitively burdening respondents. Its contribution to the literature is threefold: firstly, experimental designs are conceptualized using both statistical and cognitive efficiency; secondly, a functional relationship between all the components of an experimental design (profiles, factors, and levels) is established, as well as an estimator of cognitive effort as target function; and thirdly, a sequential and dynamic algorithm is proposed that allows the objective function reach an acceptable optimum.
Hybrid proposals have emerged, such as adaptive conjoint analysis, with the aim of balancing statistical efficiency and cognitive effort. However, the fact of using partial profiles during the compensatory phase has been criticized by both scholars and market researchers for the inability to obtain stable factor estimations in individual studies (Orme, 2007). There have been some proposals (for example, Huertas-Garcia, Gázquez-Abad, & Forgas-Coll, 2016) in which partial profile scenarios are replaced with full profiles, but this solution is only viable for a small number of factors.
One limitation of this study is that the analysis has only focused on classical CA without considering discrete choice experiments, which are characterized by each respondent only choosing the best option from the choice set. Although choice has been defined as much more natural behaviour in consumption than ranking and rating (Louviere, Hensher, & Swait, 2007), the items of information gathered by the researcher from each respondent are minimal (1, if x alternative was chosen from the entire choice set, and 0 otherwise), therefore its use is restricted to studies that use very large samples. Another limitation in our study is that only the existence of a compensatory model in consumer choice processes was considered, regardless of the existence of other non-compensatory heuristic models (lexical, qualifying, etc.) that could explain the process of choosing among many alternatives.
Furthermore, due to lack of resources, the experiment was carried out with the following restrictions: firstly, it was performed once, so more replicas are needed to verify the results; secondly, in the initial phase of RSM only a half factorial design was developed and with this restriction it was not possible to estimate all two-factor interactions, which would have contributed to more interesting results; thirdly, the sequential experiments needed to follow the steps to reach the minimum were simulated assuming a linear trend between the factors. Therefore, possible further research could involve conducting new tests using a full factorial design in the first phase and carrying out all the necessary steps until reaching the optimum.
Although Bradlow (2005) points out nine problems in the use of conjoint analysis, in this study we have focused our analysis on two of them.