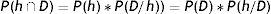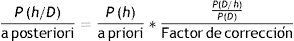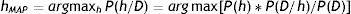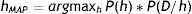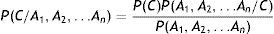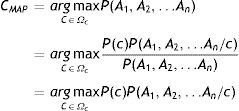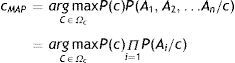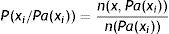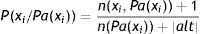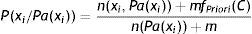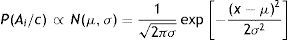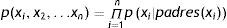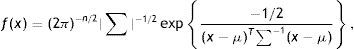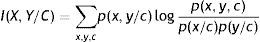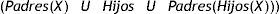En este artículo se aborda la forma de construir un clasificador eficiente a través de redes bayesianas utilizadas en la minería de datos y cuya finalidad es conseguir más precisión que otros modelos empleados en los problemas de credit scoring. El enfoque bayesiano, basado en modelos de probabilidad, emplea la teoría de la decisión para el análisis del riesgo eligiendo en cada situación que se presenta la acción que maximiza la utilidad esperada. Usando una muestra de datos bancarios reales se concluye la superior capacidad predictiva de estos modelos respecto a los resultados obtenidos por otros métodos estadísticos paramétricos y no paramétricos.
This paper analyses how to build an efficient classifier across Bayesians networks used in data mining. The purpose of using the Bayesian model is to improve credit scoring accuracy. The Bayesian approach, based on probability models, analyses risk by using the decision theory, yielding as a solution that action that maximizes the expected utility. Expert assessment may be included in the model. To show the superiority of the Bayesian approach, results obtained for real bank data are compared with those obtained with alternative parametric and non-parametric models.
En este artículo se presenta una forma de implementar un clasificador de préstamos bancarios a través del enfoque bayesiano. Con la información aportada por el cliente que solicita el crédito, aplicada a la base de datos histórica de que dispone el banco, el modelo sugiere al gerente una primera decisión sobre la aceptación o no de la petición del cliente (modelo de credit scoring). En este artículo se propone un sistema de predicción que optimiza la decisión estadística que determina la clase a la que pertenecen las muestras o clientes evaluados, siempre sin olvidar que los modelos de credit scoring ayudan en un primer momento a tomar la decisión de si conceder o no el crédito, e incluso permiten justificar la misma. No obstante, junto a sus resultados, deben considerarse otras dimensiones cualitativas que necesariamente deben complementar la toma de la decisión y que no se pueden estudiar con los modelos matemáticos.
Disponer de un buen método que nos ayude a tomar decisiones más correctas puede mejorar la eficacia de la gestión de una entidad bancaria, siendo de especial interés en una situación como la actual, en la que a las entidades financieras se les está exigiendo un mayor análisis del riesgo y una mejora en la eficiencia de su gestión.
Las formas de enfrentarse al problema de la clasificación son variadas. La gran diversidad de técnicas existentes pueden incorporar análisis estadísticos, herramientas de minería de datos o inteligencia artificial con aprendizaje de máquina; la técnica más clásica en los problemas de credit scoring ha sido la regresión logística, que generalmente ofrece buenos resultados estadísticos. Otro enfoque clásico es sintetizar la información de la base de datos de clientes a través de reglas y de árboles de decisión; finalmente, otras aproximaciones más novedosas empleadas en los modelos de credit scoring se basan en la aplicación de redes neuronales, implementando algoritmos evolutivos, splines de regresión adaptativa, las máquinas de vectores soporte o de la lógica borrosa. Una revisión de los métodos citados, así como una aplicación práctica, podemos encontrarlas en Bonilla et al. (2003).
En este trabajo se conjuga una adecuada selección de variables y un método eficiente de equilibrar la muestra, lo que, unido a la expresividad de las redes bayesianas, constituye un novedoso método de abordar el problema del credit scoring. Se demuestra la superioridad estadística de este método al comparar los resultados obtenidos con los provenientes de la aplicación de otros modelos paramétricos y no paramétricos como las redes neuronales, los árboles de decisión, las máquinas de vectores soporte o la regresión logística; se contrastan asimismo los resultados del modelo propuesto con los obtenidos por 6 modelos multiclasificadores y un método que incorpora una matriz de coste.
Los resultados del modelo propuesto se analizan con los datos originales, muestra desbalanceada, y con la muestra balanceada a través del algoritmo SMOTE (Synthetic Minoritary Over-sampling Technique) originario de Chawla et al. (2002) y del método del submuestreo equilibrado del Cubo, propuesto por Deville y Tillé (2004). Para la realización de este trabajo se ha dispuesto de una parte de la base de datos de los clientes de una entidad bancaria real que han solicitado un crédito en un determinado período de tiempo.
A continuación y, en primer lugar, se exponen de forma somera los métodos y redes bayesianas así como los principales algoritmos para su aprendizaje tanto de la parte cuantitativa como cualitativa; en la tercera sección se abordan 2 problemas fundamentales para el buen comportamiento de un clasificador: la selección de variables y el balanceo de la muestra. Posteriormente, en la cuarta sección se presentan los resultados obtenidos comparándolos con múltiples métodos y algoritmos de clasificación. Finalmente, se ofrecen las conclusiones de este estudio.
2Métodos bayesianosLas situaciones en las que los seres humanos toman decisiones se pueden clasificar según el conocimiento y control que se tenga sobre las variables que intervienen o influyen en el problema en 3 categorías: certeza, riesgo (se conoce el problema, se conocen las posibles soluciones, no se conocen con certeza los resultados que pueden arrojar, pero sí la probabilidad de que ocurra cada resultado) e incertidumbre (se posee información deficiente para tomar la decisión, no se tienen ningún control sobre la situación, no se conoce cómo puede variar o la interacción de la variables del problema, se pueden plantear diferentes alternativas de solución pero no se le puede asignar probabilidad a los resultados que arrojen)4. En la «teoría de la decisión» suele además clasificarse la incertidumbre como estructurada (no se sabe qué puede pasar entre diferentes alternativas, pero sí se conoce qué puede ocurrir entre varias posibilidades) y no estructurada (no se sabe qué puede ocurrir ni las probabilidades para las posibles soluciones).
El paso de situaciones de incertidumbre a situaciones de riesgo, es decir, la cuantificación de la probabilidad de que ocurra una determinada solución, es de vital importancia en la toma de decisiones económicas. En casos como el que nos ocupa entraña la diferencia entre el éxito o el fracaso de la empresa, ya que la principal actividad de una entidad bancaria es dar créditos a clientes, y si estos no son devueltos la quiebra de dicha entidad es inminente; por ello, la disponibilidad de un buen mecanismo que aventure la probabilidad de que un cliente devuelva un crédito es de capital interés para una entidad financiera; este mecanismo debe ser además de acceso relativamente sencillo (muchos puntos de venta o clasificación dirigidos por personal no especialmente cualificado), sin perjuicio de que incorpore módulos de mayor complejidad con acceso a los centros de dirección o puntos en los que se tomen las últimas o más importantes decisiones.
Los métodos y técnicas bayesianos aportan estas utilidades; se pueden considerar de construcción sencilla, con una semántica clara y tienen un enfoque sólido y elegante; han presentado tradicionalmente el problema de su elevado coste computacional, problema que el avance tecnológico está contribuyendo a resolver de forma rápida y eficaz.
Los modelos bayesianos sirven tanto para resolver problemas desde una perspectiva descriptiva como predictiva. Como método descriptivo se centran en descubrir las relaciones de dependencia/independencia. Desde esta óptica se puede afirmar que a veces complementan y/o incluso superan a las reglas de asociación. En cuanto a la función predictiva, se circunscribe a las técnicas bayesianas como métodos de clasificación.
Mitchell (1997) nos sugiere 2 razones de que los métodos bayesianos sean algunas de las técnicas que más se han utilizado en los problemas de inteligencia artificial, el aprendizaje automático y la minería de datos:
- 1.
Constituyen un método muy válido y práctico para realizar inferencias con los datos que disponemos, lo que implica inducir modelos probabilísticos que, una vez calculados, se pueden utilizar con otras técnicas de minería de datos.
- 2.
Son extremadamente útiles en la comprensión de otras técnicas de inteligencia artificial y minería de datos que no trabajan con las probabilidades de las que nos dotan las técnicas bayesianas. Esta combinación de métodos es muy provechosa para optimizar las soluciones de algunos problemas planteados en la minería de datos.
Para comprender estas técnicas bayesianas vamos a empezar con el teorema de Bayes. Definamos las siguientes expresiones:
- •
P(h) es la probabilidad a priori de que se cumpla la hipótesis h. Esta probabilidad contiene el conocimiento que tenemos de que la hipótesis h es correcta.
- •
P(h/D) es la probabilidad a posteriori de que se cumpla la hipótesis h una vez conocidos los datos D. Esta expresión refleja la influencia que tienen los datos observados sobre la hipótesis h.
- •
P(D/h) es la probabilidad de que los datos D sean observados en un escenario en el caso de que la hipótesis h sea correcta.
Sabemos que:
Por lo tanto:
Observando la expresión del teorema de Bayes sabemos que P(h/D) aumenta si se incrementa P(h) y P(D/h) o disminuye P(D).
Como ya disponemos de la fórmula adecuada que nos da la probabilidad a posteriori, estamos interesados ahora en obtener la hipótesis más probable, o hipótesis MAP (maximum a posteriori), una vez que se han observado los datos.
La expresión 2.2 la podemos escribir ahora como:
Y al ser P(D) la misma en todas las hipótesis, la obtención del máximo se calcula prescindiendo de este término:
hMAP es la hipótesis más probable, dados los datos observados, P(h/D).
En los problemas de clasificación disponemos de una variable clase (C) y un conjunto de variables predictoras o atributos que denominaremos A1, A2, …, An. Con estas especificaciones el teorema de Bayes tiene la siguiente expresión:
En los procedimientos bayesianos la hipótesis más plausible es la que tiene la máxima probabilidad a posteriori dados los atributos (hipótesis MAP), cuya expresión es la siguiente:
Donde Ωc representa el conjunto de valores que puede tomar la variable C.
En el último paso se ha eliminado el denominador, debido a que sería el mismo para todas las categorías de la variable C.
Este método sencillo y claro posee un problema que es la complejidad computacional debido a que necesitamos trabajar con distribuciones de probabilidad que involucran muchas variables, lo que en la mayoría de los casos resulta inmanejable.
2.2Clasificador Naïve BayesEl desarrollo de este famoso clasificador, incluido en la gran mayoría de paquetes informáticos, se encuentra desarrollado en Duda y Hart (1973) y en Langley et al. (1992).
Este método parte de la suposición de que todos los atributos son independientes conocido el valor de la variable clase. Este supuesto es poco realista en la mayoría de los casos, pero aun así, en muchos casos es uno de los más competitivos comparado con otras técnicas, como las redes neuronales o los árboles de clasificación (fig. 1).
La estimación de los parámetros en este método —es decir, la clase o valor a devolver— será la resultante de aplicar la siguiente fórmula:
Dados los datos de entrenamiento, se recorren todos esos datos y se computa la clasificación de cada uno de ellos, obteniendo P(Cj) para cada clasificación posible.
Cuando los atributos son discretos, la estimación de la probabilidad condicional se extrae de la base de datos, ya que son las frecuencias de aparición. Si n(xi,Pa(xi)) representa al número de registros de nuestra base de datos en el que la variable Xi toma el valor xi y a los padres de Xi lo denotamos por Pa(xi), entonces la fórmula de la probabilidad condicional viene determinada por el cociente entre el número de casos favorables y el de casos posibles:
Cuando las muestras son pequeñas o si se realizan muestreos en los que los cruces de dimensiones son frecuentes, es muy probable que los resultados obtenidos sean muy dudosos. Para atenuar este problema existen procedimientos de estimadores basados en suavizados. Uno de los más conocidos es el estimador basado en la sucesión de Laplace, que viene definido por la siguiente fórmula:
Ahora la estimación de la probabilidad viene expresada por el número de casos favorables+1 dividida por el de casos totales más el número de posibilidades o alternativas.
Esta estimación asume una distribución a priori uniforme y no puede ajustarse a nuestras necesidades si es que queremos suavizar más o menos la probabilidad. Existe otra forma de resolver el cálculo de la probabilidad: a través del m-estimador, que no es más que una generalización de la corrección de Laplace. Su expresión matemática viene representada por:
Ahora el numerador son los casos favorables más una constante m multiplicada por la frecuencia de aparición a priori del evento, y el denominador es el número de casos totales más la constante m.
Cuando los datos son continuos, el estimador Naïve Bayes supone que la distribución de esta variable continua sigue una distribución normal. La media aritmética y la desviación típica que caracterizan a esta distribución gaussiana se estiman a través de los datos muestrales.
3Redes bayesianasLas redes bayesianas se conocen en la literatura existente con otros nombres, como redes causales o redes causales probabilísticas, redes de creencia, sistemas probabilísticos, sistemas expertos bayesianos, o también como diagramas de influencia. Las redes bayesianas son métodos estadísticos que representan la incertidumbre a través de las relaciones de independencia condicional que se establecen entre ellas (Edwards, 1998). Este tipo de redes codifica la incertidumbre asociada a cada variable por medio de probabilidades. Kadie et al. (2001) afirman que una red bayesiana es un conjunto de variables, una estructura gráfica conectada a estas variables y un conjunto de distribuciones de probabilidad.
Estas redes probabilísticas automatizan el proceso de modelización probabilístico utilizando toda la expresividad de los grafos para representar las dependencias y la teoría de la probabilidad para cuantificar esas relaciones. En esta unión se realiza de forma eficiente el aprendizaje automático, como la inferencia con los datos y la información disponible
Una red bayesiana queda especificada formalmente por una dupla B=(G,Θ), donde G es un grafo dirigido acíclico (GDA) y Θ es el conjunto de distribuciones de probabilidad. Definimos un grafo como un par G=(V,E), donde V es un conjunto finito de vértices nodos o variables y E es un subconjunto del producto cartesiano V×V de pares ordenados de nodos que llamamos enlaces o aristas (fig. 2).
El grafo es dirigido y acíclico. Dirigido porque los enlaces entre los vértices de la estructura están orientados; por ejemplo, si (A, B)E pero (B,A) no E diremos que hay un enlace o un arco entre los nodos y lo representamos como A→B. Cuando se dice que es acíclico es porque no pueden existir ciclos o bucles en el grafo, lo que significa que si empezamos a recorrer un camino desde un nodo no se puede regresar al punto de partida.
Las conexiones del tipo A→B indican dependencia o relevancia directa entre las variables; en este caso se indica que B depende de A o que A es la causa de B y B es el efecto de A. También se dice que A es el padre y B el hijo. La ausencia de arcos entre los nodos nos está aportando una valiosa información, ya que en este caso el grafo nos informa de independencia condicional.
La redes bayesianas tienen la habilidad de codificar la causalidad entre las variables, por lo que han sido muy utilizadas en el modelado o en la búsqueda automática de estructuras causales (López et al., 2006). La potencia de las redes bayesianas está en su capacidad de codificar las dependencias/independencias relevantes considerando no solo las dependencias marginales sino también las dependencias condicionales entre conjuntos de variables.
La mayoría de los autores afirman que las redes bayesianas tienen 2 dimensiones: una cuantitativa y otra cualitativa (Cowell et al., 1999; Garbolino y Taroni, 2002; Nadkarni y Shenoy, 2001, 2004; Martínez y Rodríguez, 2003).
Los grafos definen un modelo probabilístico con las mismas dependencias utilizando una factorización mediante el producto de varias funciones de probabilidad condicionada:
padres(xi) son las variables predecesoras inmediatas de la variable xi en la red, precisamente p(xipadres(xi)) son los valores que se almacenan en el nodo que precede a la variable xi
A través de la factorización, las independencias del grafo son traducidas al modelo probabilístico de forma muy práctica.
Las redes bayesianas representan el conocimiento cualitativo del modelo mediante el grafo dirigido acíclico. Esta representación del conocimiento está articulada en la definición de la relaciones de dependencia/independencia. Utilizar la representación gráfica a través del grafo hace que las redes bayesianas sean una herramienta muy poderosa y atractiva como representación del conocimiento.
Estas redes bayesianas no solo modelan cualitativamente las relaciones, sino que también cuantifican y expresan de forma numérica la fuerza existente entre las variables. Existen 3 elementos que caracterizan la dimensión cuantitativa de la red bayesiana: a)el concepto de probabilidad, como medida del grado de creencia subjetiva relativa a un evento; b)un conjunto de funciones de probabilidad condicionada que definen a cada variable en el modelo, y c)el teorema de Bayes, que se utiliza para actualizar las probabilidades con base a la experiencia.
La fuerza de las relaciones entre las variables está especificada en las distribuciones de probabilidad como una medida de la creencia que tenemos sobre esas relaciones en el modelo.
Los diferentes tipos de redes bayesianas vienen determinadas por el carácter discreto o continuo de la variables involucradas en el modelo.
Cuando las variables siguen una distribución normal multivariante N(μ,Σ) decimos que la red es gaussiana, y entonces la función de densidad conjunta viene determinada por la siguiente expresión:
donde μ es el vector de medias n-dimensional, ∑ es la matriz de covarianzas n×n, |∑| es el determinante de ∑ y μT denota la traspuesta de μ.
Otro tipo de red son las multinomiales, donde se considera que todas las variables son discretas, lo que implica que todas las variables tienen un número finito de posibles estados. También suponemos que las funciones de probabilidad de cada variable condicionada a sus predecesores (padres) son también multinomiales y, por lo tanto, están especificadas en las diferentes combinaciones de estado de las variables involucradas. La reducción de parámetros a estimar es considerable.
Las redes bayesianas mixtas son muy complicadas de definir, aunque se han estudiado casos particulares. En Jordan (1998) se describe un ejemplo en el que se permite que una variable continua tenga padres con valores discretos. Otra aplicación la encontramos en Castillo et al. (1998), que describen un caso utilizando variables discretas y funciones beta.
3.1Algoritmos de aprendizaje automáticoSe ha comentado que para obtener una red bayesiana se ha de especificar una estructura gráfica y una función de probabilidad conjunta que viene especificada por el producto de la probabilidades de cada nodo dados sus padres, lo que implica que en la mayoría de las ocasiones no se conocen ni la estructura ni las probabilidades. Esta es la razón por la que se han desarrollado diferentes métodos de aprendizaje para obtener la red bayesiana conocidos los datos.
Las tareas de aprendizaje a las que se enfrentan los diferentes métodos se pueden dividir en un aprendizaje estructural y un aprendizaje paramétrico.
En el aprendizaje estructural es donde se establecen las relaciones de dependencia que existen entre las variables del conjunto de datos para obtener el mejor grafo que represente estas relaciones. Este problema, como ya se ha afirmado anteriormente, es bastante complejo, dado que la búsqueda de la estructura que nos represente mejor a los datos es un problema NP-completo, lo que lo hace computacionalmente intratable cuando el número de variables es grande. Muchas veces se buscan algoritmos eficientes que, si bien no son óptimos, sí se aproximan a la solución buscada con costes computacionales acotados (Neapolitan, 2003).
Básicamente, los métodos de aprendizaje de la estructura se pueden englobar en 2 tipos. Se encuentran, por una parte, los métodos que utilizan métricas de complejidad-bondad de ajuste y algoritmos de búsqueda. La métrica define la calidad de la red bayesiana en función de los datos y el algoritmo de búsqueda tratará de buscar la red que maximice esa métrica explorando todas las posibilidades. Hay que tener en cuenta que el número de posibles estructuras gráficas aumenta considerablemente con el número de variables. Dependiendo de la métrica utilizada y de la técnica de búsqueda existe una amplia gama de procedimientos que pueden ir desde métodos voraces simples (Cooper y Herskovitz, 1992) hasta métodos que utilizan algoritmos genéticos (Larrañaga et al., 1996).
Otros métodos están basados en test estadísticos para detectar las posibles dependencias/independencias presentes en los datos, por lo que la red se ajustaría a estas dependencias descubiertas. Estos métodos parecen más eficientes pero pueden ser muy sensibles a los fallos en los test, especialmente cuando en el problema están involucradas muchas variables (Friedman et al., 1999).
También se pueden utilizar ambas estrategias para optimizar la búsqueda y construir el grafo (Campos, 2006).
En este trabajo se han utilizado los algoritmos de búsqueda K2, TAN y el HC (Hill Climbing). El algoritmo K2 está basado en la búsqueda y optimización de una métrica bayesiana y está considerado como el predecesor y fuente de inspiración para las generaciones posteriores. El algoritmo K2 realiza una búsqueda voraz muy eficaz para encontrar una red de calidad en un tiempo razonable (Cooper y Herskovitz, 1992). El algoritmo de ascensión de colinas es un algoritmo de subida por el máximo gradiente que está basado en la definición de una vecindad.
El algoritmo TAN (del inglés Tree Augmented Network) fue propuesto en 1997 por Friedman et al. (1997). Este algoritmo consistió en una adaptación del algoritmo que propusieron Chow y Liu en 1968. El TAN utiliza el concepto de cantidad de información mutua condicionada a la variable clase, en lugar de la cantidad de información mutua en la que se basa el algoritmo de Chow y Liu (1968).
Dadas las variables discretas X e Y y la clase C, la cantidad de información que la variable Y nos proporciona sobre la variable X dada la variable clase es calculada a través de la siguiente expresión:
Cuando se aprende la estructura del árbol entre todos los atributos, el algoritmo TAN añade la variable clase y la hace padre de todas las variables.
Friedman et al. (1997) demuestran que si el contexto en el cual los datos de entrenamiento hubieran sido generados por una estructura TAN, el algoritmo visto anteriormente es asintóticamente correcto, lo que significa que si la muestra es suficientemente grande el algoritmo recuperará la estructura que generó los datos.
También se asegura que la estructura de red obtenida contiene la máxima verosimilitud del conjunto de todas las posibles estructuras TAN (Hernández Orallo et al., 2004). Por otra parte, la complejidad de este algoritmo es O(n2·N), siendo n el número de atributos y N el tamaño del conjunto de entrenamiento.
Keogh y Pazzani (1999) proponen un algoritmo voraz que aplica a una estructura Naïve Bayes. En cada uno de los pasos se añade un arco que mejore en mayor medida el porcentaje de instancias bien clasificadas, manteniendo la condición de que en la estructura final cada variable no tenga más de un padre.
Una vez conocida la estructura de la red bayesiana, el problema de la estimación de los parámetros de la red se reduce a calcular la función de probabilidad a posteriori p(ϑG/D, Gh), donde D representa el conjunto de datos de entrenamiento. Los parámetros consisten en las probabilidades a priori de los nodos raíz y las probabilidades condicionales de las demás variables, dados sus nodos padres.
La estimación de parámetros de la red bayesiana se encuentra en bastantes documentos, algunos de los más importantes son: Spiegelhalter y Lauritzen (1990), Buntine (1991) y Heckerman (1996)
4Balanceo de las clases y selección de variablesEl conjunto de datos estudiado contiene 1.767 registros que representan a los clientes de una caja de ahorros de La Rioja que demandaron un crédito. Del total de los casos, 1.565 devuelven el crédito, frente a los 167 que no reingresan el crédito. Existen 19 atributos tanto numéricos como nominales aportados por el banco. Los atributos de cada cliente nos informan sobre diversas cuestiones: estado civil, sexo, edad, tipo de trabajo, código de profesión, situación de la vivienda, nacionalidad, etcétera, así como otra información relacionada con el crédito: finalidad, importe solicitado, importes pendientes en su entidad bancaria y en otras, patrimonio, valor neto de la vivienda, situación de ingresos, cuotas y gastos de alquiler y préstamos, etcétera. También sabemos si el crédito se ha concedido o se ha denegado.
Antes de aplicar los diferentes métodos hemos de resolver 2 cuestiones fundamentales que se abordan a continuación: balanceo de la variable clase y ver cuál es el conjunto de variables explicativas óptimo para la clasificación.
4.1Balanceo de las clasesA la hora de aplicar los métodos de clasificación hemos de tener en cuenta cómo están distribuidas las instancias respecto a la clase. Al no estar balanceadas las clases, los clasificadores estarán sesgados a predecir un porcentaje más elevado de la clase más favorecida.
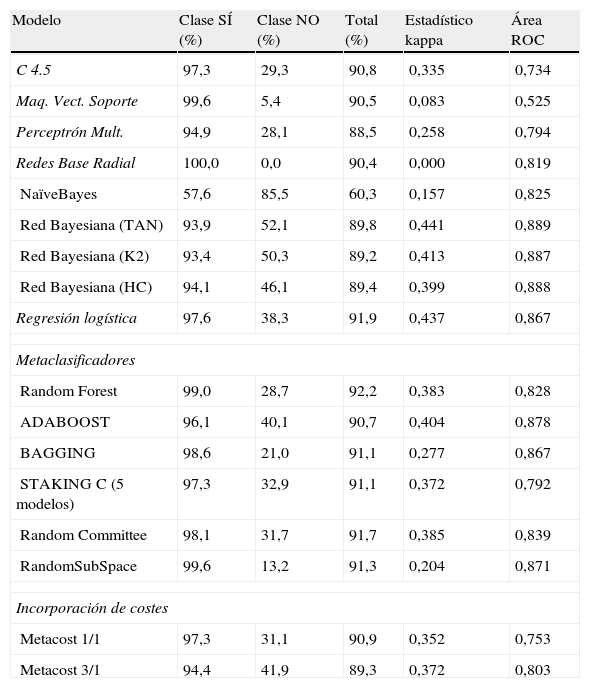
Para observar el efecto que se produce en el porcentaje de acierto, según la clase, en las tablas 1 y 2 se presenta, para diversos métodos de clasificación, el porcentaje correctamente clasificado tanto para el total como para cada una de las clases.
Muestra desbalanceada (1.565 instancias clase SI y 167 clase NO)
| Modelo | Clase SÍ (%) | Clase NO (%) | Total (%) | Estadístico kappa | Área ROC |
| C 4.5 | 97,3 | 29,3 | 90,8 | 0,335 | 0,734 |
| Maq. Vect. Soporte | 99,6 | 5,4 | 90,5 | 0,083 | 0,525 |
| Perceptrón Mult. | 94,9 | 28,1 | 88,5 | 0,258 | 0,794 |
| Redes Base Radial | 100,0 | 0,0 | 90,4 | 0,000 | 0,819 |
| NaïveBayes | 57,6 | 85,5 | 60,3 | 0,157 | 0,825 |
| Red Bayesiana (TAN) | 93,9 | 52,1 | 89,8 | 0,441 | 0,889 |
| Red Bayesiana (K2) | 93,4 | 50,3 | 89,2 | 0,413 | 0,887 |
| Red Bayesiana (HC) | 94,1 | 46,1 | 89,4 | 0,399 | 0,888 |
| Regresión logística | 97,6 | 38,3 | 91,9 | 0,437 | 0,867 |
| Metaclasificadores | |||||
| Random Forest | 99,0 | 28,7 | 92,2 | 0,383 | 0,828 |
| ADABOOST | 96,1 | 40,1 | 90,7 | 0,404 | 0,878 |
| BAGGING | 98,6 | 21,0 | 91,1 | 0,277 | 0,867 |
| STAKING C (5 modelos) | 97,3 | 32,9 | 91,1 | 0,372 | 0,792 |
| Random Committee | 98,1 | 31,7 | 91,7 | 0,385 | 0,839 |
| RandomSubSpace | 99,6 | 13,2 | 91,3 | 0,204 | 0,871 |
| Incorporación de costes | |||||
| Metacost 1/1 | 97,3 | 31,1 | 90,9 | 0,352 | 0,753 |
| Metacost 3/1 | 94,4 | 41,9 | 89,3 | 0,372 | 0,803 |
Muestra equilibrada (167 ejemplos para cada clase)
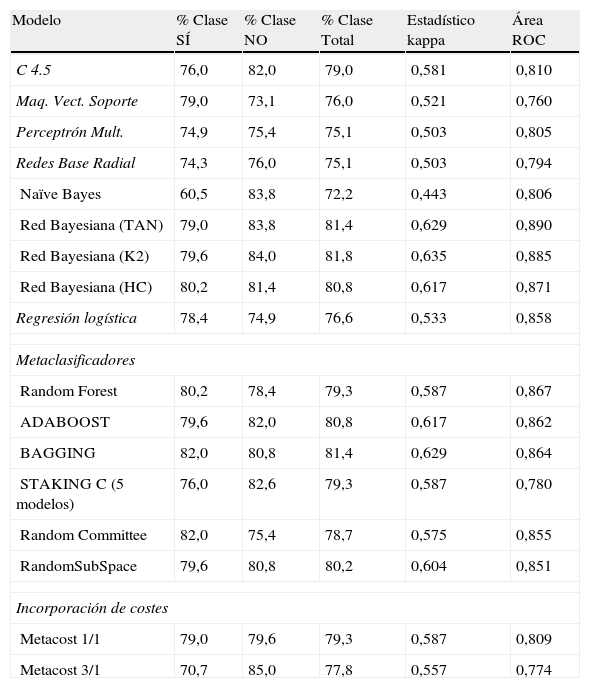
| Modelo | % Clase SÍ | % Clase NO | % Clase Total | Estadístico kappa | Área ROC |
| C 4.5 | 76,0 | 82,0 | 79,0 | 0,581 | 0,810 |
| Maq. Vect. Soporte | 79,0 | 73,1 | 76,0 | 0,521 | 0,760 |
| Perceptrón Mult. | 74,9 | 75,4 | 75,1 | 0,503 | 0,805 |
| Redes Base Radial | 74,3 | 76,0 | 75,1 | 0,503 | 0,794 |
| Naïve Bayes | 60,5 | 83,8 | 72,2 | 0,443 | 0,806 |
| Red Bayesiana (TAN) | 79,0 | 83,8 | 81,4 | 0,629 | 0,890 |
| Red Bayesiana (K2) | 79,6 | 84,0 | 81,8 | 0,635 | 0,885 |
| Red Bayesiana (HC) | 80,2 | 81,4 | 80,8 | 0,617 | 0,871 |
| Regresión logística | 78,4 | 74,9 | 76,6 | 0,533 | 0,858 |
| Metaclasificadores | |||||
| Random Forest | 80,2 | 78,4 | 79,3 | 0,587 | 0,867 |
| ADABOOST | 79,6 | 82,0 | 80,8 | 0,617 | 0,862 |
| BAGGING | 82,0 | 80,8 | 81,4 | 0,629 | 0,864 |
| STAKING C (5 modelos) | 76,0 | 82,6 | 79,3 | 0,587 | 0,780 |
| Random Committee | 82,0 | 75,4 | 78,7 | 0,575 | 0,855 |
| RandomSubSpace | 79,6 | 80,8 | 80,2 | 0,604 | 0,851 |
| Incorporación de costes | |||||
| Metacost 1/1 | 79,0 | 79,6 | 79,3 | 0,587 | 0,809 |
| Metacost 3/1 | 70,7 | 85,0 | 77,8 | 0,557 | 0,774 |
El tamaño de la muestra juega un papel determinante en la bondad de los modelos de clasificación. Cuando el desbalanceo es considerable, descubrir regularidades inherentes a la clase minoritaria se convierte en una tarea ardua y de poca fiabilidad. Japkowicz y Stephen (2002) concluyen que si los dominios son separables linealmente, los modelos no son sensibles al problema del desequilibrio de las clases.
En el ejemplo que estamos tratando podemos ver que cuando mantenemos la base de datos con las clases desequilibradas todos los métodos presentan una importante diferencia de aciertos entre las clases.
Los métodos de clasificación favorecen en general a la clase mayoritaria salvo en el caso del clasificador bayesiano Naïves Bayes, que clasifica mejor a la clase minoritaria. Se da el caso extremo en el que un clasificador, las máquinas de vectores soporte, clasifican correctamente a todos los de la clase mayoritaria y a ninguno de la minoritaria. Tampoco los metaclasificadores estiman correctamente ambas clases. Solamente introduciendo un método cuyo aprendizaje sea sensible al coste se logra equilibrar la precisión de los ejemplos bien clasificados.
Las soluciones para tratar el desbalanceo se pueden encuadrar en 2 grupos: soluciones a nivel de datos y a nivel de algoritmos.
Las técnicas dirigidas a modificar los datos tratan de remuestrear las tallas de entrenamiento, bien sea a través del sobremuestreo de la clase minoritaria o del submuestreo de la clase que tiene mayores instancias. Aunque estas técnicas han demostrado su efectividad, no dejan de tener ciertos inconvenientes: pueden eliminar ejemplos útiles e incrementar los costes. Otra crítica a esta estrategia se refiere al cambio que se realiza en la distribución original del conjunto de entrenamiento de los datos
En el tabla 2 se expresan los resultados de diferentes clasificadores aplicados a una muestra donde se han balanceado ambas clases. La forma de extraer los registros de la clase más numerosa ha sido aleatoria. Cuando existe equilibrio de las instancias en la base de datos, los porcentajes de acierto de los clasificadores para ambas clases están mucho más igualados.
El tema de muestras desbalanceadas se ha tratado extensamente y se han utilizado muchas estrategias, aunque se puede afirmar que no existe una solución concluyente sobre qué solución es mejor. Hulse et al. (2007) concluyen que la decisión sobre la mejor técnica está influida en gran medida por la naturaleza del clasificador y la medida de efectividad.
Otra forma que disponemos para combatir el desbalance de clases es a través del establecimiento de una matriz de costes, lo que se ha llamado método del costo-sensitivo (cost-sensitive). Este método se basa en la aseveración de que el precio de cometer un error de clasificación debe ser distinto para cada clase. Es evidente que en este ejemplo no es lo mismo conceder un crédito y no pagarlo que no concederlo cuando se debería haber concedido.
En este trabajo, el clasificador que se aplica para poder comparar con el resto de los algoritmos es el metacost (Domingos, 1999). El objetivo de este procedimientos es reetiquetar cada muestra de entrenamiento por la estimación del riesgo de Bayes. Finalmente, el clasificador se entrena con un método no basado en costes con el conjunto que ya ha sido reetiquetado.
La técnica más sencilla de sobremuestreo es la aleatoria simple a través de la réplica de ejemplos en la misma clase, pero este método puede ocasionar un alto sobreajuste de los clasificadores.
Como técnica más inteligente para incrementar los ejemplos de la clase minoritaria se encuentra el ya citado algoritmo SMOTE, originario de Chawla et al. (2002). En este método la creación de nuevas muestras se origina a través de la interpolación. En un primer paso elegimos los k vecinos más cercanos y que pertenecen a su misma clase. Posteriormente elegimos el número de muestras artificiales que se generarán, y finalmente, para generar una nueva muestra se calcula la diferencia entre el vector de atributos bajo consideración y uno de los vecinos más cercanos de los k vecinos elegidos al azar. El resultado de la diferencia se multiplica por un valor aleatorio entre cero y uno.
El algoritmo SMOTE se ha modificado de diferentes maneras para adaptarse mejor a muchos ejemplos. Algunas de estas aportaciones son las efectuadas por Han et al. (2005), que proponen el algoritmo Borderline-SMOTE para generar ejemplos positivos cercanos a una frontera. Wang et al. (2006) presentan el algoritmo LLE-SMOTE (Locally Linear Embedding), que proyecta conjuntos de alta dimensionalidad a otro de menor dimensionalidad. En este espacio de reducida dimensionalidad es donde se aplica SMOTE, y después los ejemplos generados son transformados a su espacio de representación original.
Otras formas de obtener una representación mayor de la clase minoritaria se basan en técnicas de agrupamiento. Por ejemplo, Japkowicz (2001) emplea el algoritmo de clustering k-medias sobre cada clase por separado. Los clusters resultantes se sobremuestrean aleatoriamente hasta conseguir un equilibrio entre las clases. Otro trabajo en esta línea de investigación es el de Cohen et al. (2006), que también explora la generación de nuevas instancias a través de algoritmos de clustering, pero en este caso los centroides de los clusters se obtienen a través de un algoritmo aglomerativo jerárquico.
En cuanto a las técnicas de submuestreo, una de las primeras propuestas para editar o filtrar las muestras de entrenamiento fue el algoritmo de Edición de Wilson (1972), también conocido como la regla del vecino más cercano editado (Edited Nearest Neighbor). Actualmente existen muchas formas de proceder, y algunas de ellas son las siguientes: a través del submuestreo aleatorio de Jo y Japkowicz (2004) con submuestreo dirigido; el algoritmo One-sides selection de Kubat y Matwin (1997), con técnicas de vecindad; el algoritmo Neighbordhood Cleaning Rule de Laurikkala (2002) con submuestreo aplicando algoritmos genéticos (Kuncheva y Jain, 1999), con submuestreo por distancia (Zhang y Mani, 2003), con submuestreo por clustering (Cohen et al., 2006) y a través del aprendizaje activo de Provost (2003). Respecto a los métodos de clasificación en entornos no balanceados que no cambian la distribución a priori de las clases, nos encontramos con las soluciones a nivel de algoritmos: aprendizaje sensible al coste, algoritmos de clasificación con sesgo hacia la clase minoritaria y los clasificadores de una clase.
En esta investigación los resultados de los diferentes clasificadores que se presentan se aplican a un conjunto de datos que se han balanceado a través de un método mixto donde se aplica el método SMOTE a la clase minoritaria y se reduce la muestra de la clase mayoritaria a través del método del submuestreo equilibrado del cubo, propuesto por Deville y Tillé, 2004. Este método de muestreo es el único que nos permite seleccionar una muestra equilibrada sobre variables auxiliares con probabilidades de inclusión iguales o no. El método del cubo selecciona únicamente las muestras cuyos estimadores de Horvitz-Thompson son iguales a los totales de las variables auxiliares conocidas.
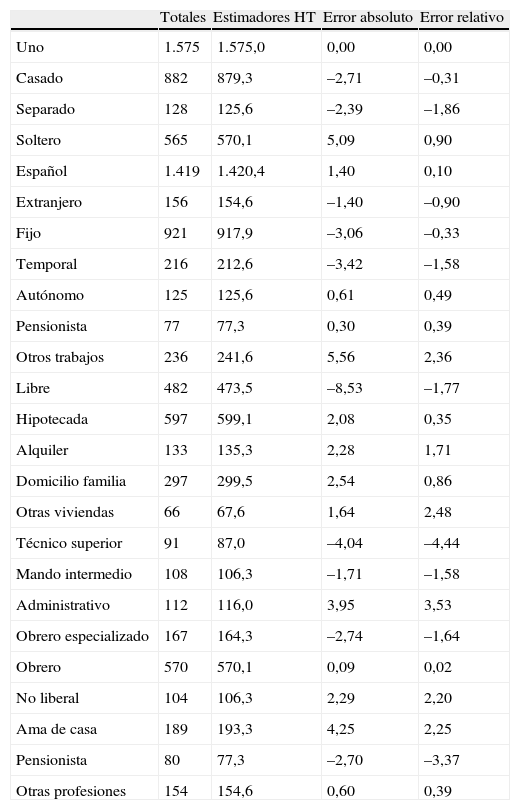
De los 1.575 ejemplos disponibles que devolvieron el crédito se han seleccionado 312 registros a través del método del cubo. Para esta selección de los individuos las variables auxiliares utilizadas por el método del cubo han sido el estado civil, la nacionalidad, el tipo de trabajo, las condiciones de la casa y el tipo de trabajo de las personas que solicitan el crédito. El número de muestras que ha considerado este método para llegar a la solución más idónea ha sido de 77.250 muestras. En la tabla 3 se presentan, para la muestra elegida, los totales y los estimadores de Horvitz-Thompson (que dependen de la muestra), así como los errores absolutos y relativos, en porcentaje, entre ambos para cada variable de equilibrio.
Resultados del submuestreo equilibrado. Método del cubo
| Totales | Estimadores HT | Error absoluto | Error relativo | |
| Uno | 1.575 | 1.575,0 | 0,00 | 0,00 |
| Casado | 882 | 879,3 | –2,71 | –0,31 |
| Separado | 128 | 125,6 | –2,39 | –1,86 |
| Soltero | 565 | 570,1 | 5,09 | 0,90 |
| Español | 1.419 | 1.420,4 | 1,40 | 0,10 |
| Extranjero | 156 | 154,6 | –1,40 | –0,90 |
| Fijo | 921 | 917,9 | –3,06 | –0,33 |
| Temporal | 216 | 212,6 | –3,42 | –1,58 |
| Autónomo | 125 | 125,6 | 0,61 | 0,49 |
| Pensionista | 77 | 77,3 | 0,30 | 0,39 |
| Otros trabajos | 236 | 241,6 | 5,56 | 2,36 |
| Libre | 482 | 473,5 | –8,53 | –1,77 |
| Hipotecada | 597 | 599,1 | 2,08 | 0,35 |
| Alquiler | 133 | 135,3 | 2,28 | 1,71 |
| Domicilio familia | 297 | 299,5 | 2,54 | 0,86 |
| Otras viviendas | 66 | 67,6 | 1,64 | 2,48 |
| Técnico superior | 91 | 87,0 | –4,04 | –4,44 |
| Mando intermedio | 108 | 106,3 | –1,71 | –1,58 |
| Administrativo | 112 | 116,0 | 3,95 | 3,53 |
| Obrero especializado | 167 | 164,3 | –2,74 | –1,64 |
| Obrero | 570 | 570,1 | 0,09 | 0,02 |
| No liberal | 104 | 106,3 | 2,29 | 2,20 |
| Ama de casa | 189 | 193,3 | 4,25 | 2,25 |
| Pensionista | 80 | 77,3 | –2,70 | –3,37 |
| Otras profesiones | 154 | 154,6 | 0,60 | 0,39 |
El alto número de variables recogidas para el estudio de un fenómeno a veces es un problema para el aprendizaje si el número de instancias o ejemplos de la muestra es reducido. Este es el problema conocido como la maldición de la multidimensionalidad.
Aunque, como se verá más adelante, la solución escogida se realiza a través de la envolvente de Markov, en la literatura de selección de variables existen 2 métodos generales para escoger las mejores características de la base de datos: métodos de filtro y métodos basados en modelos. En los primeros se filtran los atributos irrelevantes antes de aplicar las técnicas de minería de datos. El criterio que establece las variables óptimas se basa en una medida de calidad que se calcula a partir de los datos mismos. En los métodos basados en modelos, también conocidos como métodos de envolvente o wrapper, la bondad de la selección de las variables se evalúa a través de un modelo utilizando, lógicamente, un método de validación.
En el caso de la selección de atributos debemos definir un algoritmo que evaluará cada atributo individualmente del conjunto de datos inicial, que se denomina «attribute evaluator», y un método de búsqueda que hará una búsqueda en el espacio de posibles combinaciones de todos los subconjuntos del conjunto de atributos.
De esta forma podremos evaluar independientemente cada una de las combinaciones de atributos y, con ello, seleccionar las configuraciones de atributos que maximicen la función de evaluación de atributos.
Para resolver el problema de plantear combinaciones de atributos o la función que evalúa cada subconjunto de atributo es preciso utilizar un algoritmo de búsqueda que recorra el espacio de posibles combinaciones de una forma organizada, o adecuada al problema.
Además del método de las componentes principales, existen 2 tipos de evaluadores: evaluadores de subconjuntos o selectores (SubSetVal) y prorrateadores de atributos (AttributeEval).
Los SubSetVal necesitan una estrategia de búsqueda (Search Method) y los AttributeEval ordenan las variables según su relevancia, así que necesitan un Ranker.
Habitualmente, en las situaciones en la que se emplea selección de atributos no es posible hacer un recorrido exhaustivo en el espacio de combinaciones, por lo que la selección adecuada de un algoritmo de búsqueda resulta crítica.
Para esta base de datos se utiliza, en primer lugar, el algoritmo evaluador de atributos «CfsSubsetEval», del que disponen ya muchos programas. Este algoritmo es el más sencillo, ya que puntúa a cada atributo en función de su entropía. Como algoritmo de búsqueda utilizamos los algoritmos genéticos. En segundo lugar recurrimos al método Ranker para que nos facilite una ordenación de los atributos según su importancia.
Los algoritmos genéticos propuestos por Holland (1975) suponen uno de los enfoques más originales en la minería de datos. Se inspiran en el comportamiento natural de la evolución, y para ello se codifica cada uno de los casos de prueba como una cadena binaria (que se asemejaría a un gen). Esta cadena se replica o se inhibe en función de su importancia, determinada por una función denominada de ajuste o fitness.
Los algoritmos genéticos son adecuados para obtener buenas aproximaciones en problemas de búsqueda, aprendizaje y optimización (Marczyk, 2004).
La solución que nos parece más óptima y adecuada a este problema en cuanto al número de variables utilizadas en la aplicación de los modelos y algoritmos de clasificación es seleccionar los atributos para la clasificación a través de los resultados observados en el manto de Markov.
La envolvente de Markov para una variable representa el conjunto de variables de las que depende dicha variable. Así, si aplicamos la envolvente o manto de Markov a esta red bayesiana, definida esta envolvente como:
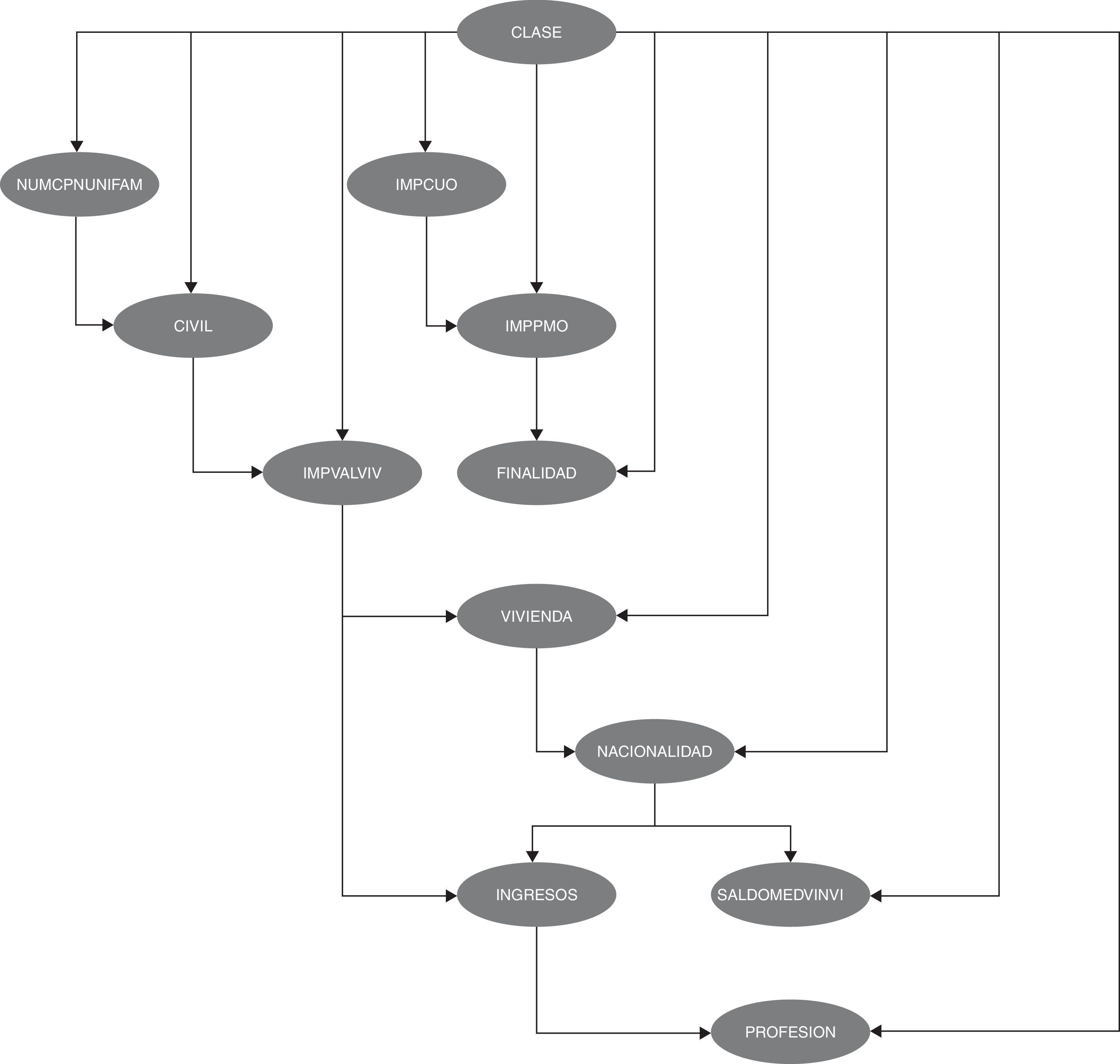
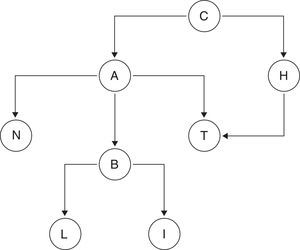
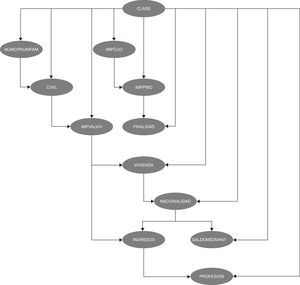
obtenemos que las 19 variables originales se han reducido a 11, dado que 8 de ellas no contienen información relevante conocidas el resto de variables. El grafo que muestra la estructura de dependencias/independencias es el de la figura 3.
Esta figura se ha obtenido utilizando el algoritmo HC, que parte de una red de enlaces vacía y emplea una métrica BIC (Bayesian Information Criterion) como método de aprendizaje.
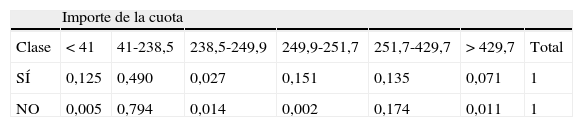
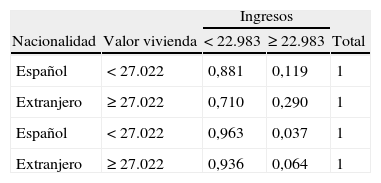
En esta red se pueden observar las relaciones de dependencia directas e indirectas entre las variables. Entre estas dependencias podemos destacar, entre otras, la relación entre la cuota del crédito (IMPCUO), el importe (IMPPMO) y la finalidad a la que se destina (FINALIDAD). Otra relación interesante es la que se observa entre la nacionalidad, los ingresos y la profesión, y entre la nacionalidad y el saldo medio no vista.
A esta estructura de relaciones entre las variables hay que añadir que todos los nodos tienen una probabilidad asignada, al igual que una probabilidad condicionada a los valores del cual dependen sus padres. Es esta estructura de probabilidades, junto con la capacidad descriptiva de la red, la que dota a los métodos bayesianos de una mayor eficacia, potencia y versatilidad respecto a otros métodos no probabilísticos. Véase Como ejemplo de las múltiples posibilidades que se ofrecen, véanse 2 tablas de probabilidades asociadas a las relaciones entre las variables de las cuales dependen (tablas 4 y 5).
El proceso de discretización de las variables cuantitativas necesarias para la estimación de la red bayesiana se ha realizado a través del método de la mínima entropía propuesto por Fayyard y Irani (1993). En este método se seleccionan los puntos de corte de forma recursiva mediante un algoritmo de minimización de la entropía usando el criterio de «longitud de descripción mínima» propuesto por Suzuki (1996).
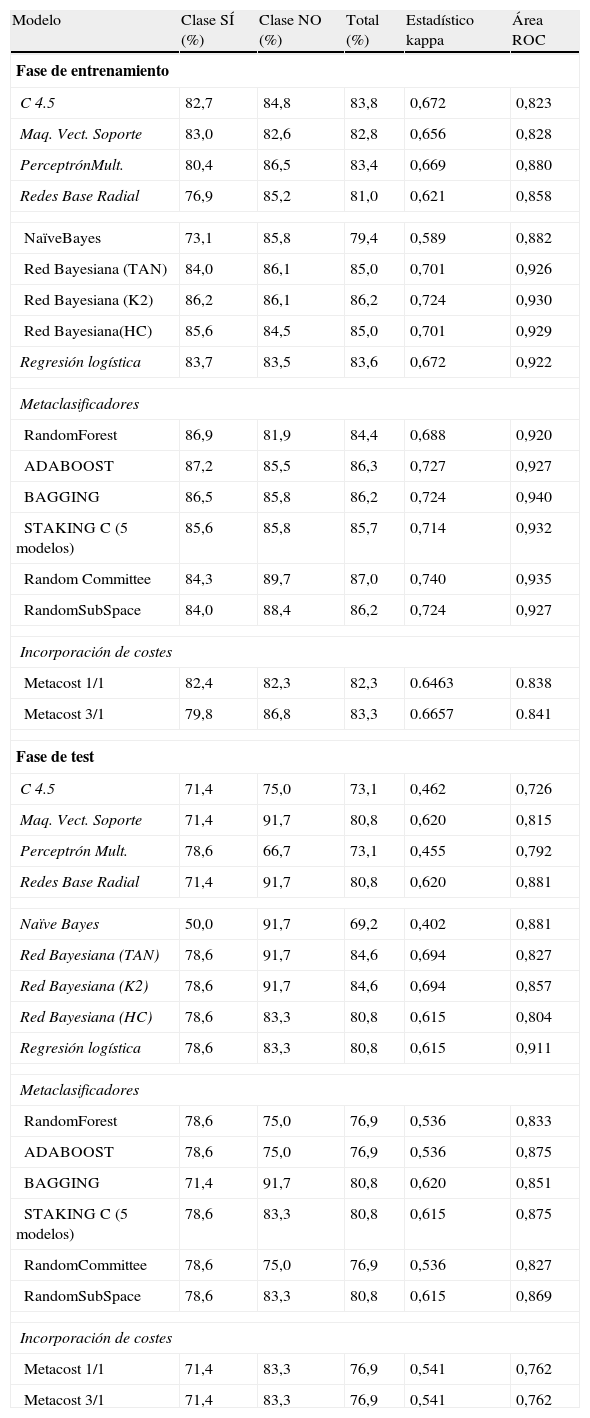
5Resultados obtenidos. Comparación de clasificadoresLos resultados que se ofrecen en este epígrafe se resumen en la tabla 6, donde se detallan los resultados para el conjunto de datos con 11 variables que se seleccionan al aplicar los resultados observados en el manto de Markov. En todas las predicciones que arrojan los modelos utilizados se muestran el porcentaje total de aciertos, desglosados para ambas clases, y las medidas de evaluación de los 16 modelos que se han utilizado.
Resultados con SMOTE y método del cubo
| Modelo | Clase SÍ (%) | Clase NO (%) | Total (%) | Estadístico kappa | Área ROC |
| Fase de entrenamiento | |||||
| C 4.5 | 82,7 | 84,8 | 83,8 | 0,672 | 0,823 |
| Maq. Vect. Soporte | 83,0 | 82,6 | 82,8 | 0,656 | 0,828 |
| PerceptrónMult. | 80,4 | 86,5 | 83,4 | 0,669 | 0,880 |
| Redes Base Radial | 76,9 | 85,2 | 81,0 | 0,621 | 0,858 |
| NaïveBayes | 73,1 | 85,8 | 79,4 | 0,589 | 0,882 |
| Red Bayesiana (TAN) | 84,0 | 86,1 | 85,0 | 0,701 | 0,926 |
| Red Bayesiana (K2) | 86,2 | 86,1 | 86,2 | 0,724 | 0,930 |
| Red Bayesiana(HC) | 85,6 | 84,5 | 85,0 | 0,701 | 0,929 |
| Regresión logística | 83,7 | 83,5 | 83,6 | 0,672 | 0,922 |
| Metaclasificadores | |||||
| RandomForest | 86,9 | 81,9 | 84,4 | 0,688 | 0,920 |
| ADABOOST | 87,2 | 85,5 | 86,3 | 0,727 | 0,927 |
| BAGGING | 86,5 | 85,8 | 86,2 | 0,724 | 0,940 |
| STAKING C (5 modelos) | 85,6 | 85,8 | 85,7 | 0,714 | 0,932 |
| Random Committee | 84,3 | 89,7 | 87,0 | 0,740 | 0,935 |
| RandomSubSpace | 84,0 | 88,4 | 86,2 | 0,724 | 0,927 |
| Incorporación de costes | |||||
| Metacost 1/1 | 82,4 | 82,3 | 82,3 | 0.6463 | 0.838 |
| Metacost 3/1 | 79,8 | 86,8 | 83,3 | 0.6657 | 0.841 |
| Fase de test | |||||
| C 4.5 | 71,4 | 75,0 | 73,1 | 0,462 | 0,726 |
| Maq. Vect. Soporte | 71,4 | 91,7 | 80,8 | 0,620 | 0,815 |
| Perceptrón Mult. | 78,6 | 66,7 | 73,1 | 0,455 | 0,792 |
| Redes Base Radial | 71,4 | 91,7 | 80,8 | 0,620 | 0,881 |
| Naïve Bayes | 50,0 | 91,7 | 69,2 | 0,402 | 0,881 |
| Red Bayesiana (TAN) | 78,6 | 91,7 | 84,6 | 0,694 | 0,827 |
| Red Bayesiana (K2) | 78,6 | 91,7 | 84,6 | 0,694 | 0,857 |
| Red Bayesiana (HC) | 78,6 | 83,3 | 80,8 | 0,615 | 0,804 |
| Regresión logística | 78,6 | 83,3 | 80,8 | 0,615 | 0,911 |
| Metaclasificadores | |||||
| RandomForest | 78,6 | 75,0 | 76,9 | 0,536 | 0,833 |
| ADABOOST | 78,6 | 75,0 | 76,9 | 0,536 | 0,875 |
| BAGGING | 71,4 | 91,7 | 80,8 | 0,620 | 0,851 |
| STAKING C (5 modelos) | 78,6 | 83,3 | 80,8 | 0,615 | 0,875 |
| RandomCommittee | 78,6 | 75,0 | 76,9 | 0,536 | 0,827 |
| RandomSubSpace | 78,6 | 83,3 | 80,8 | 0,615 | 0,869 |
| Incorporación de costes | |||||
| Metacost 1/1 | 71,4 | 83,3 | 76,9 | 0,541 | 0,762 |
| Metacost 3/1 | 71,4 | 83,3 | 76,9 | 0,541 | 0,762 |
Las instancias utilizadas han sido extraídas aplicando a la base de datos original el método del cubo a la clase dominante y el método de sobremuestreo denominado SMOTE a la clase minoritaria, descritos brevemente en las páginas anteriores. Al aplicar estos 2 procedimientos se obtiene una base de datos que contiene 312 individuos de la clase SÍ (devuelven el crédito) y 310 de la clase NO (no pagan el crédito).
Los métodos empleados en la clasificación son los siguientes: regresión logística, máquinas de vectores soporte, 2 modelos de redes neuronales, el C.4.5 como árbol de clasificación, 6 métodos multiclasificadores y el algoritmo Metacost con y sin matrix de costes. Los resultados de todos los modelos son comparados con los que se obtienen a través de los métodos estadísticos bayesianos explicados anteriormente. En concreto, se han aplicado 3 redes bayesianas que buscan y optimizan la métrica bayesiana a través de los algoritmos K2, HC (Hill Climbing) y TAN (Tree Augmented Naïve Bayes).
El multiclasificador Stacking se configura con 5 modelos: perceptrón multicapa, red bayesiana con el algoritmo de búsqueda K2, regresión logística, máquinas de vectores soporte y el árbol de clasificación, C4.5.
En la tabla 3 se presentan los resultados de todos los modelos estudiados con 15 variables tanto en la fase de entrenamiento como en la fase de test, realizada esta con 26 registros seleccionados aleatoriamente de la base de datos.
Como cuestión más destacada podemos afirmar que 2 de los 3 modelos de redes bayesianas alcanzan, en la fase de test, los mejores resultados en precisión de aciertos y en los valores del estadístico kappa: TAN y K2 obtienen un porcentaje de aciertos del 84,6% y valores del estadístico kappa del 0,694. También son estos 2 modelos, junto con algunos otros, los que pronostican el mayor número de aciertos en la clase NO (no se concede el crédito). El área bajo la curva ROC es bastante elevada (0,827). La red entrenada con HC alcanza el 80,8% de registros bien clasificados y obtiene valores más bajos en los estadísticos.
Una particularidad de los modelos de redes bayesianos es que mantienen una similar precisión en el porcentaje global de valores bien pronosticados, tanto en la fase de entrenamiento como en la fase de test, cuestión que no ocurre en el resto de los modelos en esta fase, que, por otra parte, es la fase que realmente importa, dado que muchos de los métodos de minería de datos tienden a sobreajustarse a los datos en la fase de entrenamiento.
También se observa que en la fase de entrenamiento todos los modelos individuales utilizados son menos precisos que los multiclasificadores, si observamos el porcentaje de aciertos, el estadístico kappa y el área ROC. Entre estos, el que más acierta es el Random Committee (87,0%). La regresión logística también ofrece, en esta etapa, buenos resultados (83,6%), al igual que los árboles de decisión.
En la fase de test, entre los multiclasificadores, 3 de ellos presentan un 80,8% de aciertos: Stacking, Bagging y Random Subspace. Stacking, al igual que la redes bayesianas, TAN, K2 y HC, de las 12 instancias de la clase minoritaria y más importante en términos de coste, predicen correctamente 11 de ellas, o sea, el 91,7%, y respecto a la otra clase, económicamente menos importante, el método Bagging alcanza solo el 71,4% de los registros correctamente clasificados, mientras que TAN y K2 llegan al 78,6%.
6ConclusionesComo resumen del análisis de los datos y la aplicación de los modelos utilizados en este artículo podemos extraer las siguientes conclusiones:
- •
La utilización de las redes bayesianas con un óptimo equilibrado de las instancias, unido a la correcta selección del conjunto de variables explicativas para la resolución del problema del credit scoring, nos ha conducido a obtener excelentes resultados en la fase de entrenamiento y la mayor precisión en la fase de test.
- •
Además, las redes bayesianas se convierten en modelos muy óptimos dado que pueden incorporar información de los expertos en el área de estudio y optimizar aún más el porcentaje de aciertos.
- •
Cuando las bases de datos están desbalanceadas, las mejores opciones se experimentan cuando se equilibran las muestras. Por el análisis de la extensa bibliografía existente se constata que existen muchas propuestas que intentan solucionar este problema sin que aún exista la solución ideal, y que los resultados dependen de las características intrínsecas de los datos.
- •
Cuando el coste económico de la clasificación es diferente según las clases, como en el credit scoring, incorporar la matriz de costes es muy conveniente. Algunos métodos, como el Metacost, obtienen resultados muy aceptables ponderando la matriz de costes, ya que optimizan el análisis coste-beneficio.
- •
La selección de variables es una tarea imprescindible para buscar modelos más sencillos e interpretables. En este sentido, la ayuda de la envolvente de Markov ha reducido significativamente el número de variables, mejorando la interpretabilidad del modelo elegido.
- •
También podemos afirmar que, para resolver el problema del credit scoring, los métodos multiclasificadores obtienen buenos resultados y, en general, son más precisos que cuando los algoritmos son utilizados individualmente.
En 1921 se publicaron los trabajos de Keynes y Knigth (A Treatise on Probability, Cambridge University) y de Knight (Risk, Uncertainty, and Profit, Boston, MA), que distinguieron con nitidez los conceptos de riesgo, susceptible de medición al disponer de una distribución de probabilidad, y de incertidumbre, cuando no se puede asignar probabilidad a los sucesos.