El artículo examina la importancia de la utilización de experimentos durante el proceso de formación en estudiantes universitarios, así como el uso de teoría de juegos en experimentos desarrollados en un ambiente competitivo. Se propone un diseño experimental basado en el modelo teórico de Karlinger y Motta (2012). El experimento se desarrolló con 24 estudiantes de pregrado de Economía de la Escuela Superior Politécnica del Litoral (ESPOL), quienes jugaron aleatoriamente en dos escenarios distintos. Se estimó un modelo de probabilidad lineal (MPL) para comprobar que no existe un efecto marginal estadísticamente significativo del escenario experimental respecto de la decisión de compra individual, así como también de la consiguiente entrada de la empresa al mercado. Además, se encontró que determinadas características de los jugadores, como género y tener conocimiento sobre teoría de juegos, son factores relevantes.
This article examines the importance of experiments in the undergraduate learning process, as well as the use of game theory in experimental designs oriented towards competitive environments. For this purpose, an experimental design based on the theoretical model presented by Karlinger and Motta (2012) is proposed. The experiment was conducted with 24 Economics undergraduate from a polytechnic university (Escuela Superior Politécnica del Litoral). The students were organised to play randomly in two different scenarios. A linear probability model (LPM) was used to test whether there was a statistically significant effect for the experimental scenario on individual purchase decisions, as well as the subsequent entry of the company into the market. It was also found that other idiosyncratic characteristics, such as gender and knowledge of game theory, were relevant factors.
En el ámbito de la educación, un importante aporte al proceso de aprendizaje de los estudiantes es la aplicación de ejercicios académicos, ya sea como juegos o experimentos, de forma que capture la atención y promueva el interés por aprender de los mismos (Lawrence, 2004, p. 459). En la literatura se pueden encontrar distintos experimentos aplicados en el ámbito educacional que demuestran un efecto positivo de la competencia y la motivación en el desempeño académico de los estudiantes en diferentes áreas del conocimiento (Burguillo, 2010, p. 566; Ebner y Holzinger, 2007, p. 874; Hänze y Berger, 2007, pp. 29-30). Por otra parte, Holt recopila los resultados de cuatro trabajos anteriores, los mismos que consisten en diferentes experimentos desarrollados en el área de la educación (Holt, 1999, pp. 609-610). El primero de estos tuvo como finalidad que los estudiantes apliquen la teoría de oferta y demanda mediante el uso de conceptos como el de excedente del consumidor y productor (Laury y Holt, 1999, pp. 611-614). El segundo experimento sintetizado en el documento de Holt es acerca de los resultados de una elección política, donde los estudiantes logran una comprensión profunda sobre el voto estratégico y el efecto de las instituciones políticas sobre asignaciones económicas (Holt y Anderson, 1999, p. 622). La tercera investigación propone un juego de coordinación con equilibrios múltiples y aplicación de teoría de juegos. Este documento es una explicación del uso del experimento en cursos introductorios de economía, así como también en microeconomía intermedia para conceptos de teoría de juegos (Capra y Holt, 1999, pp. 630-631). El último experimento presentado es una aplicación macroeconómica en la que los estudiantes comprenden la diferencia que existe entre salarios reales y salarios nominales (Goeree y Holt, 1999, pp. 637-638).
En todos los experimentos que se sintetizaron en el documento en mención se llegaba a una conclusión en común. Existe una mayor eficacia del aprendizaje a través de distintos métodos de enseñanza, sobre todo mediante la aplicación de juegos experimentales, ya que se asimilan de mejor forma los conocimientos teóricos.
En base a la experiencia en desarrollo de experimentos, Holt presenta importantes recomendaciones a tomar en cuenta al momento de realizar diseños experimentales (Holt, 1999, p. 604). Uno de los aspectos más relevantes que recalca en su trabajo es el hecho de que no se debe confundir el manejo de experimentos de clases con diseños de investigación experimental más elaborados. También suelen presentarse algunos casos donde existe recelo por parte de los docentes en desarrollar experimentos, por la creencia de que para que los mismos se desarrollen de forma exitosa es necesario contar con incentivos monetarios importantes para los participantes. Sin embargo, se ha comprobado que incentivos no pecuniarios representan importantes estímulos para los jugadores. Otra de las recomendaciones recalcadas para desarrollar experimentos es trabajar con grupos pequeños, ya que se facilita e incentiva el interés por parte de los participantes.
Villalta et al. concluyen que la mediación tecnológica fortalece las actividades interactivas del aula asegurando operatividad, debido a que su funcionamiento incluye procesos establecidos con anterioridad que benefician la participación de los estudiantes (Villalta et al., 2015, p. 417). Además, Arroyo et al. han recalcado la importancia de tomar en cuenta las ventajas en el proceso de toma de decisión (Arroyo et al., 2015, p. 7). En este caso, al tratarse de un experimento en el que los jugadores toman decisiones de compra, se considera que el conocimiento previo sobre teoría de juegos es la principal ventaja que tienen algunos estudiantes sobre otros, de forma que esto es la base para hacer comparaciones en los resultados.
Estudios más recientes en el campo de la educación muestran resultados congruentes con lo discutido anteriormente. Burguillo propone que el uso de experimentos como base metodológica puede ser aplicado para contribuir al desarrollo de técnicas de aprendizaje en distintas áreas, como biología, ciencias sociales, ciencias computacionales, matemáticas y economía. Además, sugiere que el uso de teoría de juegos, junto con un ambiente de competencia amistosa, provee una fuerte motivación a los estudiantes, ayudándolos a mejorar su rendimiento académico (Burguillo, 2010, p. 567).
Por otro lado, Ebner y Holzinger proponen que el uso de juegos como técnica de aprendizaje en la educación superior permite que el conocimiento teórico sea más accesible para los estudiantes (Ebner y Holzinger, 2007, pp. 874-875). A partir de esto, se justifica el desarrollo de ejercicios experimentales que permitan explicar los distintos modelos de competencia imperfecta que pueden ser utilizados en clases de microeconomía garantizando el aprendizaje de la teoría.
En virtud de lo expuesto, el presente artículo resume el desarrollo de un ejercicio académico mediante el cual se propone un diseño experimental a partir del modelo elaborado por Karlinger y Motta (2012), el cual elabora un esquema de competencia imperfecta a la Bertrand con productos y costos diferenciados. Dicho modelo aborda la predicción de la entrada de una empresa nueva en un mercado para bienes con características de red y de estructura monopolística. En ocasión del evento «Día de Nash» realizado en las instalaciones de la Facultad de Ciencias Sociales y Humanísticas de la Escuela Superior Politécnica del Litoral, se desarrolló un experimento con la finalidad de evaluar el efecto que tiene estudiar teoría de juegos en las decisiones estratégicas que puedan adoptar los participantes y se contrastan las conclusiones teóricas del modelo en un ambiente académico. Para la ejecución del experimento se contó con la participación de 24 estudiantes de diferentes niveles de estudio seleccionados de manera aleatoria del grupo registrado en el evento.
El documento ha sido organizado en cuatro secciones. La siguiente sección detalla la metodología utilizada, describiendo en primer lugar el modelo teórico en el que se basa junto con otras perspectivas teóricas presentes en la literatura y, en segundo lugar, la descripción del diseño experimental desarrollado. La sección 3 detalla los procesos de recolección de datos y resultados derivados a partir del análisis empírico de los mismos. Finalmente, en la sección 4 se presentan conclusiones y recomendaciones generales del ejercicio.
2Metodología2.1Marco teóricoEl modelo presentado por Karlinger y Motta es utilizado como base teórica para el diseño experimental propuesto en este trabajo (Karlinger y Motta, 2012, pp. 78-80). Este modelo considera dos firmas, una establecida, denominada I, y otra entrante, denominada E. La firma I proporciona un bien de red y tiene una base de consumidores previamente establecida de tamaño βl>0. Dicha base de compradores podrá seguir consumiendo el bien provisto por la firma I pero no necesariamente deben comprarlo; sin embargo, una vez elegido el proveedor no es posible cambiarlo durante la misma ronda. Además, la firma I cuenta con un costo marginal cI∈−(0, 1), mientras que la firma E cuenta con un costo marginal igual a cE<cI. La firma E planifica entrar al mercado (i.e., βE=0) y no debe incurrir en costos de entrada.
El bien de red puede ser vendido a m nuevos compradores a un precio uniforme. Los compradores tienen una elasticidad precio-demanda inelástica con igual disposición de pago p¯=1. No obstante, pueden diferir en su cantidad demandada, si, de modo que s1≤s2≤...sm y se normaliza para que ∑si=1. Esto es, la cantidad demandada puede ser simétrica o asimétrica entre compradores. El tamaño de la red para k=I, E se denota como qk y está determinada por la expresión: qk=βk+s1v+...+smv, donde el exponente v toma el valor de 1 si el comprador adquiere el bien de la firma k, o 0 en caso contrario.
Por otra parte, el bien de red producido por ambas firmas es homogéneo, pero incompatible. Si el tamaño de la red de I, qI, está por debajo de un tamaño crítico q¯, entonces el consumo del bien producido por I genera una utilidad igual a 0 para sus compradores. Se asume que la firma I ha alcanzado el tamaño crítico (i.e., βI ≥ q¯) independientemente de las decisiones de compra, y que sm
A partir de allí, el juego se desempeña en la siguiente secuencia:
- •
En t=0, I y E anuncian simultáneamente sus precios pk∈0,1, que serán aplicados en t=1.
- •
En t=1, cada uno de los m compradores decide si comprar de la firma I o E.
El modelo predice los siguientes resultados:
- 1.
Equilibrio excluyente. Siempre existirá un equilibrio de Nash en estrategias puras donde I vende a todos los nuevos compradores fijando un precio p1∈0,1 para todo i=1, ...m donde ∑sipi≥cI. Por otra parte, E fija un precio pE∈0,1 tal que pE≤pI para todo i=1, ...m y en todo equilibrio de continuación donde pE≤pI todos los compradores nuevos le compran a I.
- 2.
Equilibrio de entrada. Existe un equilibrio de entrada de estrategia pura para cualquier cE<cI, donde E vende a todos los nuevos compradores y fija un precio pE=pI=cI para todo i. En todo equilibrio de continuación donde pE≤pI todos los compradores le compran a E.
Los resultados expuestos no dependen de si considera o no una demanda simétrica o asimétrica. Por lo tanto, el modelo no explica el efecto de la heterogeneidad en la demanda del consumidor sobre el equilibrio predicho.
El esquema de competencia propuesto por Karlinger y Motta tiene como base teórica un modelo a la Bertrand con productos diferenciados. La implicancia directa es que los bienes de red considerados no son sustitutos perfectos. En el caso de que el producto en cuestión fuese homogéneo, se esperaría equilibrios en estrategias puras típicamente múltiples. Por otra parte, de existir alguna medida de diferenciación en los productos, el equilibrio de Bertrand será típicamente único (Caplin y Nalebuff, 1991, p. 51; Dastidar, 1995, p. 30; Coloma, 2009, p. 52).
2.2Evidencia empíricaAdemás del diseño propuesto en el presente artículo, en la literatura se pueden apreciar varios enfoques similares para encontrar equilibrios excluyentes y equilibrios de entrada, en contextos de competencia monopolística. En el trabajo realizado por Segal y Whinston, al igual que en el de Simpson y Wickelgren, se muestra el potencial de exclusión de contratos exclusivos cuando la empresa I puede discriminar en la oferta realizada a sus compradores, siendo la primera en ofrecer su producto y no permitiendo la renegociación de contratos por parte de sus consumidores. En estos casos, al igual que en el modelo estándar de Bertrand, se obtienen equilibrios múltiples como solución (Segal y Whinston, 2000, pp. 298-299; Simpson y Wickelgren, 2007, pp. 1306).
Por otro lado, un modelo más reciente basado también en el trabajo de Karlinger y Motta es el planteado por Vasconcelos, en el cual se utiliza la misma idea de un bien homogéneo ofrecido por una empresa I y otra E, con la diferencia de que los «nuevos» compradores se dividen en dos segmentos (Vasconcelos, 2015, p. 25). Dichos segmentos están interrelacionados, siendo el consumo del primero dependiente del consumo del segundo. Por esta razón, ambos comprarán el bien a la misma empresa siempre y cuando el precio se mantenga en un rango de aceptación. En ambos segmentos las dos empresas plantean primero su precio y luego los clientes eligen cuál comprar. Otra diferencia importante es que se plantean dos escenarios distintos:
- •
En el primer escenario, la empresa I no posee una base de clientes previos y predomina un equilibrio de entrada.
- •
En el segundo escenario la empresa I sí tiene una base de clientes «antiguos» cuya compra estará garantizada, siendo el equilibrio excluyente el que predomina y ofrece el mayor beneficio social.
En contraste, el mecanismo de exclusión que se estudia en el trabajo de Karlinger y Motta está basado en la discriminación de precios entre los compradores del denominado «segmento competitivo» más que en la discriminación entre los segmentos «competitivo» y «capturado». La intuición es que la firma I puede impedir la entrada de la empresa E si convence a un número suficiente de nuevos compradores a consumir su producto tal que la empresa E no alcance su masa crítica.
La empresa I puede obtener dicho resultado ofreciendo precios por debajo de costo a cierto número de compradores (i.e., m – q¯ + 1). Esta estrategia resultaría rentable para la empresa I solo si esta puede recuperar las pérdidas con los compradores restantes (q¯ – 1), quienes ya no tendrían otra opción más que comprar de la empresa I. Las características propias que muestra este modelo resultan adecuadas para el desarrollo del presente experimento, ya que son una buena aproximación de un mercado con características competitivas de red desarrollado en situaciones realistas (Karlinger y Motta, 2012, p. 76).
Además, Bonne et al. presentan evidencia experimental basada en un modelo de competencia a la Bertrand, cuya arista con lo propuesto por Karlinger y Motta es el esquema de costos unitarios asimétricos y bienes homogéneos pero incompatibles. De la misma manera, siguiendo un esquema de competencia a la Bertrand, Argenton y Müller analizan la colusión en mercados simétricos y asimétricos manteniendo un esquema de costos diferenciados entre firmas (Boone et al., 2012, p. 134; Argenton y Müller, 2012, p. 508).
2.3Diseño experimentalSe utilizó el marco teórico descrito en la sección anterior como base para el diseño de los escenarios a los que los participantes del experimento fueron expuestos. Se construyen dos diferentes escenarios con el fin de contrastar si se observan diferencias sistemáticas en los resultados del ejercicio entre los estudiantes que han sido formados en teoría de juegos y los que no. Además, los resultados teóricos del modelo de Karlinger y Motta (2012) predicen que no se deberían presentar diferencias en los equilibrios observados a partir de la heterogeneidad en la demanda de los consumidores en el juego. El diseño de escenarios considera este aspecto para contrastar dicha aseveración empíricamente. Los escenarios propuestos para esta finalidad fueron: demanda simétrica y demanda asimétrica.
En ambos casos se asume que el número de nuevos consumidores en el mercado es tres m=3, con la diferencia que, en el escenario de demanda simétrica, los tres consumidores demandan la misma cantidad relativa de producto s1=s2=s3=1/3, mientras que en el escenario de demanda asimétrica uno de los consumidores demanda una cantidad relativamente alta del producto s1=s2=k/2, s3=1−k con 1/2<k<2/3. Además, en el escenario simétrico se denomina a los tres consumidores como tipo-bajo (B) y en el escenario asimétrico se denota a los consumidores 1 y 2 como tipo-bajo mientras al consumidor 3 como tipo-alto (A). Estas especificaciones son consistentes con las recomendaciones mencionadas anteriormente, donde se resalta el uso de grupos pequeños para cada repetición, de forma que se incentive el interés de los participantes (Holt, 1999, p. 608).
Asimismo, para ambos escenarios se asume que la masa de consumidores crítica q¯ es tal que son requeridos por lo menos 2 consumidores para una entrada exitosa. De esta manera, en el caso asimétrico, el consumidor tipo A debe ser uno de los dos compradores para que pueda existir entrada. De este modo, si el consumidor de tipo A compra a la firma I, la entrada nunca ocurrirá en el escenario asimétrico. Por ende, el consumidor de tipo A es esencial en el resultado de este escenario.
Por otra parte, para la correcta asignación aleatoria del perfil de jugador, el registro de las decisiones que tomaron los participantes y el cálculo de los resultados se utilizan soportes computacionales de forma que se fortalecen las actividades interactivas del aula. Así, se incorporan procesos establecidos previamente que favorecen la participación de los estudiantes (Villalta et al., 2015, p. 417). Se cuenta con 24 participantes seleccionados de manera aleatoria de una base de 285 estudiantes, quienes se registraron para participar en el evento «Día de Nash» realizado por la Facultad de Ciencias Sociales y Humanísticas de la ESPOL. Los registros para dicho evento tuvieron una duración de cuatro días y estuvieron abiertos para todos los estudiantes de la universidad sin restricción de semestre, edad, carrera, promedio o género. Por ende, existen dos tipos de perfiles de participantes dentro del experimento: los que han estudiado teoría de juegos como parte de su malla curricular y los que aún no lo han hecho. A partir de allí, se busca medir el impacto del conocimiento de este tema sobre la decisión final de sus estrategias.
El rol de los estudiantes en el juego es el de consumidores, teniendo cada juego una duración de 10 rondas y un tiempo predeterminado de respuesta de 15segundos. En cada ronda los participantes juegan ya sea en el escenario simétrico o en el escenario asimétrico, como un jugador de tipoA o un jugador de tipoB. Así mismo, los estudiantes cambian de rol en cada ronda, de modo que se evita que el historial de estrategias seleccionadas influya en su decisión en las rondas subsiguientes, minimizando la posibilidad de que estos pudiesen llegar a optimizar su estrategia de juego. Tal como plantea Shachat y Swarthout, esto tiende a suceder con mayor frecuencia en experimentos que analizan cómo el comportamiento de los individuos se ajusta en la toma de decisiones repetidas (Shachat y Swarthout, 2012, pp. 383-384).
Además, como se puede observar en la tabla 1, se divide a los participantes en 4 grupos. En cada grupo se juegan dos escenarios, considerando que cada uno tiene 3 consumidores que juegan 10 rondas. Se tiene que por cada escenario participan 3 consumidores, es decir, existen 3 elecciones de compra individuales por escenario. Esto resulta en un total de 120 elecciones de compra por escenario. A su vez, al final de cada ronda se determina la entrada/no entrada de la empresa E por cada escenario, totalizando 40 de estas instancias en cada uno. Esto resulta en un total de 80 observaciones para la entrada/no entrada de la empresa E en el experimento.
Finalmente, Holt realiza una minuciosa descripción de cómo experimentos en el área de microeconomía, teoría de juegos y economía experimental pueden ser dirigidos por estudiantes que muestren un buen desempeño y cursen los últimos años de estudios de pregrado de la carrera del área correspondiente, ya que se encuentran en la capacidad de comprender el experimento en su totalidad (Holt, 1999, p. 608). Por esta razón el diseño experimental propuesto fue dirigido por un grupo de tres estudiantes de cuarto año en coordinación con un profesor de la carrera de Economía, de forma que esta combinación de enseñar y aprender pueda tener resultados relevantes en términos del interés y aprendizaje del estudiante.
2.4Valores de demanda y ofertaEs importante destacar que las proporciones y cantidades seleccionadas para los parámetros experimentales fueron escogidas así para respetar la estructura del modelo descrito en la sección anterior. En cada ronda los participantes obtienen su valoración personal del bien (disposición de pago). Este valor cambia por ronda y es completamente aleatorio dentro de un intervalo 10,100. Los pagos son determinados por la diferencia entre su valoración personal y el precio ofertado, siempre y cuando hayan decidido comprarle a la firma que alcanzó el tamaño crítico al final de la ronda. En caso contrario, el pago recibido es cero.
Los precios son fijados de manera exógena por medio de un algoritmo de simulación en computadora ejecutado previamente. Estos se determinan por la relación de equilibrio entre el precio y el costo marginal. En cada ronda, el costo marginal de la firma I es aleatorio en el intervalo [5,10] y ampliado por la valoración personal, mientras que el costo marginal de la firma entrante es aleatorio obtenido dentro de un intervalo 0,cI.
2.5Descripción del juegoComo ya se mencionó, en cada una de las 10 rondas se juega con dos grupos de tres personas asignadas aleatoriamente en dos escenarios, uno simétrico y otro asimétrico. Al inicio de cada ronda se presenta a todos los jugadores un conjunto de instrucciones estandarizadas (anexo 1) de forma que se sigue la sugerencia propuesta por Holt que permitirá la réplica científica del experimento (Holt, 1999, pp. 606-607). Además, a cada jugador se le proporciona la siguiente información:
- •
Tipo de jugador. Si el participante representa a un consumidor tipo A o tipo B.
- •
Valor personal. Representa el valor monetario que cada consumidor da al bien ficticio, el cual es el mismo para los otros dos participantes de la ronda.
- •
Demanda individual. Número de bienes demandados en cada ronda.
- •
Precio establecido. Valor al que ofrece el producto la empresa I.
- •
Precio entrante. Valor al que ofrece el producto la empresa E.
Una vez observado el precio que ofrecen las empresas, debe decidir entre comprar el producto ficticio ofrecido por la empresa I u optar por la empresa E. Después de que todos los consumidores hayan tomado una decisión se procede a indicar si efectivamente la empresa E logró ingresar al mercado.
3Resultados3.1Recolección de datosEl juego se realizó en un aula de clases adecuada de forma que permitiera controlar el experimento acorde a los parámetros mencionados en el diseño experimental y evitar interacciones de forma que se pudiese contaminar los resultados. Previo al inicio del juego se realizó una encuesta a cada participante, en la que se recogen distintas covariantes idiosincráticas de cada uno de los involucrados en el ejercicio. Asimismo, se considera que el uso de pequeños incentivos durante el juego puede ser de utilidad, debido a que se reduce el ruido en las decisiones y aumenta el interés de los estudiantes (Holt, 1999, p. 606). Por esta razón se entregó un premio no pecuniario al ganador de cada juego. Posteriormente los participantes fueron divididos en 4 grupos distintos y se explicaron los diferentes aspectos que estos debían considerar para tomar una decisión, entre los cuales se planteaba: escenario, precios ofrecidos por las empresas, demanda y valor personal.
Entre las covariantes idiosincráticas consideradas se encuentra que del total de los jugadores el 62% fueron mujeres, la mayor parte de los participantes cursan su segundo año de estudio, cuentan con una edad promedio de 20 años y un promedio académico general de 7,93 sobre 10 con una desviación estándar de 0,5 puntos en esta escala. De la misma forma, el 21% de los participantes informaron tener conocimientos previos sobre teoría de juegos.
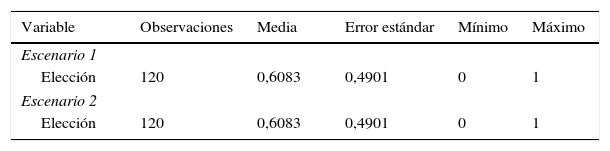
La tabla 2 muestra un resumen de los resultados de la elección de los consumidores que arrojó el experimento:
La variable denominada «Elección» es una variable binaria que toma el valor de 1 si escoge la empresa E y 0 caso contrario. Se observa que la proporción de veces que es escogida la empresa E es mayor al 50% en ambos escenarios.
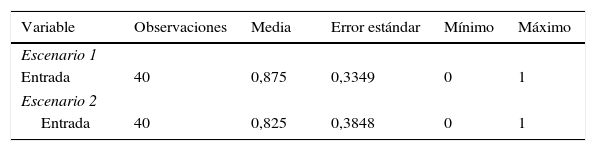
La tabla 3 muestra la variable «Entrada», la cual mide el ingreso exitoso de la empresa E. Es decir, esta indica cuándo alcanzó la masa crítica del mercado, tomando el valor de 1 cuando E logra la entrada al mercado y 0 caso contrario. De esta forma, su media representa la proporción de veces que E alcanza la masa crítica. Se puede observar que se logró la entrada de la empresa E en más del 80% de las veces independientemente del escenario, por lo que el equilibrio observado más frecuente es el equilibrio de entrada motivado en la sección 2.1. Naturalmente, para poder responder las preguntas de fondo según el efecto del escenario respecto al equilibrio de entrada, se elabora un modelo de regresión que será expuesto en la siguiente subsección.
3.2Modelo econométricoEn primer lugar se busca analizar el efecto que los parámetros del diseño experimental tienen sobre la decisión individual de compra. Para esto se toma en cuenta que es necesario controlar por los covariantes idiosincráticas de los jugadores que afectan la decisión, más allá del efecto que pudiesen mostrar los parámetros experimentales. Entre estos se consideró relevante si el estudiante había tomado un curso previo de teoría de juegos o no, ya que esto puede predisponer el comportamiento estratégico por parte del jugador. Como mencionan Arroyo et al., si se define el conocer acerca de teoría de juegos como una ventaja por encima de alguien que no, es necesario evaluar la importancia de la ventaja al hacer comparaciones entre ellos (Arroyo et al., 2015, p. 7). Otra característica idiosincrática de los jugadores considerada en el experimento fue el género, ya que estudios anteriores han demostrado que existen diferencias en las decisiones entre hombres y mujeres en contextos competitivos (Croson y Gneezy, 2009, p. 464).
Al tratarse de un juego repetido en donde se busca contrastar equilibrios de continuación empíricamente, las decisiones individuales de compra se modelan a través de un panel que considera la elección de los 24 participantes a través de las 10 rondas que estos juegan. La estimación del efecto marginal de las variables mencionadas se realiza por medio de un modelo de probabilidad lineal (MPL) utilizando mínimos cuadrados ordinarios agregados (MCOA). Si bien las limitaciones de este procedimiento son ampliamente discutidas en la literatura, el interés del presente estudio radica en estimar los efectos marginales de las covariantes exploradas sobre la decisión de compra individual. Wooldridge y Angrist y Pischke mencionan que las aproximaciones producidas por el MPL para los efectos marginales son comparables a otros tipos de modelos de decisión no-lineales para valores que se encuentran cercanos a los promedios de la muestra utilizada (Wooldridge, 2012, p. 251; Angrist y Pischke, 2008, p. 80). Por esta razón, se utilizará este procedimiento adoptando las correcciones sugeridas en la literatura de forma que se puedan mejorar las propiedades muestrales de los estimadores obtenidos para los efectos marginales en cuestión. El procedimiento se resume a continuación:
- 1.
Estimar el MPL corrigiendo la varianza por medio de la estimación robusta por conglomerados definidos para cada participante a fin de lidiar con la heterocedasticidad implícita en los términos de error de un MPL (Angrist y Pischke, 2008).
- 2.
Para mejorar las propiedades muestrales de la estimación por MPL se sigue el procedimiento sugerido por Horrace y Oaxaca (2006, pp. 322-326). Para ello, se estima el modelo acorde con lo establecido en el paso anterior y se obtienen las predicciones para cada observación, yˆt=Xiβˆ. Luego se trunca la muestra a partir de la regla yˆt∉0,1 y se re-estima el modelo MPL a partir de la submuestra resultante siguiendo lo establecido en el paso anterior.
Una vez descrito el procedimiento de estimación utilizado, es necesario apuntar que la especificación del modelo considera el impacto de cursar teoría de juegos sobre los efectos marginales de los parámetros de diseño del experimento por medio de interacciones. También se controló por los grupos especificados en el diseño del experimento con el fin de probar la fidelidad del mismo, ya que estos no deben afectar la decisión de compra bajo muestreo aleatorio simple. De igual forma se controló por cada ronda del juego para contrastar que no se produzcan efectos de aprendizaje (lo cual se buscó controlar por diseño mediante la aleatorización del escenario que le tocó a cada jugador en las distintas rondas).
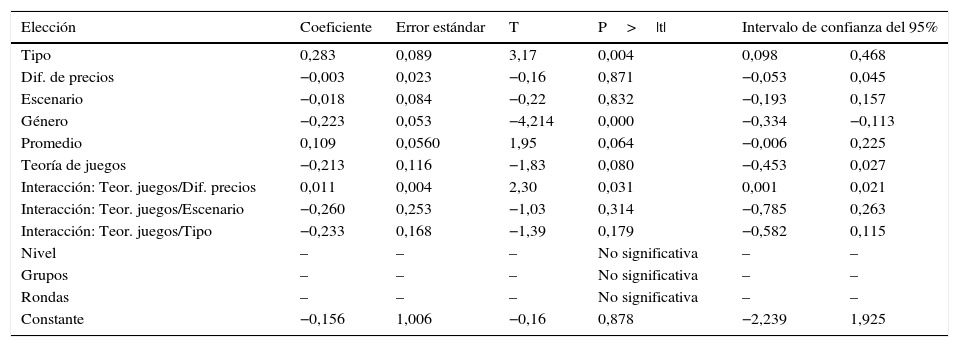
La tabla 4 resume el resultado de la estimación de MPL por el procedimiento descrito. Se puede observar que las variables tipo de consumidor, género y la interacción entre la diferencia de precios y la variable teoría de juegos son significativas. Por otro lado, se destaca que el promedio general del estudiante y el nivel académico que cursa no resultaron ser variables estadísticamente significativas.
Regresión MPL de la elección de la empresa entrante sobre variables de control y propias de cada individuo
| Elección | Coeficiente | Error estándar | T | P>|t| | Intervalo de confianza del 95% | |
|---|---|---|---|---|---|---|
| Tipo | 0,283 | 0,089 | 3,17 | 0,004 | 0,098 | 0,468 |
| Dif. de precios | −0,003 | 0,023 | −0,16 | 0,871 | −0,053 | 0,045 |
| Escenario | −0,018 | 0,084 | −0,22 | 0,832 | −0,193 | 0,157 |
| Género | −0,223 | 0,053 | −4,214 | 0,000 | −0,334 | −0,113 |
| Promedio | 0,109 | 0,0560 | 1,95 | 0,064 | −0,006 | 0,225 |
| Teoría de juegos | −0,213 | 0,116 | −1,83 | 0,080 | −0,453 | 0,027 |
| Interacción: Teor. juegos/Dif. precios | 0,011 | 0,004 | 2,30 | 0,031 | 0,001 | 0,021 |
| Interacción: Teor. juegos/Escenario | −0,260 | 0,253 | −1,03 | 0,314 | −0,785 | 0,263 |
| Interacción: Teor. juegos/Tipo | −0,233 | 0,168 | −1,39 | 0,179 | −0,582 | 0,115 |
| Nivel | – | – | – | No significativa | – | – |
| Grupos | – | – | – | No significativa | – | – |
| Rondas | – | – | – | No significativa | – | – |
| Constante | −0,156 | 1,006 | −0,16 | 0,878 | −2,239 | 1,925 |
Fuente: elaboración propia.
Así, los principales resultados que se pueden recoger de la tabla 4 se resumen a continuación:
- •
No existe un efecto significativo del escenario, a nivel individual, sobre la probabilidad de que los jugadores elijan el producto de la empresa E o el de la empresa I.
- •
En promedio, la probabilidad de elegir la empresa E sobre la I de un consumidor tipo A es un 28,37% mayor que la de un consumidor tipo B.
- •
En promedio, la probabilidad de elegir la empresa E sobre la I de un hombre es alrededor del 22% menor que la de una mujer.
- •
El efecto estimado para la diferencia de precios se dividirá en dos subgrupos. Para los estudiantes que conocen la teoría de juegos, un incremento de $1 en la diferencia de precios ofrecidos tendrá un efecto promedio de alrededor del 1,13% de aumento en la probabilidad de elegir a la empresa E sobre la I. Para los jugadores que no han estudiado teoría de juegos, la misma diferencia en los precios ofrecidos no produce un efecto significativo en la probabilidad de elegir la empresa E sobre la I.
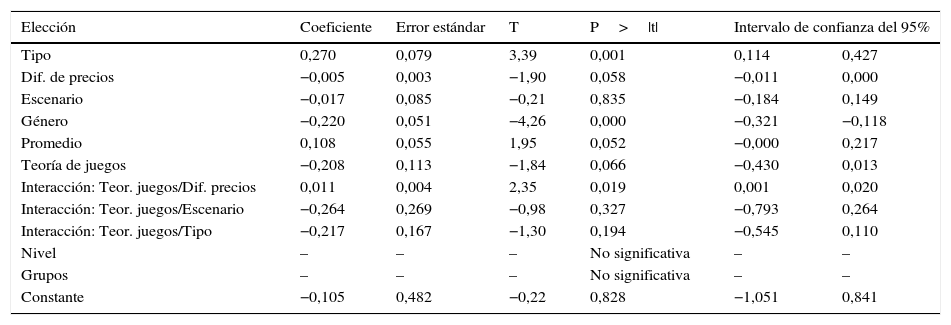
Por otra parte, dado que el modelo MPL se estima mediante MCOA, se proporciona también la estimación de mínimos cuadrados generalizados factibles (MCGF) para el modelo considerando efectos aleatorios1. La tabla 5 muestra los resultados de este ejercicio, el cual se realiza con la finalidad de validar las conclusiones a las que se llega en base a la especificación anterior. A partir de esto, se puede observar que no existe diferencia respecto a lo encontrado con el modelo estimado por MCOA, lo cual verifica la validez de las conclusiones.
Regresión de MCGF de la elección con efectos aleatorios
| Elección | Coeficiente | Error estándar | T | P>|t| | Intervalo de confianza del 95% | |
|---|---|---|---|---|---|---|
| Tipo | 0,270 | 0,079 | 3,39 | 0,001 | 0,114 | 0,427 |
| Dif. de precios | −0,005 | 0,003 | −1,90 | 0,058 | −0,011 | 0,000 |
| Escenario | −0,017 | 0,085 | −0,21 | 0,835 | −0,184 | 0,149 |
| Género | −0,220 | 0,051 | −4,26 | 0,000 | −0,321 | −0,118 |
| Promedio | 0,108 | 0,055 | 1,95 | 0,052 | −0,000 | 0,217 |
| Teoría de juegos | −0,208 | 0,113 | −1,84 | 0,066 | −0,430 | 0,013 |
| Interacción: Teor. juegos/Dif. precios | 0,011 | 0,004 | 2,35 | 0,019 | 0,001 | 0,020 |
| Interacción: Teor. juegos/Escenario | −0,264 | 0,269 | −0,98 | 0,327 | −0,793 | 0,264 |
| Interacción: Teor. juegos/Tipo | −0,217 | 0,167 | −1,30 | 0,194 | −0,545 | 0,110 |
| Nivel | – | – | – | No significativa | – | – |
| Grupos | – | – | – | No significativa | – | – |
| Constante | −0,105 | 0,482 | −0,22 | 0,828 | −1,051 | 0,841 |
Fuente: elaboración propia.
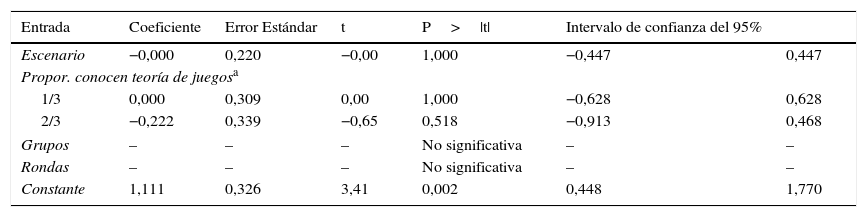
Por otra parte, la tabla 6 presenta la estimación de un segundo modelo, el cual muestra el efecto estadístico del escenario sobre la entrada de la empresa E. Para ello, se sigue la misma estrategia delineada anteriormente con el fin de producir estimaciones del MPL con propiedades muestrales deseables. Sin embargo, se modifica el paso1, ya que no se puede ajustar la varianza de la misma forma debido a que la entrada de la empresa E se produce a partir de la agregación de las decisiones de los jugadores en cada ronda. En su lugar, se corrige la varianza por el método de White para lograr el mismo efecto (Wooldridge, 2012, p. 279).
Regresión MPL de la entrada con respecto al escenario
| Entrada | Coeficiente | Error Estándar | t | P>|t| | Intervalo de confianza del 95% | |
|---|---|---|---|---|---|---|
| Escenario | −0,000 | 0,220 | −0,00 | 1,000 | −0,447 | 0,447 |
| Propor. conocen teoría de juegosa | ||||||
| 1/3 | 0,000 | 0,309 | 0,00 | 1,000 | −0,628 | 0,628 |
| 2/3 | −0,222 | 0,339 | −0,65 | 0,518 | −0,913 | 0,468 |
| Grupos | – | – | – | No significativa | – | – |
| Rondas | – | – | – | No significativa | – | – |
| Constante | 1,111 | 0,326 | 3,41 | 0,002 | 0,448 | 1,770 |
Se puede observar que, con un 95% de confianza, no se rechaza la H0, que plantea que la probabilidad de entrada de la empresa E es la misma en ambos escenarios. También se muestra una variable categórica que representa cuántas de las personas en cada grupo conocen sobre teoría de juegos; sin embargo, no resulta significativa en ninguna de sus categorías. Así mismo, el hecho de que la constante resulta significativa muestra que la probabilidad de entrada de la empresa E es distinta de 0 y que no hay diferencia en los parámetros de control de experimento para esta medida. Finalmente, es importante notar que en esta regresión también se controla por rondas y grupos especificados en el diseño del experimento, debido a las mismas razones expresadas anteriormente.
4Conclusiones y recomendacionesMediante el presente ejercicio académico se logró recoger varios resultados interesantes, entre los cuales destaca el hecho de que no se observó un efecto estadísticamente significativo del escenario experimental respecto de la decisión de la entrada de la nueva empresa en el mercado. En el caso de la compra individual, la variable escenario tampoco resulta estadísticamente significativa; sin embargo, la variable tipo de jugador afecta directamente a la decisión de compra; es decir, la asimetría entre consumidores es relevante al momento de tomar decisiones individuales. Dicho resultado difiere de lo demostrado teóricamente en el modelo original de Karlinger y Motta, e indica que las estrategias de los estudiantes inmersos en el experimento muestran alteración respecto al tipo de jugadores que intervienen en la decisión de compra pero no en el resultado agregado. Es posible que el efecto de la variable escenario sea capturado por la variable tipo, en cuyo caso podría existir correlación entre la variable escenario y la presencia del consumidor de tipoA. De acuerdo al modelo propuesto, esto tiene un efecto significativo sobre la decisión de compra, así como la entrada de la empresa E, lo que significa que la asimetría entre consumidores sí importa.
No obstante, se recoge que la tendencia observada para la decisión individual de compra de los jugadores que representaban consumidores tipoA es un 27% más probable a inclinarse hacia la compra del bien ofrecido por la empresa E. Así mismo, se encontró que el género y el hecho de tener conocimientos acerca de teoría de juegos, considerándola como una ventaja, son covariantes idiosincráticas que afectan la decisión de compra de los estudiantes, apoyando las hipótesis planteadas anteriormente (Croson y Gneezy, 2009, p. 464; Arroyo et al., 2015, p. 7). En particular, el último de estos afecta el modo en que el precio ofertado a los jugadores determina las estrategias de compra individual de los mismos, encontrándose que los estudiantes que fueron expuestos a esta formación tienen tendencia a escoger la empresa entrante cuando la diferencia de los precios ofertados aumenta, mientras que los jugadores no expuestos previamente a teoría de juegos no muestran una reacción significativa con respecto a los precios ofertados por ambas empresas.
A partir de esto se hace énfasis en que uno de los hallazgos más importantes del presente artículo es la relevancia de conocimientos previos acerca de teoría de juegos para la toma de decisiones de los estudiantes en un ambiente competitivo, independientemente del desempeño académico de cada uno medido a través del promedio general. De igual manera, la aplicación de teoría de juegos en diversos campos contribuye al desarrollo de técnicas durante el proceso enseñanza-aprendizaje (Burguillo, 2010, p. 567), y también permite que el conocimiento teórico sea más accesible (Ebner y Holzinger, 2007, pp. 874-875), aumentando la motivación intrínseca de los estudiantes y, como consecuencia, un mejor desempeño académico.
Finalmente, el diseño experimental propuesto para el modelo teórico de Karlinger y Motta (2012) podría explorarse más a fondo, replicando dicho experimento con representantes de empresas reales. De confirmarse lo encontrado en el presente trabajo para ese perfil de usuarios, se podría intuir que una empresa que desee entrar en un mercado con las características descritas tendrá mayores probabilidades de éxito si enfoca sus políticas de precio a compradores grandes. Bajo este mismo argumento, la empresa establecida I podría inclusive impedir la entrada de nuevas empresas al mercado, enfocando sus esfuerzos comerciales a este tipo de consumidores. De hecho, el experimento sugiere que el escenario excluyente es poco frecuente, debido básicamente a que la empresa E tiene costos más bajos; si dichos costos fueran similares a la empresa I, los resultados podrían variar. Otro aspecto importante a explorar sería el efecto del conocimiento estratégico revelado por dichos jugadores, similar a lo recogido en el presente ejercicio a través de la exposición a la educación en teoría de juegos.
- •
Por favor, lea las instrucciones cuidadosamente.
- •
Por favor, no hable con sus vecinos y manténgase en silencio durante todo el experimento.
- •
Si tiene una pregunta, levante la mano. Iremos hasta su puesto a responderla.
- •
Usted participará en un experimento como un consumidor ficticio de un producto que se le ofrece por medio de dos firmas: una que ya está establecida en el mercado (I) y otra es una entrante potencial a dicho mercado (E).
- •
Para obtener valor por consumir el producto, debe comprarlo de una firma que ha alcanzado un tamaño crítico en el mercado. Esto es, tiene que comprar el producto de una firma que haya obtenido un mínimo número de consumidores.
- •
Antes de jugar, se sabe que la firma I ya tiene el tamaño crítico, pero la firma E está planificando entrar al mercado y no tiene consumidores.
- •
Cada uno de ustedes juega con otros 2 participantes durante 10 rondas, y en cada una será aleatoriamente asignado a jugar con otros 2 participantes.
- •
En cada ronda tendrá que escoger si decide comprar el producto de la firma I o el de la firma E.
- •
Al empezar cada ronda se publican los precios de ambas firmas, después de lo cual usted toma su decisión.
- •
Al terminar cada ronda, se le informará si usted fue exitoso o no.
- •
En cada ronda usted puede ser un consumidor de tipo A o B. Esto será determinado de manera aleatoria en cada ronda.
- •
Su tipo determina el total de unidades de producto que desea comprar. Los tipos A siempre querrán comprar más unidades que los consumidores de tipo B. Más aún, consumidores distintos del tipo B siempre consumirán el mismo número de unidades.
- •
Si en una ronda se juega como un consumidor tipo B, se puede enfrentar a 2 posibles escenarios:
- 1.
Uno de los otros jugadores es consumidor tipo A y el otro es tipo B.
- 2.
Los otros dos jugadores son consumidores tipo B.
- 1.
- •
Si en una ronda se juega como un consumidor tipo A se sabe con seguridad que los otros 2 son de tipo B, y además se encuentra necesariamente en el escenario 1.
- •
En cada ronda se le informará en qué escenario se está jugando (1 o 2).
- •
En ambos escenarios, los consumidores tipo B tendrán la misma demanda, esto es, demandarán las mismas unidades de producto en cualquier ronda. Note que el «valor privado» y la cantidad demanda pueden cambiar entre ronda, pero siempre todos los consumidores tipo B demandarán lo mismo.
- •
En cada ronda se le dará un valor monetario que representa el beneficio por consumir el producto demandado en caso de ser exitoso.
- •
Este valor será el mismo para los otros 2 consumidores con los que está jugando.
- •
Si se escoge comprar de la firma I, su pago estará dado por su valor privado menos el precio al que I ofrece el producto, multiplicado por su cantidad demandada.
- •
Si escoge comprar de la firma E, su pago será dado por:
- ∘
Su valor privado menos el precio ofertado por E multiplicado por la cantidad demandada si la entrada de la firma E fue exitosa (revise la última sección).
- ∘
Cero si la entrada no fue exitosa.
- ∘
Note que si escoge comprarle a la firma I siempre va a obtener un pago mayor a cero siempre que su valor privado sea mayor al precio ofertado.
- ∘
- •
Escenario 1. La entrada es exitosa si al menos un consumidor tipo A y un tipo B escogen la firma E.
Ejemplo:
- ∘
Si usted es un consumidor tipo B, la entrada de la firma E será exitosa si usted y un consumidor tipo A consumen de E. Esto implica que si el consumidor tipo A escoge la firma I, la entrada no será exitosa.
Combinaciones posibles de entrada exitosa:
- •
A y B1 compran de E, mientras B2 compra de I.
- •
A y B2 compran de E, mientras B1 compra de I.
- •
A, B1 y B2 compran de E.
- •
- ∘
- •
Escenario 2. La entrada de la firma E será exitosa si al menos 2 consumidores tipo B escogen comprar de la firma E.
Ejemplo:
- ∘
La entrada será exitosa si usted y al menos otro consumidor más escogen comprar el producto a la firma E.
Combinaciones posibles de entrada exitosa:
- •
B1 y B2 compran de E y B3 compra de I.
- •
B1 y B3 compran de E y B2 compra de I.
- •
B2 y B3 compran de E y B1 compra de I.
- •
B1, B2 y B3 compran de E.
Como se puede constatar en Cameron y Trivedi (2005), si bien el estimador MCOA es consistente bajo exogeneidad estricta, el estimador MCGF para el modelo de efectos aleatorios es más eficiente.