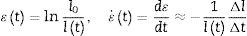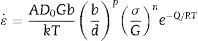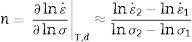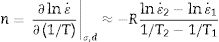The high temperature mechanical properties of polycrystalline Y2SiO5 were studied in compression at temperatures in the range of 1200–1400°C, both in constant strain rate and constant stress experiments. To examine the effect of grain size on the plastic deformation, two routes were used for the synthesis and sintering of Y2SiO5: one of solid state reaction followed by conventional sintering in air, and one of sol–gel synthesis followed by spark-plasma sintering, resulting in starting grain sizes of 2.2 and 0.9μm, respectively. Ceramics obtained by these routes exhibited different high-temperature compression behavior: while the conventionally processed ceramic exhibited grain growth during mechanical testing and a stress exponent close to one, compatible with diffusional creep, the spark-plasma sintered ceramic showed no grain growth but significant cavitation, a stress exponent close to two and partially superplastic behavior. These results have implications for the design and lifetime assessment of rare earth silicate-based environmental barrier coatings.
Este trabajo aborda el comportamiento mecánico a compresión del Y2SiO5 policristalino a temperaturas entre 1200°C y 1400°C, tanto en experimentos de tensión constante como de velocidad de deformación constante. Para estudiar el efecto del tamaño de grano en la deformación plástica, se utilizaron dos rutas para la síntesis y sinterización de Y2SiO5: una de reacción en estado sólido seguida de sinterización convencional en aire, y una de síntesis sol-gel seguida de Spark-Plasma Sintering, obteniéndose tamaños de grano iniciales de 2,2 y 0,9μm, respectivamente. Los policristales obtenidos por estas rutas mostraron distinto comportamiento en compresión a alta temperatura: mientras que el cerámico convencionalmente exhibió crecimiento de grano y un exponente de tensión cercano a uno, compatible con un mecanismo de fluencia por difusión, el cerámico procesado por Spark-Plasma Sintering no mostró crecimiento de grano pero sí cavitación, un exponente de tensión cercano a 2 y un comportamiento parcialmente superplástico. Estos resultados tienen implicaciones para el diseño y la evaluación de la vida útil de recubrimientos de barrera ambiental a base de silicatos de tierras raras.
Ceramic matrix composites (CMCs) and silicon-based ceramics (such as Si3N4, SiC) are promising candidates for high temperature structural applications such as next generation gas turbine engines since they exhibit low density, excellent high-temperature mechanical properties, and good thermo-mechanical stability [1,2]. In presence of oxygen from dry air environments, silicon-based ceramics form a protective silica scale, responsible for their excellent high temperature oxidation resistance at these conditions [3]. However, this SiO2 layer is susceptible of attack by impurities such as alkali salts and is unstable in the presence of water vapor, resulting in rapid ceramic recession. Thus, Si-based ceramics present a lack of environmental durability [4–6].
Currently, environmental barrier coatings (EBCs) are being used to limit the volatilization and recession of the passivating oxide layer, extending the operating conditions of SiC based ceramics in combustion environments [7]. Rare earth silicates (such as yttrium silicates) are being explored as topcoats in third-generation EBCs [8–11] due to their low thermal expansion coefficient, thermochemical stability and higher temperature capability than current generation EBCs formed of mullite and barium-strontium aluminosilicates (BSAS) [12–14]. Yttrium silicates (e.g., yttrium orthosilicate, Y2SiO5) are promising materials for improving oxidation and erosion protection since they exhibit a high melting point, low volatilization rate, low thermal expansion coefficient, and low oxygen permeation constant [15,16]. There are several synthesis methods to obtain Y2SiO5 powders such as solid-state reaction, sol-gel, and hydrothermal methods [17–19]. Nevertheless, the preparation of single-phase fully dense Y2SiO5 bulk material by these methods presents several problems [20–22] such as presence of secondary undesired phases, significant porosity in bulk samples, etc.
Despite the interest in rare earth silicates as topcoats for EBCs, and while room temperature mechanical properties and thermal properties of Y2SiO5 polycrystalline materials have been studied in detail [22–24], little is known regarding their high-temperature mechanical properties and, to the authors’ knowledge, no data on the creep behavior of these materials has been published. In EBC multilayers, the topcoat is subjected to stresses that arise from the thermal expansion mismatch between the different layers that form the coating, which can vary from tensile to compressive as the EBC is thermally cycled during operation [25] and can be affected by reaction with molten glass deposit within engines [26]. Thus, it is necessary to understand Y2SiO5 behavior at high temperatures to evaluate its performance and lifetime for structural components and coatings for high temperature applications.
The aim of this work is then to study the mechanical properties of Y2SiO5 at temperatures that are relevant for their actual applications as elements of EBCs. To this end, we prepared Y2SiO5 ceramics via two different routes with the goal of obtaining ceramics with different microstructures. Then, the obtained ceramics were tested at temperatures in the range 1200–1350°C in compression to determine their high-temperature plasticity and creep behavior. The change of creep behavior is discussed as a function of preparation route and grain size.
Experimental methodsSynthesis and sintering of Y2SiO5 ceramicsTwo processing routes for Y2SiO5 were used in this work with the aim of obtaining ceramics with different grain sizes: solid state reaction followed by conventional sintering and sol–gel synthesis followed by spark-plasma sintering (SPS). The former process is expected to result in polycrystals with a larger grain size compared to the later one.
For conventional sintering, Precursor powders of Y2O3 (Sigma–Aldrich, 99.99%) and amorphous SiO2 (Sigma–Aldrich, 99.95%) were mixed in stoichiometric ratios (1:1 molar) in isopropyl alcohol. To this mixture 3% mol. LiYO2 was added as a sintering additive [20,27] and the resulting powder was milled in a planetary mill for 10h and then calcined at 1500°C for 2h in air. The resulting powders were ball-milled again for 10h to break all agglomerates and to achieve a homogeneous particle size. These powders were uniaxially pressed in a 13mm diameter steel die at 100MPa and then isostatically cold pressed at 200MPa to form a green-body compact (density ∼65–70%) that was subsequently sintered in a furnace at 1500°C in air for 6h.
For the second processing route, methods were adapted from a previous publication on La9.33Si6O26[28]. For the synthesis, commercially available reagents yttrium acetate Y(CH3COO)3·H2O (Alfa Aesar, 99,9%) and tetraethoxysilane Si(OC2H5)4 (TEOS, Alfa Aesar 99,9%) were used as precursors of Y3+ and Si4+ cations. Firstly, two solutions were prepared: one with ∼16–17g of yttrium acetate completely dissolved into ultra-pure water, and another containing ∼6.7mL silicon alkoxide, ∼27mL acetic acid and a small quantity of ultra-pure water. Acetic acid was used as double agent since it catalyzes and controls the hydrolysis reaction of TEOS. Then, the second solution was poured into the first one and mixed thoroughly. The total volume of the solution obtained was 600mL, with a pH value close to 3.8. After that, strong stirring was carried out for 2h to obtain a clear transparent solution. This solution was sprayed into a liquid nitrogen bath to form frozen droplets that were transferred to a freeze-dryer in as short a time as possible to avoid melting. Freeze-drying was carried out in a Christ Alpha 2–4 LSC apparatus for 72h under vacuum (1Pa), with the condenser temperature fixed at −80°C. Once this process was completed, the resulting white porous powder was calcined in air at 1400°C for 4h.
These powders were sintered using SPS to achieve fully dense materials using a graphite die 20mm in diameter in a Dr. Sinter 2080 SPS furnace (Plateforme Fritage Flash, Thiais, France). The applied pressure was 100MPa and the temperature was increased to 600°C at a rate of 200°Cmin−1 and then to 1200°C at a rate of 50°Cmin−1. This temperature was held for 3min before releasing the applied pressure and heating power. Natural cooling took around 10min; thus, the entire process was undergone in less than one hour. Finally, the sintered ceramics were heated at 800°C for 24h in air to remove residual carbon coming from the graphite die.
CharacterizationDensity of the sintered ceramics was determined using a He-Pycnometer (Quantachrome Ultrapyc 1200e). Relative density was calculated from the theoretical density of Y2SiO5 (4.44gcm−3) and under the hypothesis that the synthesis reaction was complete and thus the whole sintered pellet contains only Y2SiO5.
Samples both as-fabricated and after mechanical testing were observed using a scanning electron microscope (SEM, FEI Teneo) and a transmission electron microscope (TEM, FEI Talos). For SEM observations samples were cut using a diamond coated wafering blade and polished by conventional metallographic methods using diamond abrasives down to 1μm. To enhance the grain boundary contrast and facilitate the determination of grain size, samples were further thermally etched in air at 1300°C for one hour. Grain size was determined using the linear intercept method. For TEM observation samples were cut into 3mm disks and thinned abrasively down to 100μm before dimpling and ion polishing.
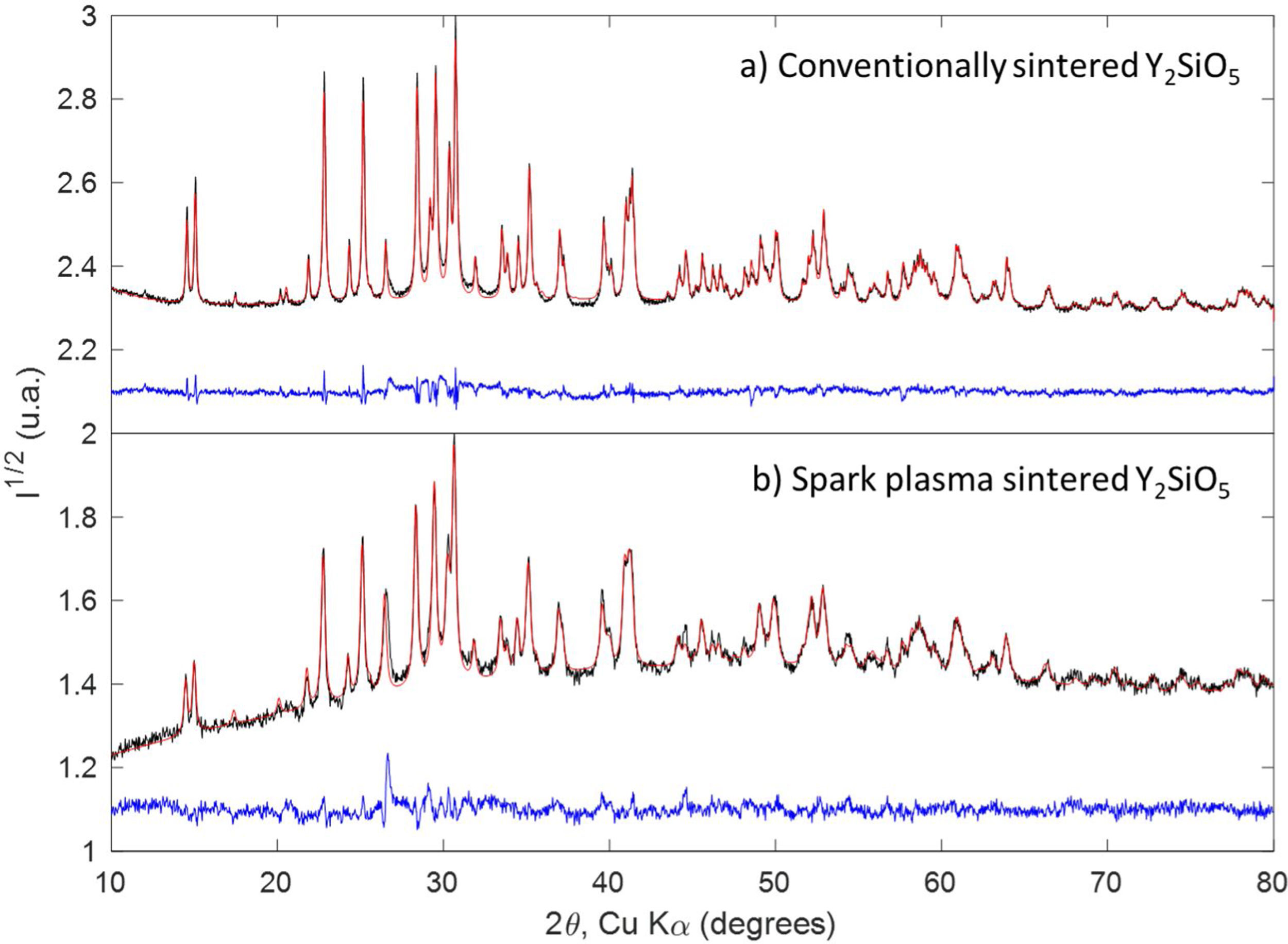
The identification of crystalline phases in the sintered Y2SiO5 ceramics was performed using X-ray diffraction (XRD, D8 Advance 24, Bruker). Each pattern was measured at following conditions: Bragg-Brentano configuration θ–2θ using Cukα wavelength (λ=1.5418Å) filtered with a nickel foil in a XRD tube at voltage 40kV and current intensity of 30mA. Data acquisition was by means of continuous angular scanning in the 2θ region between 10° and 90° with a 0.03° step in 2θ. The resulting diffractograms were analyzed by the Rietveld method. Starting crystal structures were obtained from the PDF-4+2019 crystallographic database (International Centre for Diffraction data) for Y2SiO5 (PDF 00-036-1476) and Y2O3 (PDF 00-041-1105). The Fundamental Parameters approach was used to model instrumental peak broadening and the following parameters were refined: lattice parameters, sample displacement, Lorentzian broadening due to crystallite size, a 5-order Chebyshev polynomial to describe the background and a global scaling constant.
Mechanical testingSamples were cut into parallelepipeds (3mm×3mm×5mm) for mechanical testing and the load was applied in compression along the longest direction in all cases. Each sample's faces were ground plane-parallel using a diamond grinding wheel. Two types of experiments were performed: constant strain rate and constant stress.
Constant strain rate experiments were performed in an electromechanical Universal Testing Machine (Microtest EM1/50/FR) with an attached furnace. Load was applied using two 25.4mm diameter alumina rods. Starting strain rate was in all cases 3.2×10−6s−1 (the lowest attainable rate in our system) and the load was monitored using either a 1kN or 5kN rated load cell, depending on the temperature and load range. The tested temperatures were in the range of 1200–1350°C. Samples were subjected to a small contact load that was maintained during heating at 10°C/min until the final temperature, which was held for 1h before the start of each test to allow for thermal stabilization of the system.
Constant stress (creep) experiments were carried out using a dead-weight machine (Microtest M/SCM-2-FP) in which the load is applied using a lever connected to the upper loading rod, while the lower rod is displaced to ensure constant stress. Sample contraction during the experiments was monitored using a linear variable displacement transducer outside the hot zone of the furnace, attached to the machine's frame. Strain and strain rates were determined from the instantaneous length l(t) of the sample using:
Applied stresses were in the range of 20–60MPa and temperatures were in the range 1300–1400°C. As in the case of constant strain-rate experiments, samples were subjected to a small contact load that was maintained during heating, which was carried out at 10°C/min until the final temperature. A soaking time of 1h was allowed before the start of each.
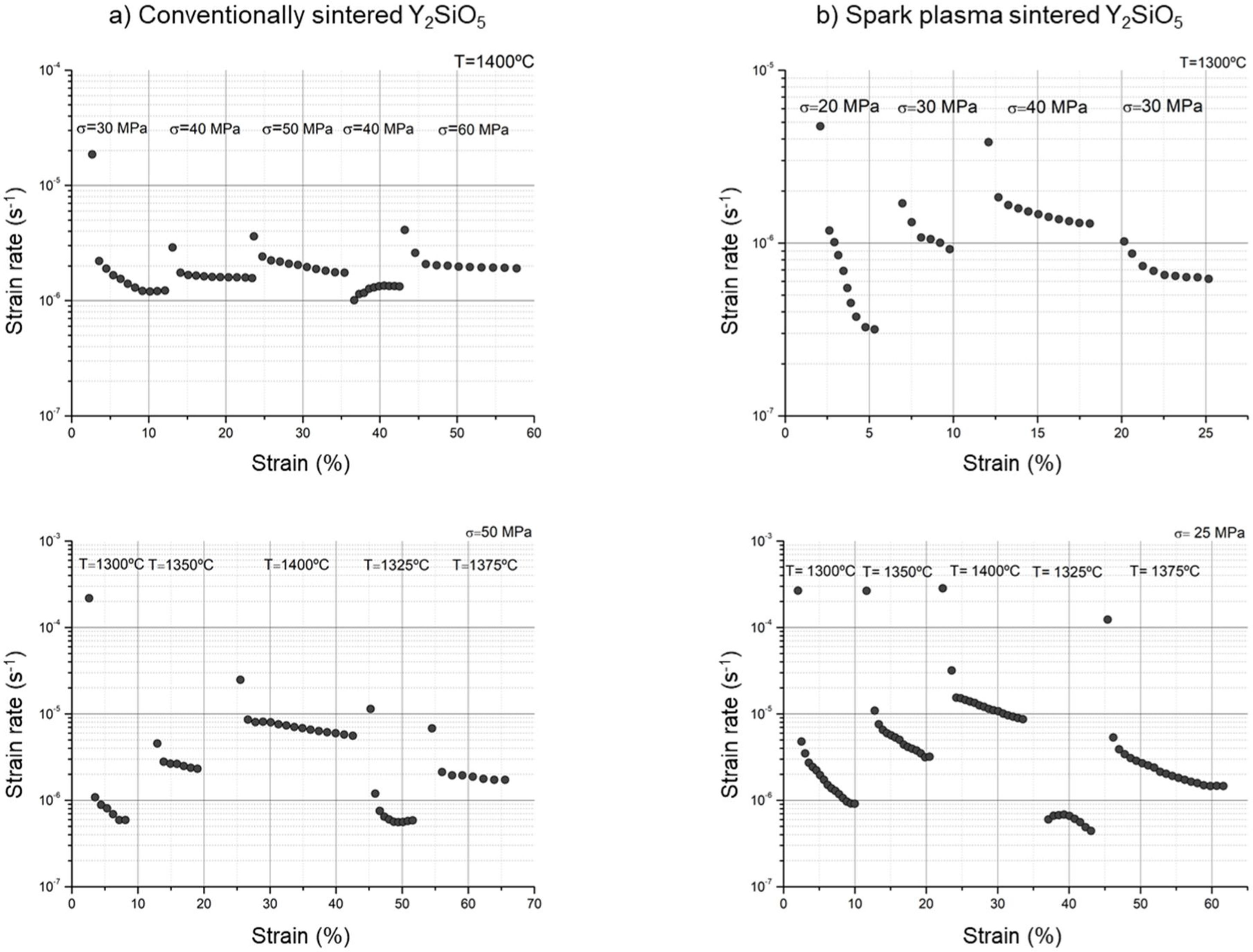
Since the creep rate is a function of stress and temperature, but also of grain size, two types of experiments were performed. In constant temperature tests the applied stress was varied in 10MPa discrete steps and the stress exponent for creep was calculated using the measured creep rates before and after the step. In constant stress experiments, the load was kept fixed, and the temperature was varied in 25°C steps. This allowed us to calculate the activation energy for creep using the creep rates before and after the temperature change. The advantage of this differential method is that creep parameters are calculated at a ‘constant microstructure’, eliminating the influence of any grain growth that could be occurring during the experiments.
Results and discussionMicrostructure and compositionThe densities of the sintered Y2SiO5 ceramics are detailed in Table 1, while the microstructure is shown in Fig. 1. In the case of Y2SiO5 prepared by solid-state reaction and conventional sintering, grains are polygonal and equiaxed, with some visible porosity (panel a). The mean grain size was 2.2±1.2μm. The spark-plasma sintered ceramic looks instead fully dense with no visible pores and shows a finer grain size of 0.9±0.4μm as determined by the linear intercept method.
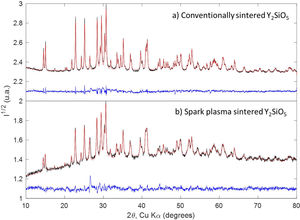
XRD patterns of the sintered Y2SiO5 ceramics are shown in Fig. 2, along with the results of Rietveld refinement. In the case of conventionally sintered Y2SiO5, 5% wt. of unreacted Y2O3 was observed, apart from monoclinic Y2SiO5. For the spark-plasma sintered ceramics, only Y2SiO5 was detected, with no other phases present in the diffractogram. The presence of Y2O3 in the conventionally sintered ceramic is probably due to the addition of LiYO2 as a sintering aid, which decomposes into Y2O3 and Li2O at high temperatures, but also due to incomplete reaction of Y2O3 and SiO2.
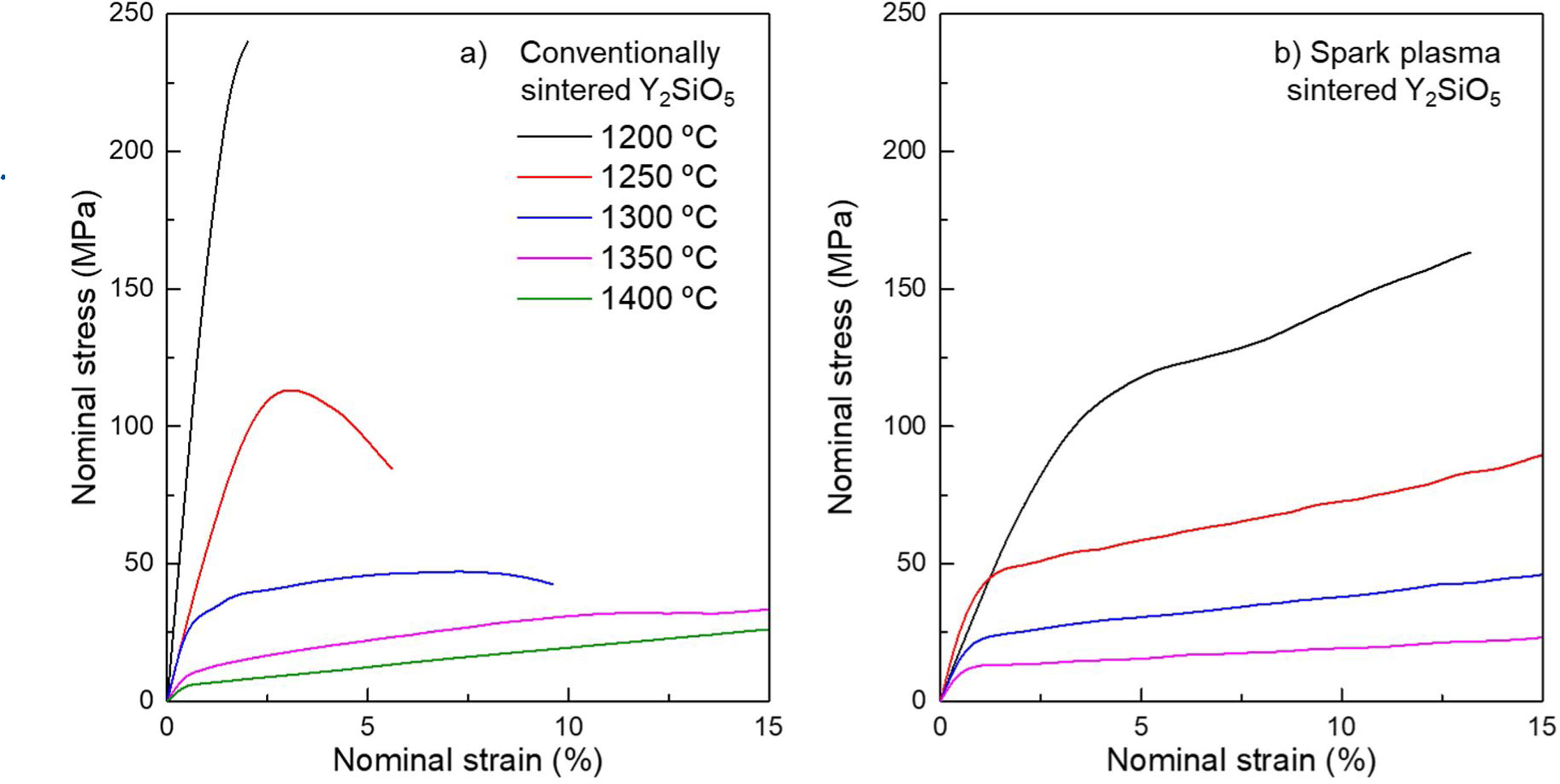
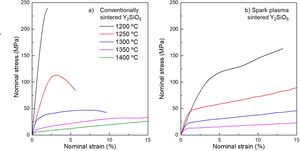
Constant strain rate testsFig. 3 shows the stress–strain curves for the Y2SiO5 ceramics at an initial strain rate of 3.2×10−6s−1 and temperatures from 1200°C to 1400°C for conventionally sintered polycrystals (panel a) and from 1200°C to 1350°C for spark-plasma sintered polycrystals (panel b). In the case of conventionally sintered Y2SiO5, the sample tested at 1200°C exhibits catastrophic failure at a stress over 230MPa after yielding, as the strain rate is too large to be accommodated via plastic deformation, resulting in the formation of microcracks that eventually coalesce resulting in the final fracture of the specimen. At 1250°C a fragile-to-ductile transition is observed, and active plasticity mechanisms are sufficient to partially accommodate the externally applied deformation rate. This accommodation is however not enough to sustain homogeneous deformation and a continuous decrease in load is observed as deformation increases, eventually resulting in gracile failure. In contrast, at temperatures 1300°C and higher, plastic deformation is sustained and high strains of ∼10% and ∼15% are observed, implying that at temperatures over 1300°C plasticity mechanisms are active and able to accommodate deformation at the applied strain rate.
An examination of the microstructure of conventionally sintered Y2SiO5 ceramics after constant strain rate deformation reveals that significant grain growth took place during the tests, as can be seen in Fig. 4. The final mean grain size after the tests is included in Table 2.
SEM micrographs of conventionally sintered Y2SiO5 ceramics after testing at temperatures from 1200°C to 1400°C, and comparison with the original as-fabricated microstructure. An increase in grain size is observed (quantitative measurements shown in Table 2).
In finer-grained, spark-plasma sintered Y2SiO5 ceramics, the stress–strain curves from constant strain-rate experiments (Fig. 3b) in all cases show sustained plasticity, and strains over 15% were reached in all cases. Investigation of the microstructure of deformed specimens showed that limited grain growth took place, in contrast with conventionally sintered Y2SiO5, but significant cavitation occurred (Fig. 5a). Despite this cavitation, the samples deformed homogeneously without significant cracking, and no macroscopic defects were observed. Fig. 5b shows a photograph of a sample tested up to strain of ɛ∼20% at 1350°C (right) and an untested specimen for comparison (left). Fig. 5c shows micrographs from a SPS sample tested at 1350°C up to 20% strain: although cavitation is evident in the first panel, the higher resolution panels show that the deformed microstructure is free from dislocations.
(a) SEM micrographs of SPS sintered Y2SiO5 ceramics after testing at temperatures from 1200°C to 1350°C, and comparison with the as-fabricated microstructure. No grain size growth is observed, however significant cavitation is present in the deformed specimens. (b) Photograph of a sample deformed up to a strain of ɛ∼20% at 1350°C (right) and comparison with an undeformed, similar specimen (left). c) TEM micrographs from a sample tested up to ɛ∼20% strain at 1350°C, where cavitation is made evident with the appearance of voids. Despite the high final strain, the microstructure appears free of dislocations.
In a typical creep experiment the strain is monitored as a function of time for a fixed applied stress and temperature. After a transient, deformation reaches a steady-state characterized by a constant strain rate, ε˙. In this regime, often called secondary or stage-II creep, the strain depends on the applied load σ and the temperature T according to the Mukherjee–Dorn–Bird equation [29]
where n is the stress exponent, Q is the activation energy for creep, p is the grain size exponent and R=3.314JK−1mol−1 is the ideal gas constant. The rest of parameters are characteristics of the material such as the shear modulus G, or its microstructure, such as the grain size d or Burger's vector modulus b.If any grain growth is taking place during the tests, then a real steady state will not be reached since an increase in grain size will lead to a reduction in strain rate according to Eq. (2). As shown in the previous section, significant grain growth was observed during the constant strain-rate experiments for the conventionally sintered ceramic, making direct application of Eq. (2) difficult. To overcome this difficulty, a differential method was employed for the determination of the stress exponent and the activation energy. In this approach, either the stress or the temperature is kept constant during each experiment while the other is varied stepwise, and the instantaneous strain rate is measured before and after each step. Then, for an experiment where the temperature is fixed, the stress exponent can be calculated as:
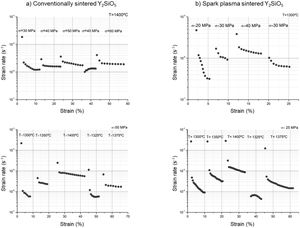
where ε˙1,σ1 and ε˙2,σ2 are the strain rate and applied stress before and after the change in load, respectively. Similarly, for a constant stress experiment where the temperature is changed step-wise, the activation energy for creep can be calculated as:Fig. 6 shows the results of the creep experiments, where lnε˙ is plotted vs the total strain ε. In all plots a true steady state is not reached. This can be due to two reasons: first, the tests were performed at a constant applied load which means that the actual stress is decreasing as deformation proceeds, since a continuous increase in the transverse section due to deformation results in a decrease in stress. Second, concurrent grain growth during tests can result in a continuous decrease in strain rate. Importantly, Fig. 6 shows that the studied ceramics can sustain deformations up to 60% in compression at 1300°C without macroscopic damage.
Table 3 shows the calculated stress exponents and activation energies for both ceramics, as calculated from the creep curves of Fig. 6.
The marked difference in stress exponent between the two ceramics is another indication that the two Y2SiO5 deform plastically via different mechanisms. A stress exponent n∼1 is normally indicative of diffusional creep, either through the bulk or the grain boundaries, whereas a stress exponent of n∼2 is normally found in superplastic ceramics and attributed to a grain boundary sliding deformation mechanism accommodated by diffusion [30].
The activation energies are similar for both ceramics when the standard deviation is considered, indicating that although the deformation mechanisms differ, the accommodation mechanism is similar and that the rate-controlling species for diffusion could be the same. Calculations performed by Liu et al. [31] showed that that oxygen vacancy is the predominant vacancy species in Y2SiO5 and calculated an activation energy of oxygen self-diffusion of 430–480kJmol−1, which is in the range of our measured values, allowing us to conclude that creep is accommodated by bulk self-diffusion and controlled by oxygen vacancies.
Despite the small differences in grain size, our results show that the two ceramics deform by different mechanisms, evidenced by the transition from a stress exponent n=2 to n=1 when the initial grain size changes from ∼0.9μm to ∼2.4μm. The transition to a stress exponent of n=2 when the grain size decreases below about 1μm has been reported for yttria stabilized zirconia with grain sizes ranging from 0.3 to 17μm [32] although there is still no simple explanation for this effect. A similar transition has been shown in the case of La9.33Si6O26 ceramics processed by conventional sintering (d=1.1μm, n=1) and SPS (d=0.2μm, n=2) [28].
It has been shown that due to the rapid heating and cooling, SPS can lead to the apparition of residual stress or result in metastable microstructures that can affect the room temperature properties of the resulting ceramic. One paper found differences in the wear behavior of SiC nanoceramics processed by SPS after a gentle annealing at 1200°C for 12h in vacuum [33], while another reported large differences in both room-temperature bending strength and creep for SPS alumina polycrystals after annealing for 5h in air at 1000°C [34]. Both papers attribute this difference to the presence of residual stresses in the as-processed samples that are relaxed after annealing. In our case, and due to the high temperatures employed, the slow heating rates and 1h of dwell time before the start of each test should be enough to relieve any residual stress in the samples. If residual stresses are accommodated by mass transport and ultimately diffusion, for our determined activation energy of ∼500kJ and assuming an Arrhenius-type behavior, a 1h annealing at 1300°C is equivalent to ∼12h at 1200°C, the SPS peak temperature and thus any residual stresses will have relaxed before the start of each test.
ConclusionsClose to fully dense Y2SiO5 polycrystals were prepared by two different synthesis and sintering methods, to obtain ceramics suitable for high-temperature compression experiments. In the case of conventionally sintered ceramics, densities of ∼92% were achieved with a mean grain size of 2.2μm, whereas spark-plasma sintered ceramics showed a density of ∼95% and a mean grain size of 0.9μm. Despite the small differences in microstructure, both ceramics showed markedly different mechanical properties. The conventionally sintered ceramic exhibited a brittle to ductile transition at ∼1250°C as deformation mechanisms became active to accommodate deformation, whereas the finer-grained ceramic showed extensive deformation and close to superplastic behavior in the whole temperature range studied. Microstructural investigation showed cavitation in the spark-plasma sintered ceramic without grain coarsening, while the conventionally sintered ceramic showed appreciable grain growth. Creep experiments confirmed the difference between the two microstructures: the larger-grained ceramic showed a stress exponent of n∼1 indicative of diffusional creep while the finer-grained ceramic exhibited a stress exponent of n∼2.5, compatible with grain boundary sliding. Activation energy was similar in both cases and compatible with that previously reported for oxygen self-diffusion.
R. Cabezas-Rodriguez acknowledges a travel grant from the University of Seville (PP2015-4234) to École CentraleSupélec (France). X-ray diffraction and electron microscopy was performed at the CITIUS central services of the University of Seville (Spain). We are thankful to B. Lacroix for his help with TEM imaging.
The authors thank Prof. Víctor M. Orera, to whose memory this work is dedicated, for his many contributions to the field and for always being a source of inspiration.