La estadística es la disciplina interesada en la organización y resumen de datos, para obtener conclusiones acerca de las características de un conjunto de personas u objetos, cuando solo una porción está disponible para su estudio. La bioestadística es la rama de la estadística que se ocupa de los problemas planteados dentro de la ciencia de la vida, como la biología o la medicina1. Médicos, enfermeras, kinesiólogos, especialistas en salud pública, entre otros, necesitan conocer los principios que guían la aplicación de los métodos estadísticos a los temas propios de sus respectivas áreas de conocimiento, porque es el método objetivo, racional y matemático a través del cual, una hipótesis científica puede ser comprobada2. Es por eso, que para facilitar su estudio, se ha dividido en cuatro funciones: el diseño muestral, el cálculo de tamaño muestral, la estadística descriptiva y la estadística analítica o inferencial. Considerando que la investigación clínica se realiza en una muestra que debe representar la población de estudio, es necesario que los datos sean matemáticamente analizados, utilizando las pruebas estadísticas apropiadas, para que se puedan extraer conclusiones científicamente válidas. Tan relevante es la bioestadística, que la evidencia en salud está construida en base a ésta.
Actualmente, existen numerosos libros y artículos sobre esta disciplina, por lo tanto, se preguntarán ¿por qué escribir más de lo mismo? Porque aún para los profesionales de la salud, la bioestadística sigue siendo un área que cuesta aterrizar al contexto clínico, cuando se está planificando un estudio de investigación o se analiza un paper porque surgen preguntas sobre sus pacientes. Por esa razón, el objetivo de este artículo es revisar los conceptos y elementos básicos de la bioestadística que se usan en la investigación clínica, con la perspectiva de la estadística aplicada y la óptica de un clínico.
Se espera que al término de su lectura, el artículo les entregue un enfoque más claro y ordenado para abordar las cuatro funciones de la bioestadística y su cumplimiento en el proceso de la investigación.
Statistics is the discipline interested in the organization and summary of data, to obtain conclusions about the characteristics of a group of people or objects, when only a portion is available for study. Biostatistics is the area of statistics that deals with the problems in science of life, such as biology or medicine1. Physicians, nurses, kinesiologists, public health specialists, among others, need to know the principles that guide the statistical methods to the topics of their respective areas of knowledge, because it is the objective, rational and mathematical method through which, a scientific hypothesis can be proven2. That is why, to facilitate the study of statisitics, it has been divided into four functions; the sample design, the sample size calculation, the descriptive statistics and the analytical or inferential statistics. Considering clinical research is carried out on a sample that should represent the study population, it is necessary, the data be mathematically analyzed; using the appropriate statistical tests, so scientifically valid conclusions can be drawn. So relevant is biostatistics, that evidence based medicine is built on it.
Currently, there are numerous books and papers on this discipline, therefore, why write more of the same? Because, even for health professionals, biostatistics is still an area that costs to apply in the clinical context, when they are planning a research study or analyzing a paper because they have questions about their patients. For this reason, the aim of the article is to review the concepts and basic elements of biostatistics frequently used in clinical research, with the perspective of applied statistics and the clinician optics. It is expected that at the end of its reading, the article will provide a clearer and more orderly approach to address the four functions of biostatistics and its fulfillment in the research process.
“La variabilidad es quizás lo único constante en nuestro mundo”. Cobo y cols. 2007 “Toda Ciencia es medición, toda medición es estadística”. Herman von Helhmotz (1821-1894)
La palabra estadística proviene del latín status: modo de pararse, posición. En el lenguaje cotidiano se habla de estadística en dos sentidos, uno es para referirse a un conjunto determinado de datos, por ejemplo, a la estadística de población o estadísticas de ventas.
El otro sentido se refiere a una disciplina matemática, donde la estadística matemática es una de las áreas de la ciencia matemática. Al mismo tiempo, la estadística se estudia desde el punto de vista práctico, desde su aplicación, por ejemplo, la estadística aplicada a la administración y economía. Otra de las áreas de la estadística aplicada, es su uso en la ciencia biológica y las disciplinas relacionadas con la medicina y la salud. A esta se le llama bioestadística1.
Se han publicado varias definiciones al respecto, tales como la definición clásica de Croxton y Cowen3 dice: “La estadística es el método científico que se utiliza para recolectar, elaborar, analizar e interpretar datos sobre características susceptibles de ser expresadas numéricamente de un conjunto de hechos, personas o cosas”.
Otra definición de Clifford y Taylor1: “La estadística es la disciplina interesada en la organización y resumen de datos, para obtención de conclusiones acerca de las características de un conjunto de personas u objetos cuando solo una porción está disponible para su estudio”.
La estadística es un conjunto de técnicas para el análisis de los datos. De esto se desprenden dos componentes principales de esta disciplina: Datos y análisis.
Los datos son la materia prima de la estadística. Los datos salen de las mediciones o también llamadas observaciones. Al mismo tiempo, las técnicas de análisis estadísticas permiten que los datos se conviertan en información útil4. Ambos componentes son fundamentales y uno necesita del otro para que los resultados sean útiles para responder la pregunta de investigación.
Si existen errores en los datos, independiente que las técnicas de análisis estadísticos sean las correctas, los resultados serán erróneos; si por el contrario, los datos han sido correctamente extraídos con precisión y exactitud, pero las técnicas de análisis son inadecuadas, igualmente los resultados serán espurios.
Según Mainland5, la estadística es el método científico que se ocupa del estudio de la variación; y según Cobo y cols., La variabilidad es quizás lo único constante en nuestro mundo6.
Ahora bien ¿Cómo predecir la variabilidad entre los diferentes casos clínicos? El profesional sanitario construye su ojo clínico a base de horas de trabajo. La estadística le ofrece conceptos que pueden facilitar este aprendizaje. Al mismo tiempo, es importante tener presente que los métodos estadísticos y sus resultados no pretenden ser verdades absolutas, puesto que la medicina no es exacta, solo es posible calcular las probabilidades que ocurran los eventos en salud. De hecho, el concepto principal de la estadística es la variabilidad, pero el conocer cómo medirla y modelarla comienza a ser una idea positiva y de ayuda para su aplicación en salud. La estadística aporta teoremas que conectan la variabilidad e independencia con la información que se recolecta de los sujetos o unidad muestrales6.
En consecuencia, se podría definir que la bioestadística es el método objetivo, racional y matemático a través del cual una hipótesis científica puede ser comprobada.
Las estadísticas de salud son todos aquellos datos numéricos debidamente capturados, validados, elaborados analizados e interpretados que se requieren para las acciones de salud.
Las estadísticas de salud se pueden agrupar en7:
- 1.
Estadística de poblaciones: estadísticas demográficas.
- 2.
De hechos biológicos que tiene trascendencia sanitaria, como los nacimientos y defunciones: estadísticas vitales.
- 3.
De la enfermedad, que se intenta prevenir y tratar: estadísticas de morbilidad.
- 4.
De los medios tanto específicos como inespecíficos para proteger, fomentar, detectar y recuperar la salud: estadísticas de recursos.
- 5.
De las acciones e intervenciones, que desarrollan los recursos básicos para la evaluación: estadísticas de servicios.
La estadística en salud depende de los datos y de su análisis, por lo tanto, es esencial conocer la metodología para la correcta recolección de los datos y comprender la estadística para un correcto análisis de éstos. En consecuencia y dada su relevancia, el objetivo de este artículo es entregar algunas nociones básicas sobre bioestadística aplicada en la investigación y cómo a través de ésta, es factible responder la pregunta de investigación.
2. CONCEPTOS BÁSICOSAntes de revisar y presentar los conceptos y elementos básicos de la bioestadística, que se aplican más frecuentemente en la investigación clínica, se explicarán algunas definiciones básicas más usadas.
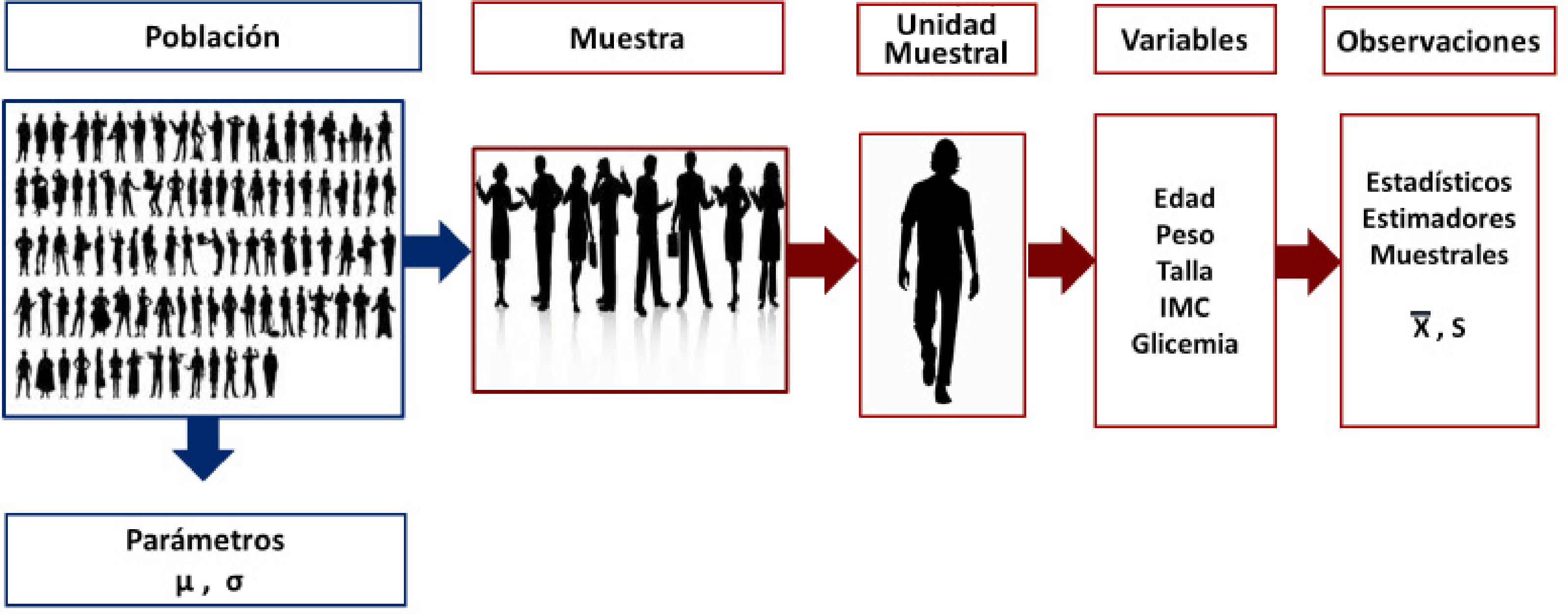
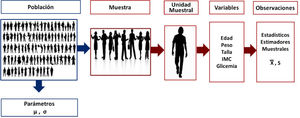
Parámetro: Es cualquier número resumen de los elementos de una población1. Otra definición de Villarroel LA 2018, el parámetro es una función de los datos calculada en la población8
Este término muchas veces es incorrectamente utilizado y se habla de los parámetros del estudio, cuando en realidad no lo son, porque lo que se obtiene, es un número resumen extraído desde una muestra, no de la población general. A esta medida resumen de los datos de una muestra se le llama estadístico. Los parámetros se denotan con letra griega, tales como μ, que es la media de una variable que ha sido calculada en la población total; σ, es la varianza de una variable calculada en la población total1. Como la mayoría de la investigación se realiza en una muestra, no es factible obtener un parámetro, solo es posible calcular una estimador, a través de los estadísticos.
Estadísticos: Es cualquier número resumen de una muestra. También se le puede llamar parámetro estimado, que es el término correcto cuando se habla de un número resumen que deriva de una muestra. Como es solo un estimador del parámetro, se denota con letras en latín; X es la media de una muestra; S, es la varianza de una muestra1,9.
El estimador debiera cumplir con las propiedades de insesgamiento, que la esperanza sea casi igual al valor observado, que sea eficiente (preciso, que tenga una varianza cercana a cero) y que sea robusto, es decir que ese número resumen, sea capaz de representar a toda la muestra.
Observar: Es medir. Lo observado es lo medido. Las observaciones son las mediciones que se realizan en las unidades muestrales.
Unidad de análisis o unidad muestral: Es el objeto con la característica de interés que será observado o que será medido, pueden ser personas, cortes histológicos, crecimiento de colonias, entre otros.
Atributo: Es la característica de la unidad de análisis que se va a observar.
Por ejemplo: Si se desea observar antropométricamente al Recién Nacido (RN), se deben consignar los atributos a medir: Edad gestacional (EG), peso nacimiento (PN) y talla de nacimiento (TN).
Variable: Es cualquier característica que tome dos o más valores en una población.
Cuando los atributos ya han sido medidos, reciben el nombre de variables. Por ejemplo: RN n°1: EG: 39 semanas PN: 3250 grs. TN: 50cms. Se llaman variables, porque cambia entre cada unidad de análisis.
Variable aleatoria: Son aquellos atributos que han sido medidos en un conjunto de individuos de la población que conforman una muestra aleatoria y que no se puede anticipar el resultado (Figura 1).
3. PLANIFICACIÓN ESTADÍSTICACuando se escribe un proyecto de investigación, se diseña la metodología del estudio y dentro de ésta, es indispensable diseñar la planificación estadística (PE). Debe estar enfocada en cumplir cada uno de los objetivos específicos y el objetivo general y con ello responder la pregunta de investigación. La PE consiste en:
- I.
Definir y diseñar el método de selección de la muestra, esto se llama diseño muestral.
- II.
Definir el número de elementos que conformará la muestra, esto se llama cálculo de tamaño muestral.
- III.
Definir las variables: El tipo variables, la escala de medición y la unidad de medida si es que aplica.
- IV.
Plan de tabulación de la base de datos, descripción y análisis de la información recolectada. Se definen las formas de presentar y analizar la información recolectada7.
La población así también llamada universo de estudio, es el conjunto total de personas u objetos que tienen una característica en común de interés para un estudio. No obstante, estudiar toda la población tiene algunos inconvenientes: es difícil poder ejecutar una investigación en toda la población estudio porque es muy caro y demoraría mucho tiempo reclutar y medirlas a todos. Por lo tanto, se debe estudiar en una muestra.
Muestra: Es un subconjunto de individuos o elementos de una población definida que cumple con ciertas propiedades comunes. Para que el estudio en una muestra permita extrapolar los resultados a la población de estudio, es necesario que cumpla con las siguientes exigencias:
1. Representativa de la población de estudio o población blanco: Implica que, para que los resultados del estudio tengan validez interna y externa, la muestra debe ser representativa de la población blanco.
Si la muestra no es representativa de la población de donde procede, todos los cálculos que se hagan serán válidos solo para la muestra, sin posibilidad de extrapolar estos resultados a los individuos que no fueron incluidos en ella8.
Es decir, todos los subgrupos que componen la población blanco, debieran estar en la muestra, respetando el peso proporcional o ponderado que cada uno tiene en la población de estudio. Al elegir los elementos de la muestra siguiendo una tendencia o preferencia por unos más que otros, el grupo preferencial va a ser cuantitativamente mayor. Si es así, la muestra no será fiel representante de la población de estudio y los resultados y conclusiones estarán sesgados, junto a la validez interna y externa que será afectada.
2. Selección aleatoria: Significa que los sujetos de la población blanco deben ser escogidos al azar, es decir, todos los individuos o elementos de la población blanco tienen que tener la misma probabilidad de ser seleccionados en la muestra. Eso significa, que todas las personas u objetos de la población deben tener una probabilidad mayor a cero y menor a uno de estar presente en la muestra. El método de selección de la muestra se llama diseño muestral. Existen diferentes tipos de diseño muestral, si es aleatorio se le llama probabilístico, si no es aleatorio, es no probabilístico.
3. Tamaño mínimo adecuado: Es el número de individuos necesarios y seleccionados aleatoriamente, que debe contener la muestra, para obtener estimaciones que representen los valores reales del parámetro de la población de estudio. Es por esto, que se debe realizar un cálculo de tamaño muestral9.
1. Diseño muestral
La selección de la muestra aleatoria es indispensable que para la obtención de resultados válidos.
Muestra aleatoria: Es una selección al azar de los individuos que componen la muestra. Existen diferentes tipos de métodos de selección de la muestra6,8.
1.1. Muestreo probabilístico
1.1.1. Aleatorio Simple: Se asume que la población es homogénea y que todos los elementos de la población tienen la misma probabilidad de elegidos en la muestra. Se debe tener un registro de todos los sujetos de la población blanco (rut, n° ficha clínica, u otros). La selección se puede hacer con métodos simples (una bolsa de papeles), tablas de n° aleatorios o generación de n° aleatorios por computador.
Ventajas: técnica sencilla.
Desventajas: la muestra puede quedar desequilibrada, si no se toman en cuenta los subgrupos y su peso ponderado o proporcional respecto a la población de Estudio.
1.1.2. Muestreo Estratificado: Este diseño muestral tiene por objetivo evitar que, por azar, algún grupo esté menos representado que otro. Se asume que la población es heterogénea y que existen subgrupos, y es por eso, que se agrupa la población en unidades homogéneas que se llaman Estratos. Posteriormente se calcula el peso ponderado de cada estrato, para determinar el tamaño de la muestra en cada uno. Por último, mediante muestreo aleatorio simple, se obtiene una muestra aleatoria de cada estrato para obtener la parte proporcional de la muestra.
Ventajas:
- •
Previene que la muestra quede desequilibrada respecto a la representación de cada subgrupo o estrato.
- •
Disminuye la variabilidad dentro de los estratos
- •
Permite resultados más precisos.
Desventajas:
- •
Complica un poco más el diseño muestral.
- •
Si existen muchos estratos, puede reducir el n muestral para cada estrato.
- •
No se aconseja más de 8 -10 estratos.
- •
Necesita más tamaño muestral.
1.1.3. Muestreo Sistemático: Se usa cuando los elementos de la población están ordenados. En este caso se elige el primer individuo al azar y el resto viene condicionado por aquel. Hay que comprobar que la característica que se estudia no tenga una periodicidad que coincida con la del muestreo.
Ventajas:
- •
Obtiene buenas propiedades de representatividad, similares a la de un muestreo aleatorio simple o incluso superiores, pero de forma más rápida y simple, al evitar la necesidad de generar tantos números aleatorios como individuos en la muestra.
- •
Respecto al muestreo aleatorio, el muestreo sistemático puede garantizar una selección perfectamente equitativa de la población. Esto puede ser de utilidad si se distinguen grupos dentro de la población blanco y formar grupos homogéneos, lo que podría evitar la necesidad de usar estratos.
Desventajas:
- •
Existe la posibilidad de que el orden en que se han listado los candidatos a la muestra tenga algún tipo de periodicidad oculta que coincida con el intervalo escogido para generar la muestra sistemática. En este caso, se podría generar una muestra que contenga un sesgo de selección.
1.1.4. Muestreo por Conglomerado: Se usa cuando el muestreo aleatorio simple es demasiado caro, por la gran magnitud de población y tampoco se tiene un listado de los individuos que la componen.
Un conglomerado es una división de la población donde interesa que los individuos al interior sean heterogéneos, que haya diversidad al interior del conglomerado, pero los conglomerados entre sí sean homogéneos. Se toma una muestra aleatoria de conglomerados y luego se selecciona al azar los individuos de cada conglomerado seleccionado.
Ventajas
- •
Útil para estudios epidemiológicos que desea abarcar poblaciones de diferentes regiones
- •
Útil para grandes “n” muestrales
- •
Útil para estudios ecológicos
- •
Útil para estudios en diferentes locaciones en terreno
Desventajas
- •
Exige un conocimiento previo de las zonas de estudio
- •
Necesita información sobre las áreas o lugares que se desea muestrear
- •
Implica uso de estratificación y ponderación de los grupos
1.2. Muestreo no probabilístico
1.2.1. No probabilístico o sin asignación aleatoria: Método de muestreo que no se basa en probabilidades, es un muestreo por conveniencia o de cuotas. Es elegido. Es población con características muy específicas y se usa porque hay facilidad de acceso para los investigadores. Hay sesgo de selección y es el muestreo más frecuentemente utilizado.
1.2.2. De asignación aleatoria: A pesar de que la muestra no tuvo selección aleatoria, la asignación de la intervención es a través de métodos aleatorios. Esto permite que los grupos receptores de las exposiciones sean lo más similares posibles y que sean comparables. Por lo tanto, un muestreo no probabilístico consecutivo por conveniencia, con asignación aleatoria, con intervención y medición enmascarada, con largo periodo de reclutamiento para que incluya variaciones estacionales u otros cambios temporales y con más de un centro reclutador, es el escenario ideal, en el caso de un diseño muestral no probabilístico. Este es el diseño muestral que se usa en los ensayos clínicos controlados aleatorizados doble ciego multicéntricos9,15.
Ventajas:
- •
Ventaja principal es la conveniencia para el acceso a las unidades muestrales
- •
Simple
- •
Económico
- •
Rápido
Desventajas:
- •
El principal defecto, la falta de representatividad y validez externa.
- •
Imposibilidad de hacer generalizaciones y aseveraciones estadísticas sobre los resultados.
- •
Riesgo de incurrir en sesgos debido al criterio de muestreo empleado.
- •
En el peor de los casos, el tiempo de muestra conveniente puede presentar un sesgo sistemático respecto al total de la población, lo que produciría resultados distorsionados.
Otra de las exigencias que debe tener una muestra es que tenga el tamaño mínimo adecuado para que represente cuantitativamente a la población de estudio o blanco. No obstante, ¿cómo determinar el número de elementos que necesita la muestra para cumplir con el tamaño mínimo adecuado? ¿para qué tipo de estudio necesito una muestra?
En investigación clínica se realiza cálculo de tamaño muestral (Ctmu) para varios objetivos y existen diferentes métodos, según el objetivo del estudio. No obstante, los más usados son para estimar un parámetro o para probar una hipótesis y es lo que explicaré a continuación.
2.1 Estimar un parámetro10,11El objetivo del Ctmu, es obtener la estimación de un parámetro, o sea obtener un estadígrafo representativo de la población de estudio y que responde la siguiente pregunta: ¿Cuántas unidades de análisis es necesario estudiar para poder estimar el valor de una variable con el grado de confianza deseado y que represente al parámetro de la población de estudio? Para ello, el Ctmu exige supuestos que se muestran en la figura 2.
2.1.1 Variabilidad del parámetro o la probabilidad del evento que se desea estimar
Cuando se desea estimar una media, se necesita la varianza, a mayor variabilidad tiene un atributo, se necesitará un mayor número de medidas, por lo tanto, una muestra más grande. Si no se conoce la variabilidad del parámetro, puede obtenerse, a partir de la evidencia de estudios análogos, o a partir de los resultados de un estudio piloto o en última instancia a partir de datos propios observados en la práctica clínica. Si el parámetro a estimar es una variable cualitativa, se usa la probabilidad del evento (P).
2.1.2. Precisión de la estimación del “parámetro”
Es la amplitud del intervalo de confianza. Cuanto más precisa sea la estimación, más estrecho deberá ser el intervalo y más sujetos deberán ser estudiados. Debe fijarse previamente la precisión de la estimación del “parámetro”. La amplitud del IC dependerá del objetivo del estudio, si necesita gran precisión o solo una aproximación. Se denota con una “d” o “I”. Puedes ir desde 0.1 – 0.010
2.1.3. Nivel de confianza
Por convención se fija en 95% corresponde a un valor de error α de un 5% en que el “parámetro estimado” se equivoque por azar solo en un 5%.
Ctmu para estimar una media:
n=Zα2S2/I2 Aquí se asume una distribución Gaussiana.
Ctmu para estimar una proporción:
n=Zα2(p q)/I2 Aquí se asume una distribución Bernoulli.
2. Para comparar proporciones8,10,11
El objetivo del Ctmu, es obtener el tamaño muestral necesario que permita detectar estadísticamente una magnitud de diferencia entre dos grupos, en el supuesto que realmente exista. Al igual que para estimación de parámetros, este Ctmu requiere supuestos, que se deben fijar a priori y que se enumeran en la figura 3.
En toda investigación que desea comprobar una hipótesis, es necesario evitar los errores en el número y la calidad de las mediciones. Es decir, conseguir la máxima exactitud al medir, lo significa, procurar que exista validez en la medición y prevenir el error aleatorio.
¿Qué es la Validez? Es que se mida lo que se desea medir, sin sesgo. ¿Qué el sesgo? Es el error sistemático prevenible, que se comente al efectuar las mediciones y que puede ocurrir por un defecto en el observador (quien mide), en el instrumento de medición, o en el observado (sujeto que se mide). El sesgo es prevenible con una correcta selección de los sujetos, una correcto proceso de medición y recolección de la información (sesgo de información) y controlando las variables de confusión. El sesgo se previene y controla a través de la metodología de investigación del estudio, que finalmente es el modo de diseñar, ejecutar y analizar el estudio10,11.
¿Qué es el error aleatorio? También se le puede llamar accidental o error de precisión y es debido a pequeñas causas que son imposibles de controlar por el investigador. Uno de ellos es el hecho de estudian en una muestra para sacar conclusiones que se apliquen a toda la población y eso se llama error de muestreo2.
Supuestos del cálculo de tamaño muestral para comparar proporciones
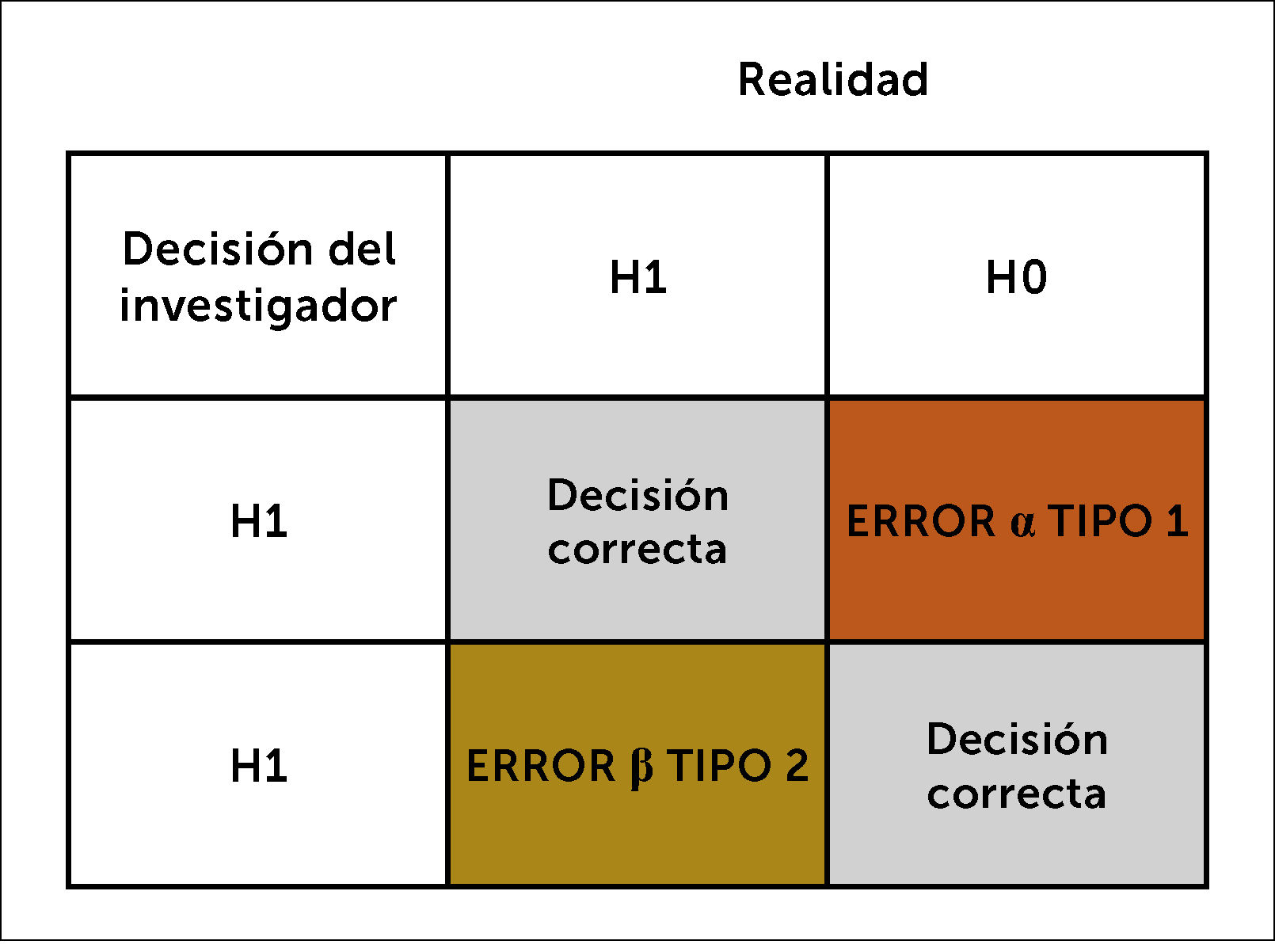
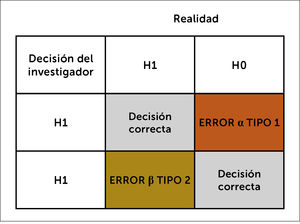
2.1. Error tipo 1 o α: Es el error aleatorio y que se refleja en el error tipo 1 o α. Éste se debe fijar a priori cuando se realiza un cálculo de tamaño muestral. ¿Cuánto error aleatorio el investigador está dispuesto a aceptar?
Se define como el error que comete el investigador al rechazar la hipótesis nula (HO), siendo esta verdadera, dicho de otra forma, es rechazar la hipótesis nula (H0) cuando es cierta. Concluir que si existe asociación entre una variable independiente (X) y una variable dependiente (Y) cuando realmente NO existe. Convencionalmente se ha fijado en un error α de 5%, no obstante, eso depende del riesgo y el costo que podría implicar equivocarse. Por ejemplo, en los estudios de terapia, donde se está evaluando la eficacia de un producto farmacéutico, se puede fijar un error alfa más pequeño, como 1%. Un error α de 5% significa que si se hiciera 100 veces el mismo experimento, solo en 5 ocasiones los resultados serían por error aleatorio y 95 veces los resultados serían con el estimador verdadero. En consecuencia, se realiza un cálculo de tamaño muestral, con el fin que el número de unidades muestrales sea el estadísticamente necesario para prevenir este error.
Valor P
Al fijar el error α, se fija el valor P. Porque el valor p es el valor de la probabilidad de cometer error α, es decir cometer error aleatorio. El valor p es la probabilidad de “caer” en la zona de rechazo: esto es descartar H0 siendo cierta. Para decirlo en términos más simples, hasta qué punto el resultado observado, es decir medido, es probabilísticamente compatible con la hipótesis planteada, o sea H112,13.
El valor p es equivalente al valor de significancia α, con la diferencia de que el valor p se calcula a partir de una muestra a posteriori mientras que el valor α se fija antes de ejecutar el estudio a priori, cuando se realiza el cálculo de tamaño muestral6. Por lo tanto, el valor p no tiene relevancia si previamente no se ha realizado un cálculo de tamaño muestral, donde se fija a priori el valor α y la magnitud de diferencia que se desea estadísticamente probar.
Por ejemplo, un valor p=0.01, quiere decir que la probabilidad que el resultado del estudio sea error aleatorio α, es de 1%. O un valor p=0.001 quiere decir que la probabilidad que el resultado del estudio por error, es de 0.1%, o que se haya cometido un error α aleatorio, es de 0.1%.
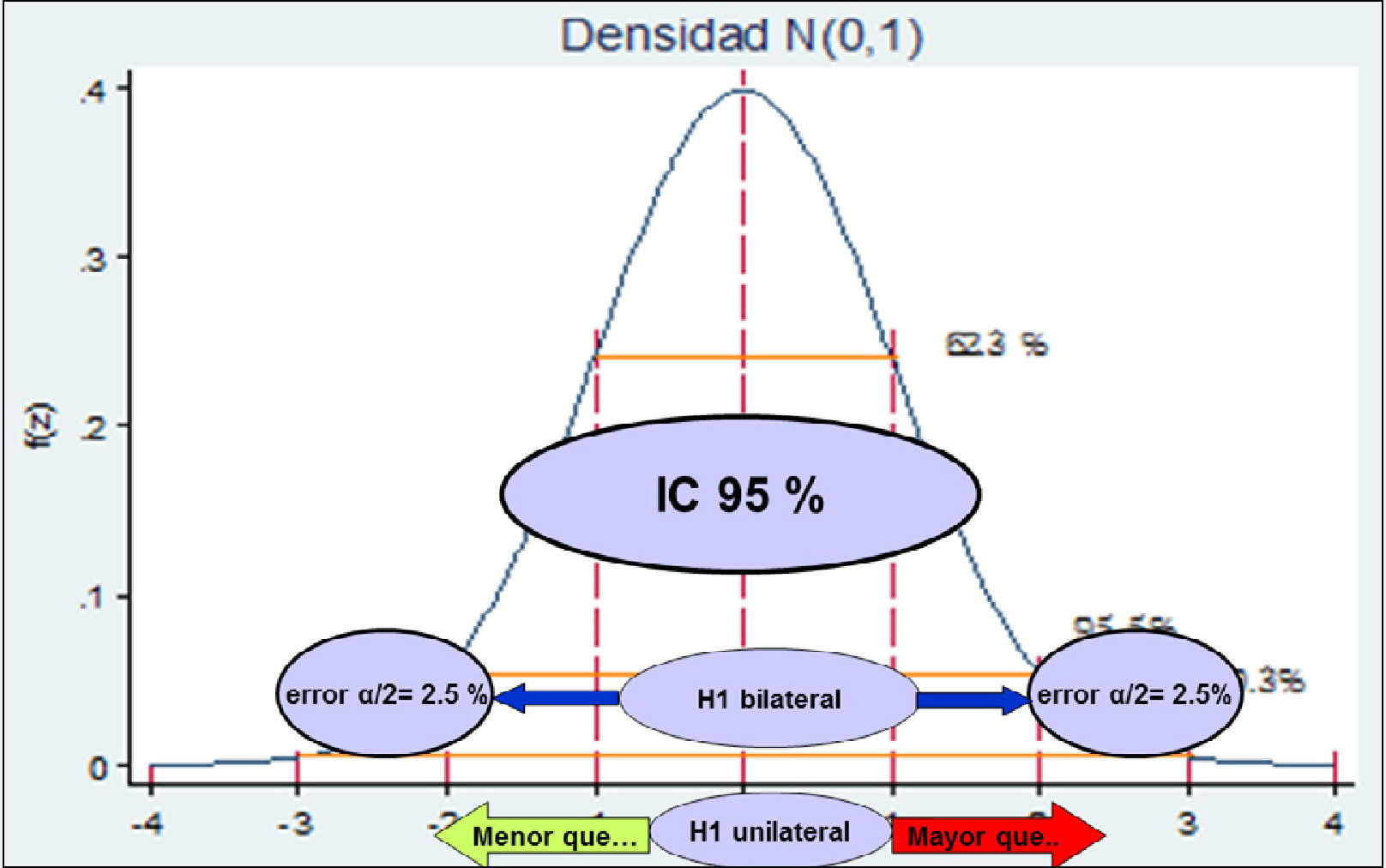
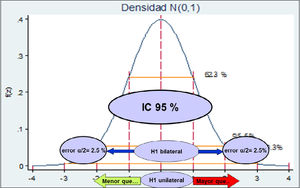
El valor p se fija a priori y depende del nivel de confianza que fije el estudio. El nivel de confianza es la probabilidad que el verdadero valor del parámetro se encuentre dentro del intervalo encontrado en el estudio. Esto se llama también, intervalo de confianza (IC). Si se exige un IC95%, el valor p de significación estadística será<0.05
Desde el IC sale el error α. Ahora bien, si la hipótesis es a dos colas o bilateral (hay diferencia), el error α/2 será el que se fije, pero si la hipótesis es unilateral (hay una diferencia mayor o menor), el error será α.
No obstante, es necesario considerar que el valor p mide la fuerza de la evidencia estadística de un estudio realizado en una muestra, pero no mide la fuerza de la asociación. Ahora bien, cuanto menor sea el valor p, mayor fuerza tienen las evidencias del estudio y menor probabilidad de rechazar la hipótesis nula (H0), siendo esta cierta. Sin embargo, es indispensable, que se entiendan dos puntos:
- •
La significación estadística, no necesariamente implica que sea clínicamente significativo para el paciente. Si se encuentra una significación estadística, pero finalmente no cambia el escenario para el paciente o no cambia el escenario en el tratamiento o cuidado, esa diferencia significativa que se encontró, no tiene mayor relevancia clínica.
- •
Si el estudio no alcanza el tamaño muestral calculado, la fuerza estadística pierde potencia y el valor p que derive de las comparaciones, tendrá que mirarse con cautela, porque la significación estadística se fijó para un determinado tamaño muestral.
- •
Un valor p, derivado de un estudio que no ha tenido un cálculo de tamaño muestral para probar una diferencia, no tiene mayor validez. Porque no hay certeza de donde proviene ese valor p<0.05.
2.2. Error tipo II o β: Es aceptar HO cuando no es cierta. Concluir que no existe asociación entre una variable independiente (X) y una variable dependiente (Y) cuando realmente SI existe. Se define como el error que comete el Investigador al no rechazar la hipótesis nula, siendo esta falsa. β representa la probabilidad de un resultado falso negativo. El complemento 1- β representa la probabilidad de observar en la muestra una determinada diferencia o efecto y es a lo que se llama el poder estadístico o potencia del estudio.
La magnitud del error β es otro de los supuestos que se debe fijar para el cálculo de tamaño muestral. Por convención, generalmente se usa el error β de 20%, lo que da una potencia del estudio de 80%, pero esto dependerá de los intereses y exigencias que se ponga el investigador y de la potencia que se quiera dar al estudio. Mientras mayor el error, menor potencia, se disminuye la credibilidad de los resultados. Los errores α y β nunca se pueden evitar en un 100%, sin embargo, se puede reducir su probabilidad, aumentando el tamaño muestral y con un adecuado diseño del estudio. Figura 4.
2.3. Magnitud de diferencia: La magnitud de la diferencia que se postula encontrar tiene una gran influencia en el tamaño de la muestra. Se debe definir la mínima magnitud de diferencia que se desea detectar y que sea de relevancia clínica para el paciente, por lo tanto, debe fijarse en términos realistas. Cuando la magnitud de diferencia es muy amplia se detectará más fácilmente y requerirá un menor tamaño muestral. Cuando la magnitud de diferencia es muy estrecha, será más difícil detectarla y requerirá un mayor tamaño muestral.
2.4. Tipo de hipótesis: Si es bilateral o a dos colas, en que postula que existe diferencia o que no existe diferencia.
Si es unilateral o a una cola, en que postula que existe una diferencia mayor o menor que. Figura 4
2.5 La probabilidad del efecto estándar (P1) y la probabilidad del efecto que se propone (P2).
Dependiendo del error alfa y el tipo de hipótesis, derivarán el valor p, que será analizado en un texto más adelante. Figura 5.
¿Qué implica un cálculo de tamaño muestral incorrecto?
a. Un exceso de tamaño muestral: Encarece el estudio. No es ético someter a más pacientes de lo necesario a la intervención o la vulneración de los datos.
b. Un insuficiente tamaño muestral, el “parámetro estimado” será poco preciso. O si se desea probar una hipótesis, una muestra con escaso tamaño, será incapaz de detectar la diferencia entre los grupos de estudio y se llegará a una conclusión errónea que no existe diferencia estadísticamente significativa, pero no porque realmente no hubo diferencia significativa, sino porque no se alcanzó un número necesario de magnitud de diferencia para que ésta fuera significativa.
En consecuencia, se realiza el cálculo de tamaño muestral, para que el investigador sepa el número mínimo necesario de unidades muestrales que debe estudiar, con el fin que los resultados estadísticos sean creíbles y permitan estimar un parámetro extrapolable a la población de estudio. En el caso de querer probar una inferencia, permita tomar la decisión de aprobar o rechazar la hipótesis, sabiendo que está basada en un n muestral suficiente para ello.
Es correcto mencionar que existen variados métodos para el cálculo de tamaño muestral, según el diseño de estudio estos son:
- -
Estudios de correlación
- -
Estudios de pruebas diagnósticas
- -
Estudios de no inferioridad
- -
Estudios caso control, para obtener magnitud de OR específicas, entre otros.
Solo se han explicado los más frecuentemente utilizados en investigación clínica14.
III. DEFINICIÓN DE LAS VARIABLES: TIPO VARIABLES, LA ESCALA DE MEDICIÓN Y LA UNIDAD DE MEDIDAParte de la planificación metodológica de un proyecto de investigación es definir las variables independientes o predictivas, la variable dependiente o outcome y las co-variables. Durante la planificación estadística también se deben definir las variables, respecto al tipo, su unidad de medida y cómo se describirá según el tipo de medición que tiene la variable.
Según la escala de medición existen diferentes tipos de variables:
Las que miden una cualidad (nominal o categóricas y las ordinal), se llaman cualitativas.
Las que miden cantidad, se llaman cuantitativas, que pueden ser discretas o continuas5,6,11.
1. CUALITATIVAS1.1 Nominal o categóricas: Son aquellas que se clasifican en categorías, etiquetas. Dentro de estas, pueden ser dicotómicas, en que solo hay dos categorías y son auto- excluyentes. Ejemplo: vivo|muerto, enfermo|no enfermo, sexo masculino|femenino.
Policotómicas, hay más de dos categorías y no necesariamente son auto-excluyentes. Ejemplo, causas de Insuficiencia cardiaca: Hipertensión arterial, arritmia, enfermedad valvular, hipertrofia ventricular.
En las variables nominales no hay un orden establecido, no tienen un valor.
1.2 Ordinal: Tiene un sentido de orden, que está implícito, sin que sea una magnitud o cantidad. Por lo que no tienen unidad de medida. No obstante, existen instrumentos que se usan para evaluar una condición, donde el autor le asigna un número para facilitar la interpretación de éste, pero eso no significa que la cualidad sea una cantidad1,8,9. Un ejemplo de esto, son las pruebas de evaluación de funcionalidad que tienen puntaje, que son construcciones artificias, donde a una cualidad y según su nivel de cumplimiento, se le asigna un valor numérico arbitrario. Aunque tiene un número asignado, no puede tener decimales y por lo tanto, no tiene sentido cuantificar la diferencia o la razón entre los dos valores. Es por esto, que no sería matemáticamente correcto describir los puntajes con media o promedio.
Ejemplos: Niveles de gravedad: leve, moderada, severa.
Escalas o Puntajes: EVA (1-10), Glasgow (3-15), Apgar: 1-9
Un puntaje de dolor EVA: 1 a 10. Si el sujeto 1 tiene EVA=4 y el sujeto 2 tiene EVA=8
No se puede interpretar que el niño 2 tuvo el doble de dolor que el sujeto 1. Solo que el sujeto 2 tuvo al parecer más dolor que el sujeto 1. ¿Cómo se interpretaría que el promedio de dolor fue de 6.5?
2. CUANTITATIVASSon variables que son una cantidad, se refleja una magnitud, por lo que existe un orden natural en estas variables en la escala numérica. Tienen una unidad de medida.
Existen dos tipos de variables cuantitativas:
2.1 Discreta: Atributo que no puede tomar valores decimales. Son variables de conteo, tales como, días de hospitalización, n° de hijos, n° de fallas, n° de muertes. No es factible tener 1.5 hijos, se tienen 1 o 2 hijos.
2.2 Continua: Una variable continua es aquel atributo que puede asumir un número infinito de valores dentro de un determinado rango. Tienen una unidad de medida y tiene una distribución en el plano cartesiano del eje x, también llamadas intervalares.
Las variables medidas en escala de razón, el cero indica la ausencia de la variable.
Para describirlas se debe determinar si tiene distribución normal/Gaussiana (≈N) o no. Debido a su importancia para el proceso de descripción y análisis estadístico, se explicará brevemente el concepto.
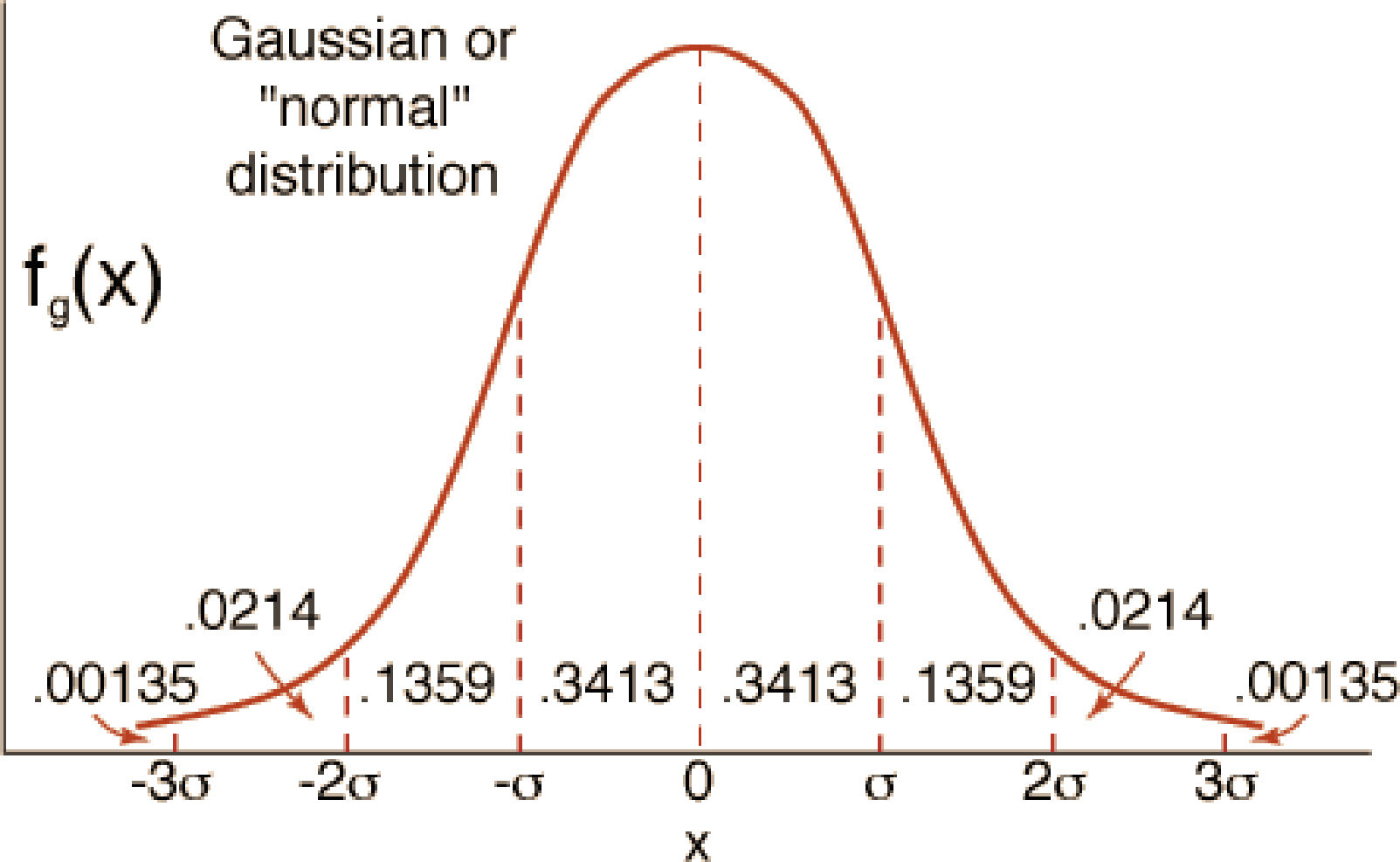
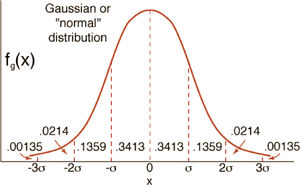
Distribución Normal, Paramétrica o Gaussiana ≈NFue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) formuló la ecuación de la curva de normalidad “la campana de Gauss”. La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas μ, σ 1,2,5,6,8,9 respectivamente.
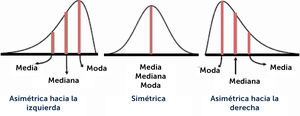
Características de la distribución normal
- •
La curva tiene un solo pico, por consiguiente, es unimodal, tiene una moda o dato más frecuente. Presenta una forma de campana.
- •
La media de una población distribuida normalmente se encuentra en el centro de su curva normal.
- •
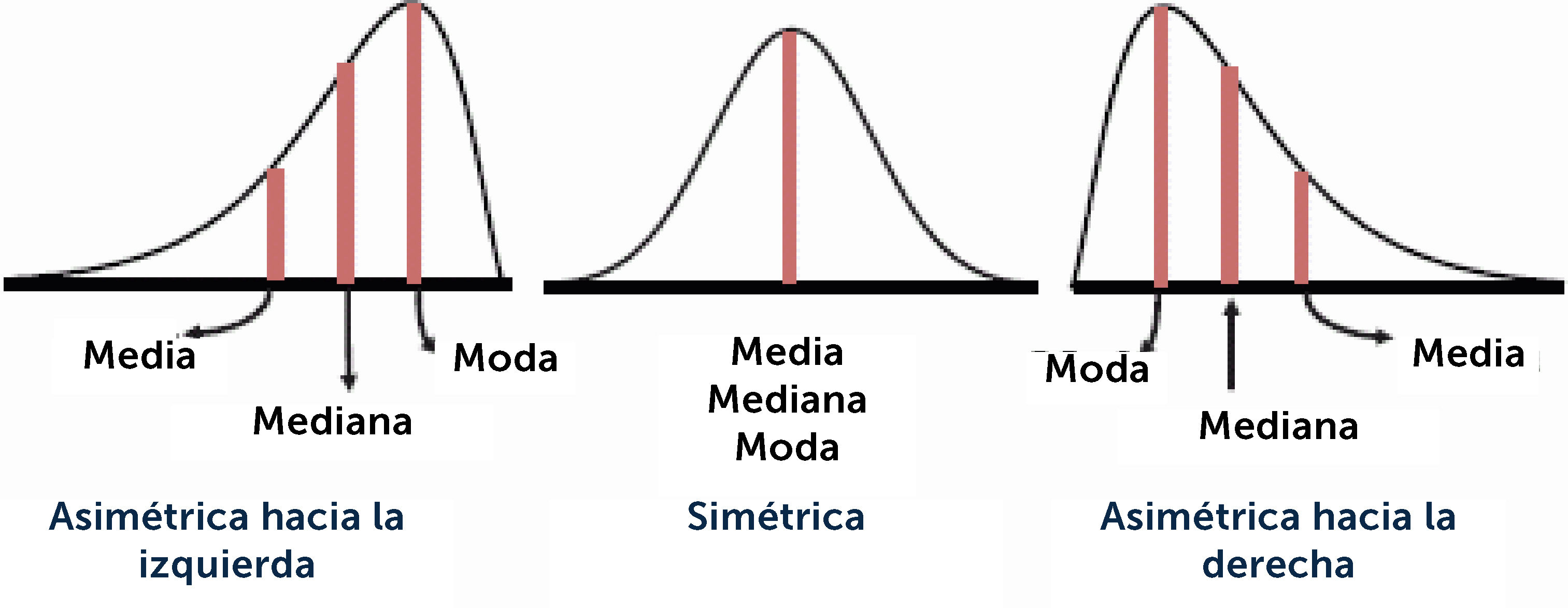
A causa de la simetría de la distribución normal de probabilidad, la media, la mediana y la moda poseen el mismo valor y se encuentran en el centro.
- •
Las dos colas (extremos) de una distribución normal de probabilidad se extienden de manera indefinida y nunca tocan el eje horizontal.
- •
A causa de la simetría de la distribución normal de probabilidad, la media, la mediana y la moda poseen el mismo valor y se encuentran en el centro. Figura 6.
Conocer la distribución de las variables continuas es relevante porque definirá los estadígrafos de tendencia central y de variabilidad que deben usarse, para que la descripción de la información sea creíble. Además, definirá las pruebas estadísticas que se podrán usar para la comparación de dos o más grupos, al igual que el tipo de regresión para medir la asociación entre la variable independiente y dependiente.
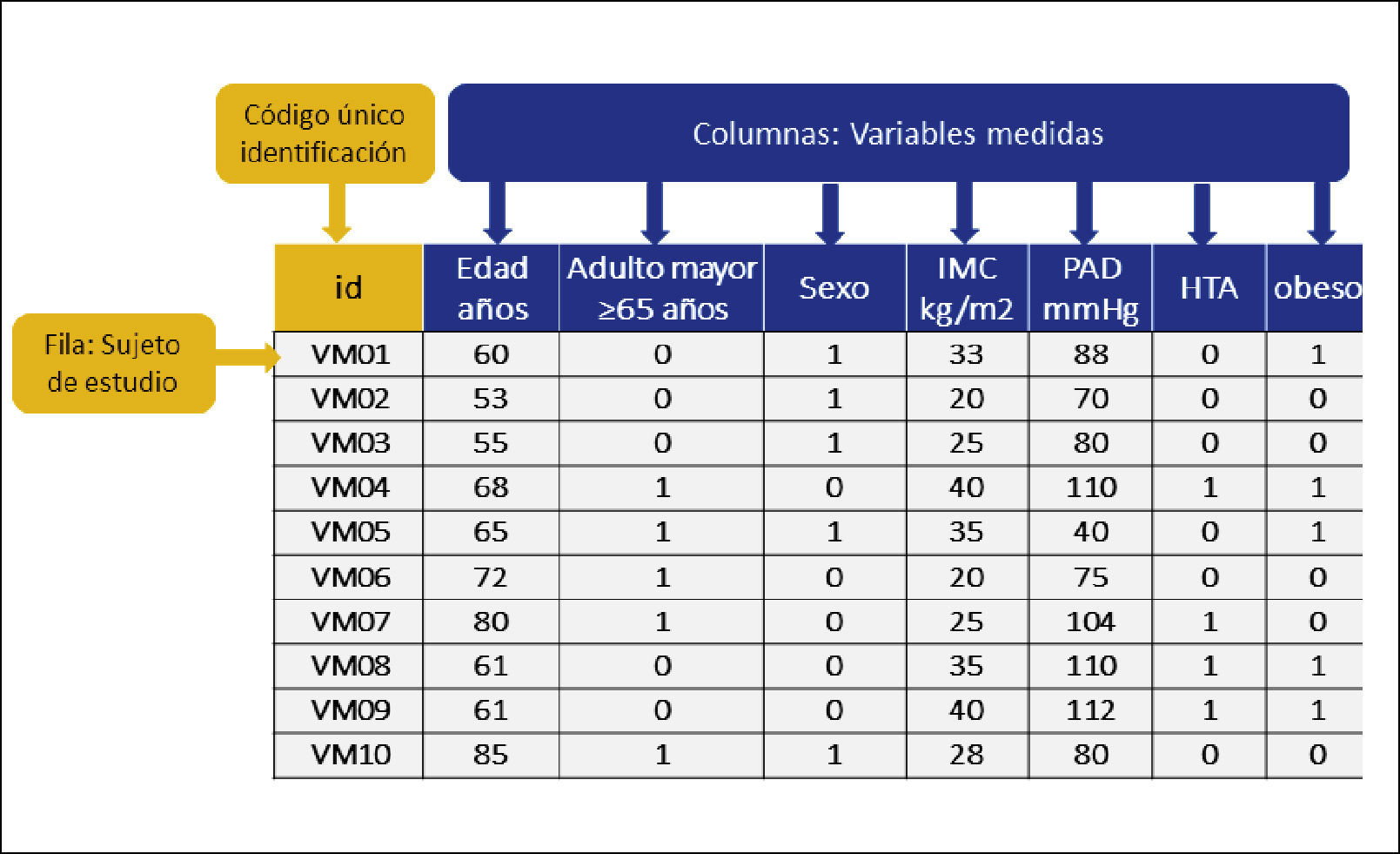
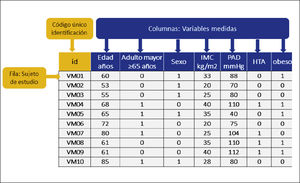
IV. PLAN DE TABULACIÓN DE LA BASE DE DATOS, DESCRIPCIÓN Y ANÁLISIS DE LA INFORMACIÓN RECOLECTADA1. PLAN DE TABULACIÓN DE LA BASE DE DATOSUna base de datos es una estructura en la cual se almacenan, con un orden definido, un grupo de descripciones sobre determinado sujetos o unidades de análisis ya medidas (variables), para finalmente ser un conjunto de datos pertenecientes a un mismo contexto y almacenados sistemáticamente para su posterior uso. La estructura está hecha de columnas y filas. Cada columna se titula con el nombre de la variable que será medida. Las filas estarán conformadas por cada unidad muestral. Figura 7.
La definición de las variables tanto en su tipo (independiente, dependiente y co-variables), como en su escala de medición, es el paso previo básico para poder construir la base de datos. Aquellas que serán dicotómicas, las que serán policotómicas o tendrán categorías o cuáles variables se registrarán en forma numérica. En las variables numérica se debe definir la unidad de medida y registrar en el título la columna. Es recomendable, registrar en escala continua todas las variables que sea posible, aunque posteriormente en el análisis se vayan a categorizar, porque si se registra como categoría, no será posible transformarla a variable continua. Por ejemplo, el hábito tabaco. Es conveniente registrar el n° de cigarrillos/día y posteriormente categorizar según el investigador estime conveniente para el análisis.
Para ello es conveniente construir un diccionario de datos con el fin definir ordenadamente cómo se tabularán las variables y se describen todos los códigos asignados a cada una. Es importante para la persona que registrará y analizará la base de datos ya codificada.
Protección de la confidencialidad de la informaciónEs importante que los investigadores tengan presente que todo dato es del sujeto de estudio y por lo tanto, es necesario solicitar su consentimiento informado para registrarlos, describirlos y analizarlos. Toda persona tiene derecho a la protección de la confidencialidad de su información y es por ello, que los análisis estadísticos deben realizarse sobre bases de datos codificadas, donde no exista información que pueda identificar al sujeto de estudio. Para esto, se construye una base de datos madre, que contiene la identificación del participante, que debe ser guardada en un lugar seguro. El análisis de la información se debe realizar en una base codificada. ¿Cómo se hace? Se asigna un código o identificador para cada sujeto (ID). El código debe ser propio del proyecto y debe ser distinto a cualquier información personal del paciente. La base de datos codificada no debe contener información que pueda ser identificable, tales como el nombre, las iniciales, fecha de nacimiento o ficha clínica del paciente.
El investigador principal debiera ser el responsable de la base de datos y aquellos que ingresen información, deben tener una clave de acceso personal e intransferible. Es necesario formar a todos los co-investigadores o colaboradores que vayan ingresar la información, respecto a las variables, cómo registrarlas, los rangos de seguridad, los datos perdidos y usar un sistema de protección de errores en el registro de los datos.
Descripción de los datos
La estadística descriptiva tiene el objetivo de describir cuantitativamente un conjunto de datos. Para ello se utilizan diferentes recursos estadísticos, tales como los estadígrafos de orden, centralización y variabilidad, que son números resúmenes de los datos recolectados, que pueden porvenir de estudios poblacionales o muestrales.
Durante la planificación del análisis estadístico se deben definir las formas de presentar la información recolectada en la muestra. A continuación se explicarán tales métodos.
Estadígrafos de orden, centralización y variabilidadLa estadística llama estadígrafos o estadísticos, a números resúmenes, que permiten extraer conclusiones a cerca de la estructura de una muestra o una colección de datos. Estos números son construidos considerando toda la información que contiene la muestra, es decir consideran todos los datos que han sido recolectados. Es por ello la relevancia de utilizar los estadígrafos correctos de acuerdo con el tipo de variable que se desea describir.
Se construyen estadígrafos para distintos fines. Los tres tipos más conocidos por su amplio uso en la estadística descriptiva son8,9,16:
- 1.
Estadígrafos de orden
- 2.
Estadígrafos de tendencia central
- 3.
Estadígrafos de variabilidad.
1. Estadígrafos de orden
- -
El máximo, X(n) y el mínimo, X(1), que aparecen en forma instantánea al ordenar la muestra.
- -
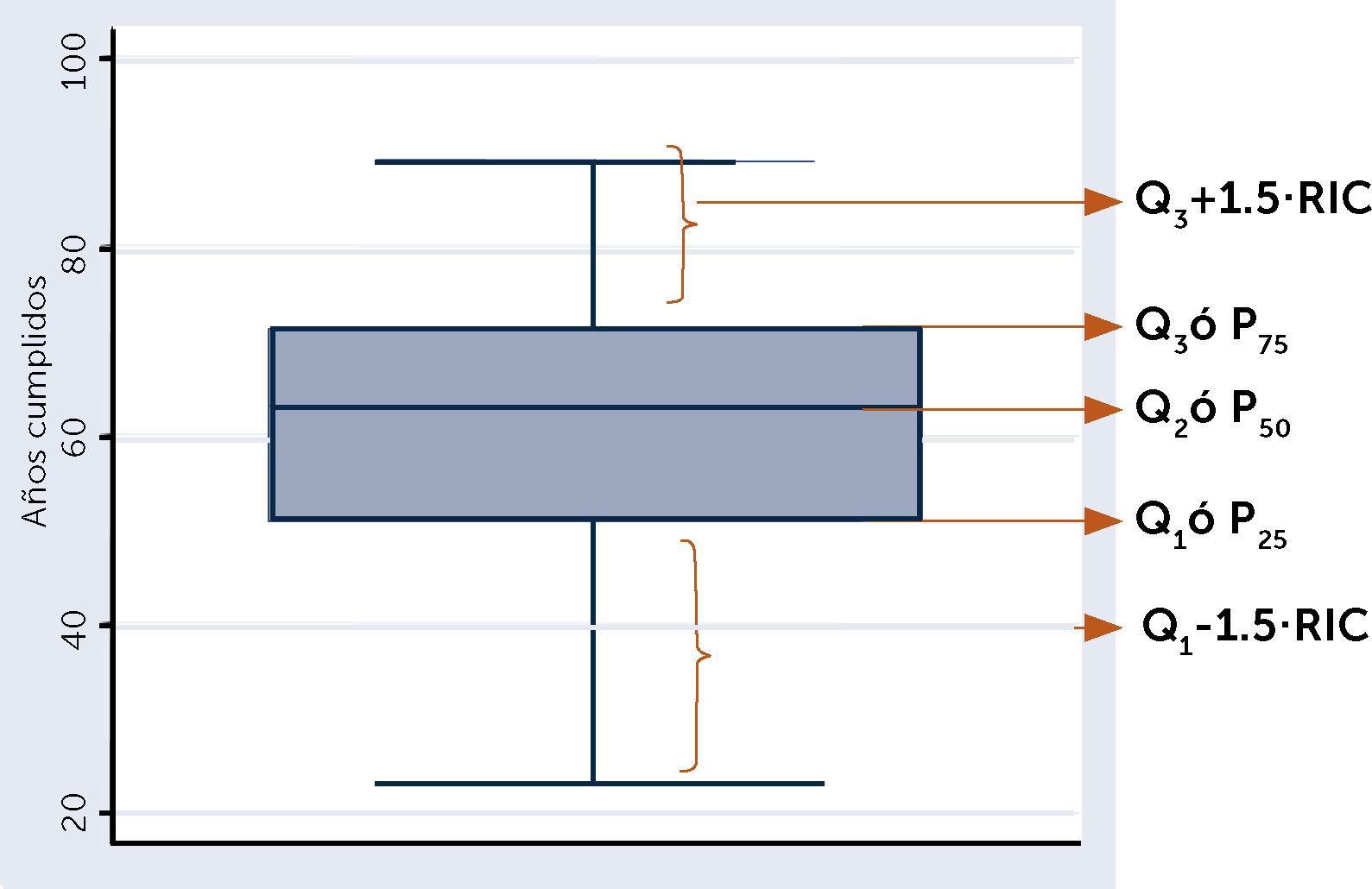
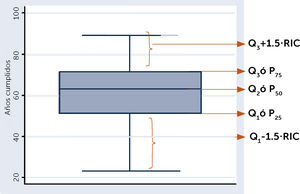
Percentiles: A cada uno de los números que dividen la muestra en 100 partes iguales, en consecuencia, ellos son 99, y se denotan por P(k), donde k es el orden del percentil indicado. Los percentiles más conocidos y usados:
Los cuartiles: son tres, denotados por Q1, Q2 y Q3, que corresponden respectivamente a los percentiles P25, P50 y P75, ellos dividen la muestra en cuatro partes iguales.
Estos percentiles son de particular interés, principalmente el percentil cincuenta (P50), recibe el nombre de mediana y divide la muestra en dos partes iguales.
En el gráfico de cajas se pueden observar los P25, P50 y P75. Ver figura 8.
Otros percentiles que se usan frecuentemente son:
Los quintiles: son cuatro, denotados por C1, C2, C3 y C4, que corresponden a los percentiles P20, P40, P60 y P80 ellos dividen la muestra en cinco partes iguales.
Los deciles: son nueve, denotados por D1, D2,...,D9, que corresponden respectivamente a los percentiles P10, P20,..., P90, ellos dividen la muestra en diez partes iguales.
2. Estadígrafos de centralización o de tendencia central
Cuando se observa un fenómeno cuantitativo, interesa saber si los datos recolectados se aglutinan en torno a ciertos valores representativos que son propios del fenómeno estudiado.
Estadígrafos de tendencia central, son:
Moda: Es el dato de mayor frecuencia de aparición. Apropiada para describir datos medidos en escala categórica o nominal, por ejemplo, sexo y variable en escala ordinal.
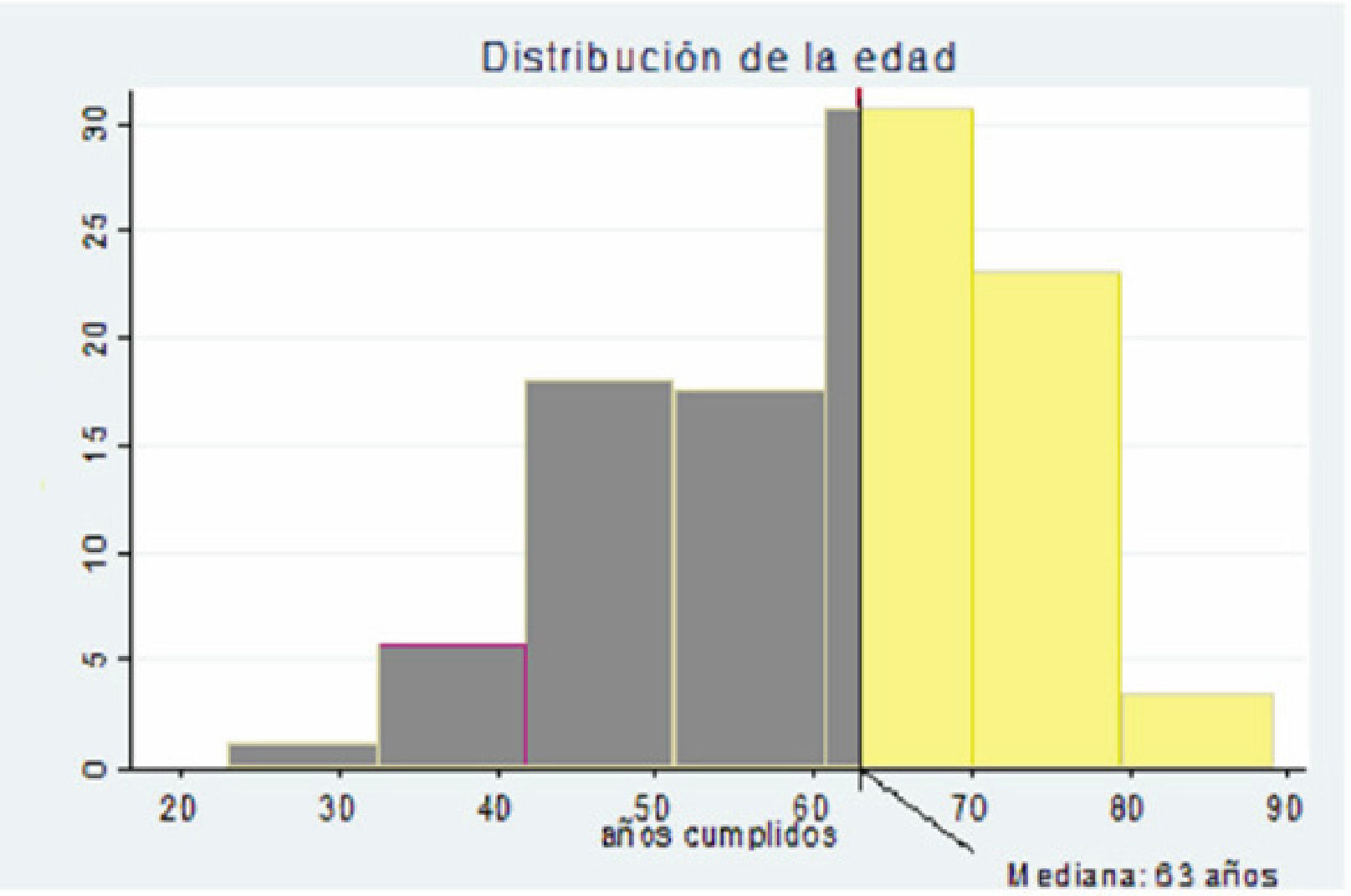
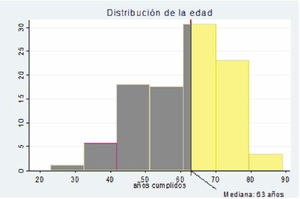
Mediana (P50): Es el punto que divide a la muestra en dos partes iguales. Es apropiada para describir datos medidos en escala:
- •
Ordinal
- •
Discreta o continua
- •
Es un estadígrafo de posición y de centralización. Figura 9.
Media o promedio
Es el punto donde se ubica el centro de masas de la muestra. Se interpreta como el valor al cual se pueden asimilar todos y cada uno de los datos. Pero la media describe bien, sólo si la muestra es homogénea y/o simétrica. Solo se puede calcular y usar para describir en variables en escala continua, con distribución normal, pero desafortunadamente es el estadígrafo central más utilizado, conocido y podría decir, abusado. Cuando una variable continuas no tiene distribución normal, la media se ve influida por los valores extremos, lo que hace que se aleje de la moda y de la mediana. En la figura 10 se observa la diferencia de la posición de la moda, mediana y media dependiendo del tipo de distribución, simétrica, asimétrica la izquierda o a la derecha. Notar que la media solo puede describir correctamente cuando ≈N.
Análisis de los datos
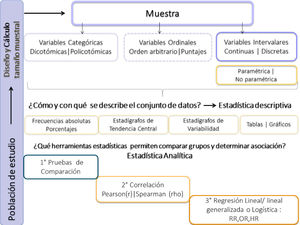
La estadística analítica tiene por objetivo comprobar hipótesis o establecer relaciones de causalidad en un determinado fenómeno. Es también llamada estadística inferencial. Es un área de la estadística que se dedica al análisis y a la elaboración de los datos con métodos basados en probabilidades, para la toma de decisiones en salud5,6. En forma práctica, cuando se habla de análisis de datos, significa la comparación de estadígrafos o porcentajes, dependiendo del tipo de escala de la variable y posteriormente si existe diferencia estadísticamente significativa entre los grupos, se procede a determinar la correlación entre las variables, para luego medir la asociación entre una o más variables independientes o predictoras (X) y la variable dependiente, también llamada efecto o outcome(Y).
Para ello el análisis estadístico se podría ordenar en tres etapas:
1° Comparación del efecto entre grupos que están y no están expuestos a la variable independiente
Para ello se utilizan pruebas estadísticas de comparación y según la distribución de las variables, serán pruebas paramétricas (si la variable distribuye normal) o no paramétricas (si la variable no distribuye normal). Según la escala de la variable que se va a comparar tendremos:
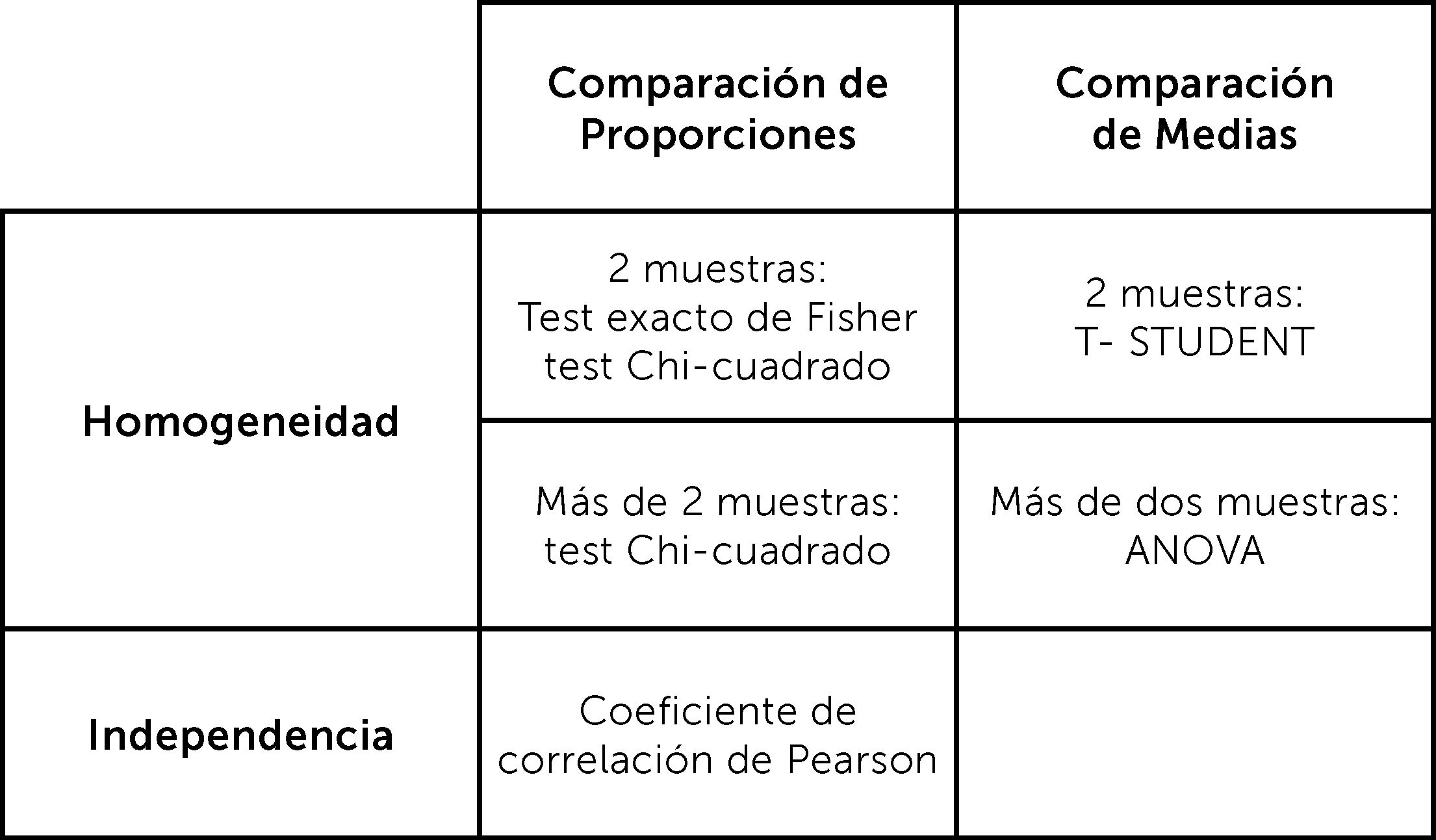
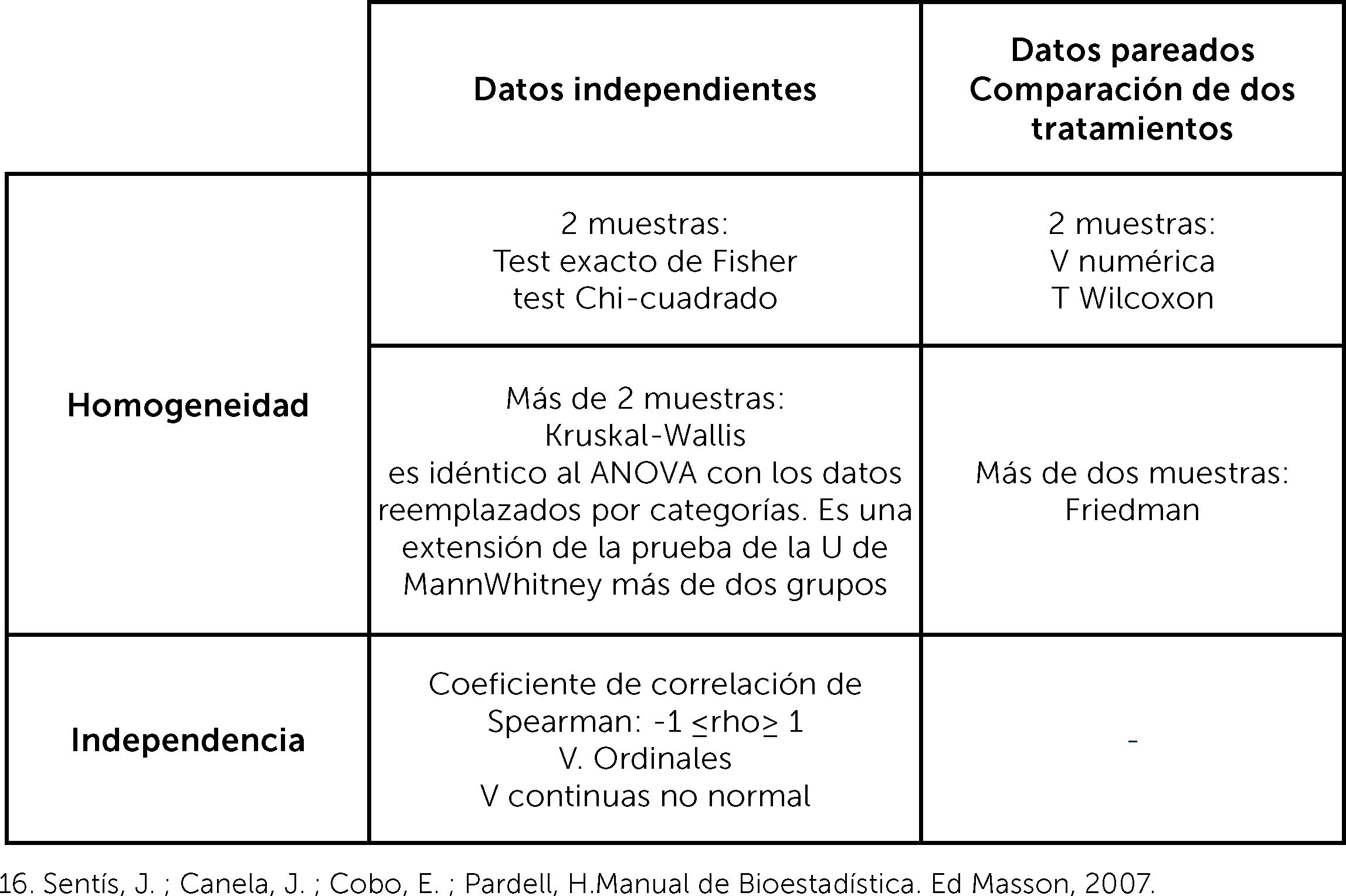
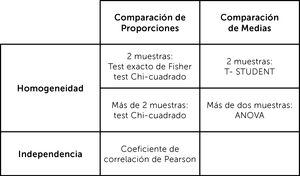
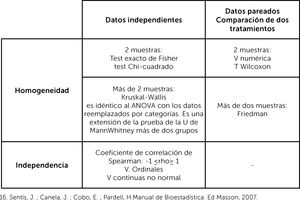
Variables categóricas: se usa la prueba exacta de Fischer, en caso de comparación de dos grupos y una muestra pequeña (≤30) o prueba de Chi2, en caso de dos grupos con muestra >30 o más de dos grupos.
Variables de escala continua: si distribuye normal, se comparan medias. Si son dos medias se usa la prueba de Tstudent y si son tres o más medias, la prueba de análisis de la varianza (ANOVA). Cuando no distribuye normal, se usa prueba de Mann Whitney comparación de dos medianas, Kurskall Wallis, comparación de tres o más medianas. Esto es cuando se comparan grupos independientes. Cuando se comparan grupos que no son independientes, es decir pareados es necesario usar otras pruebas. ¿Qué significa grupos pareados? Esto es cuando el resultado del segundo grupo depende del resultado del primer grupo, es decir, cuando se compara a una misma muestra en dos tiempos distintos. Porque los resultados que se obtengan en el segundo tiempo de medición son dependientes de los resultados del primer tiempo de medición.
En ese caso, si se comparan dos medias, se usa la prueba de Tstudent para grupos pareados. Si son dos medianas, se usa la prueba de Wilcoxon para grupos pareados, si son tres o más medianas prueba de Friedman1,2,8,9,16.
2° La determinación de la correlación entre la variable independiente y el efecto, con el coeficiente de correlación
La correlación es el grado de variación conjunta de dos variables numéricas o continuas. Se determina con un coeficiente de correlación, que será de Pearson (r), en el caso que la variable distribuya normal, o de Spearman (rho) en el caso que no distribuya normal. Los valores del coeficiente irán desde 1, correlación positiva perfecta, mientras una variable aumenta, la segunda variable también es lineal y en una razón de 1:1. Hasta -1, correlación negativa perfecta, mientras una variable aumenta su valor, la segunda variable disminuye su valor, es lineal y en una razón de 1:1. Una correlación 0, significa que no hay correlación lineal, pero no implica que pueda haber otro tipo de correlación, tales como cuadrática, cúbica, entre otras1-6.
Existen múltiples pruebas de comparación de grupos y de correlación, para ser usadas en variables con distribución normal o paramétricas, como para aquellas que no tienen distribución normal, o no paramétricas.
El objetivo de este artículo no es profundizar en la estadística analítica, pero sí que se familiaricen con los nombres de los test más frecuentemente usados en los estudios de investigación clínica. El desarrollo de una discusión sobre las metodologías estándares respecto a las más actuales, va más allá del humilde objetivo del artículo. Ver figuras 11 y 12, donde se muestra un resumen de las pruebas paramétricas y no paramétricas3° La determinación de la asociación entre la variable independiente y el efecto, con la regresión
Para determinar el grado de asociación entre una variable independiente y una dependiente, se usa la regresión. Su forma más sencilla, es la regresión lineal simple, que es una técnica estadística que analiza la relación entre dos variables cuantitativas que distribuyen normal y donde se trata de verificar que existe una relación lineal. Una asociación lineal, significa que a medida que la variable independiente está presente, también está presenta en la misma proporción la variable dependiente17-20.
La regresión supone que hay una variable fija, que está controlada por el investigador (variable independiente) o predictora (que predice el efecto), también considerada como de exposición o posible “causa”. Y otra que no está controlada, que es la variable respuesta, o efecto o dependiente. Supone que es la respuesta al estar expuesto a la variable independiente. La variable respuesta siempre ocupa el eje de ordenadas “Y” y la variable independiente el eje las abscisas “X”.
Cuando se quiere relacionar una variable “X” con una variable dependiente Y, es una regresión simple o univariada. Si se quiere relacionar dos o más variables independientes a una variable dependiente, se le llama regresión bivariada, o multivariada respectivamente.
Los tipos de regresión dependen del tipo de escala de la variable dependiente o respuesta. Si es continua, será regresión lineal (si la respuesta distribuye paramétrica) o regresión lineal generalizada (si la respuesta distribuye no paramétrica).
El modelo de regresión reporta los coeficientes βeta.
Cuando la respuesta está medida en escala dicotómica, tiene distribución binomial (1 o 0), se usa la regresión logística. Es este caso, el modelo reporta la medida de asociación Odds Ratio (OR)4,5
¿Cómo se evalúa si el modelo de regresión tiene una buena capacidad de predecir la variable dependiente o la variable respuesta? Se hace a través del coeficiente de determinación (R2). Este es la proporción de la variación total de la respuesta Y que es explicada por la variación de X. El R2 indica que tan bien se ajusta el modelo a los datos observados.
Para visualizar mejor el grado de relación entre la variable respuesta y cada variable independiente, el gráfico de dispersión es un adecuado recurso.
Medidas de AsociaciónSon aquellas medidas que reporta la magnitud de asociación entre la variable explicadora X y la variable dependiente Y. Te dice la fuerza con que se asocian ambas variables.
Las medidas, más frecuentemente utilizadas en los estudios, el
- -
Riesgo relativo RR. Se puede estimar solo en los estudios prospectivos. Esto es porque mide el riesgo, que solo se puede calcular en los estudios prospectivos.
- -
Odds ratio: solo se calcula en estudios con respuesta dicotómica, sale de una regresión logística.
Dado que el objetivo del artículo es presentar conceptos básicos de la bioestadística aplicada en investigación, no se va a profundizar en la estadística analítica, porque va más allá del alcance de éste.
- -
Hazard ratio (HR). Se puede calcular en estudios prospectivos y es el resultado de la regresión de riesgos proporcionales de Cox.
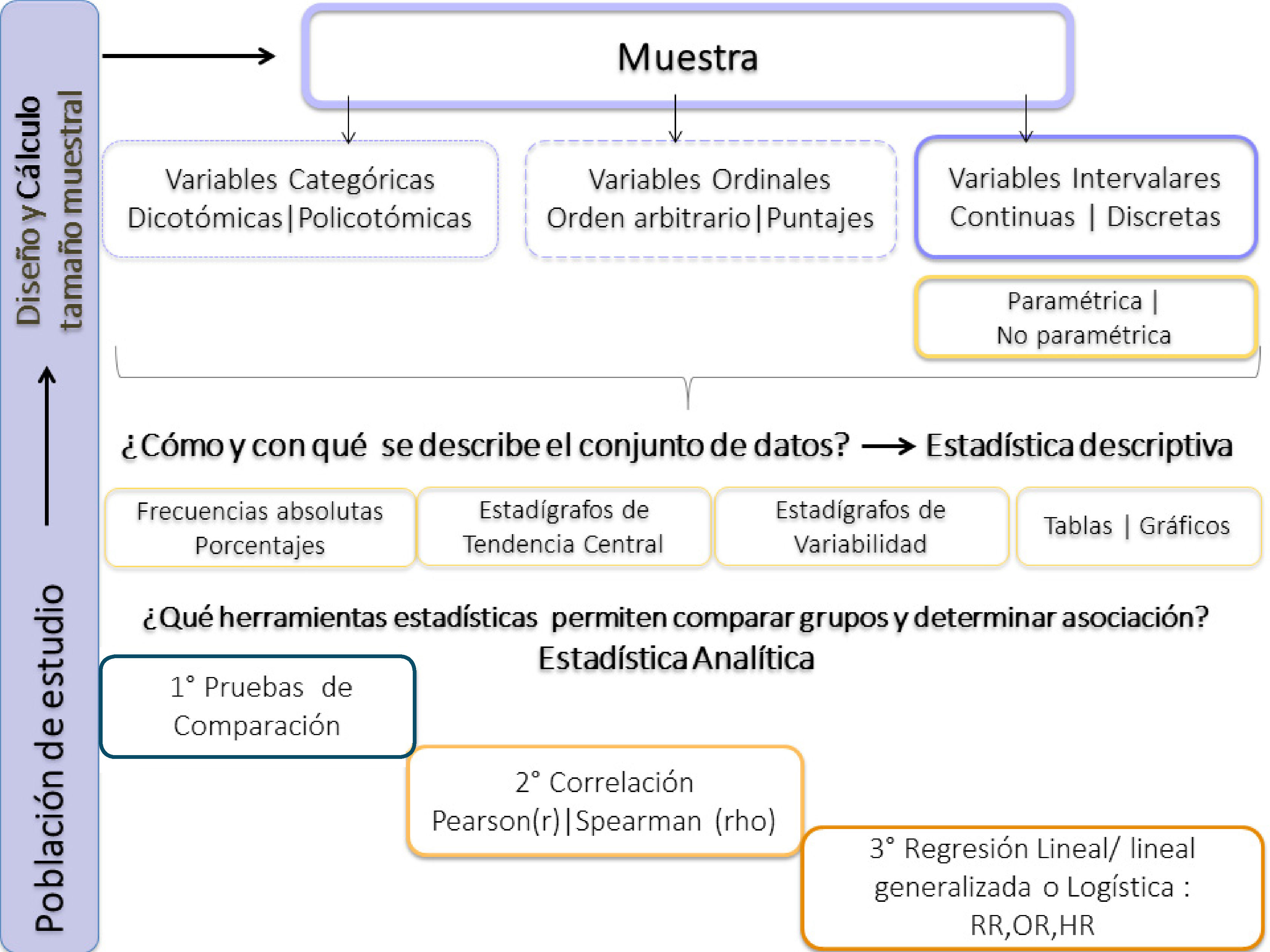
A continuación, se presenta un diagrama que resume las funciones de la bioestadística en un estudio de investigación. Figura 13.
SÍNTESISLa estadística es una herramienta que no es posible soslayar en la investigación científica, porque es lo que permite probar matemáticamente una hipótesis y extraer conclusiones válidas. La estadística está a disposición de los investigadores y existe variada literatura y métodos para aprender y acercar esta disciplina al investigador clínico. Solo hay que mirarla de forma amigable, aceptando la importancia y utilidad que tiene. No olvidar que ésta debe ser el instrumento que permita cumplir con los objetivos del estudio y responder la pregunta de investigación. Es fundamental que todo el proceso estadístico, sea metodológicamente adecuado, porque los resultados dependerán la validez interna del estudio y eso es, una rigurosa prevención y control de sesgos de información, selección y confusión. Si la validez interna es deficiente, con alto nivel de sesgo (errores sistemáticos), independiente que la estadística sea la correcta, los resultados serán espurios, porque la medición fue la que incurrió en el error. No hay que olvidar que los resultados del estudio dependen de la medición (observación) y los errores sistemáticos en ésta, llevan a sesgo de información y confusión. Por lo tanto, hay que prevenir el error en quién mide (observador), el error con qué se mide (instrumento) y el error a quién se mide (observado).
Finalmente, considerar que las conclusiones estadísticas son probabilidades, porque la medicina no es exacta y es solo una parte de la verdad. A ésta debe sumarse el criterio y la experiencia clínica del profesional de salud y la necesidad del paciente, siendo estos los elementos que completan el escenario para la toma de decisiones en beneficio de los pacientes.
Declaración Conflicto de InterésComo autora declaro libremente no haber recibido fondos, ni otros beneficios para la publicación de este artículo.