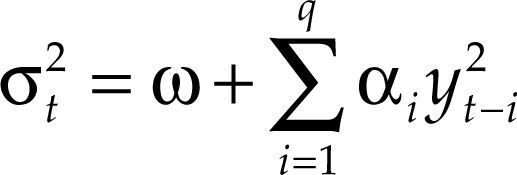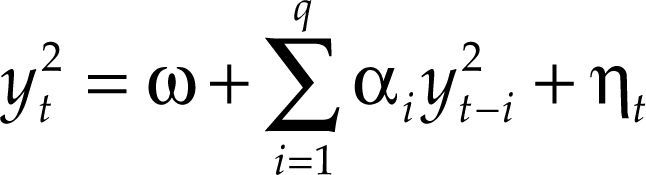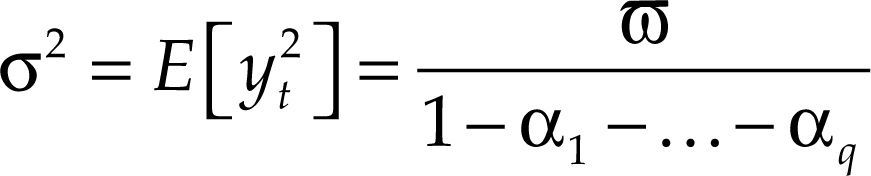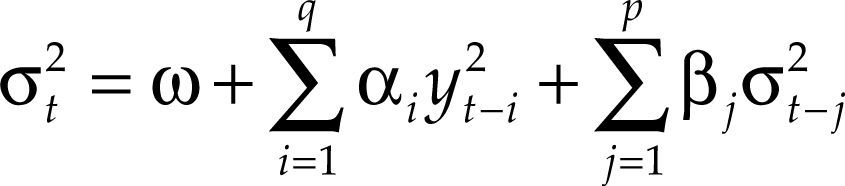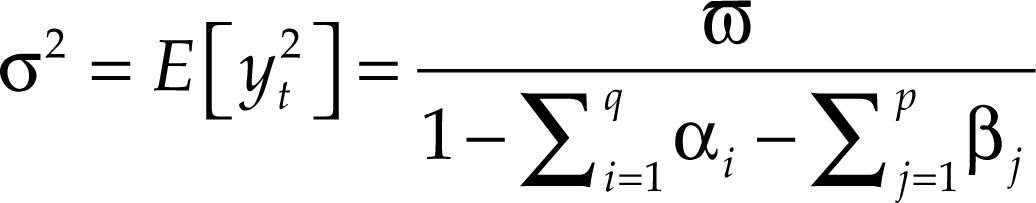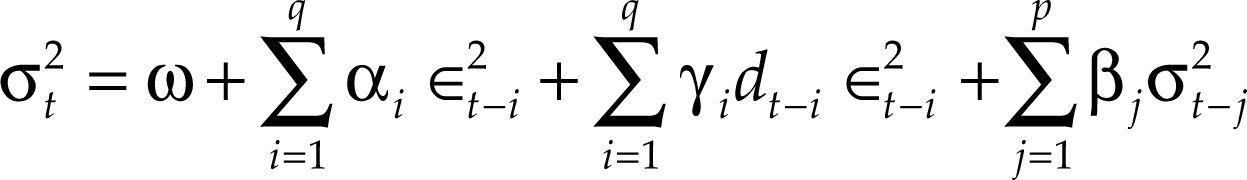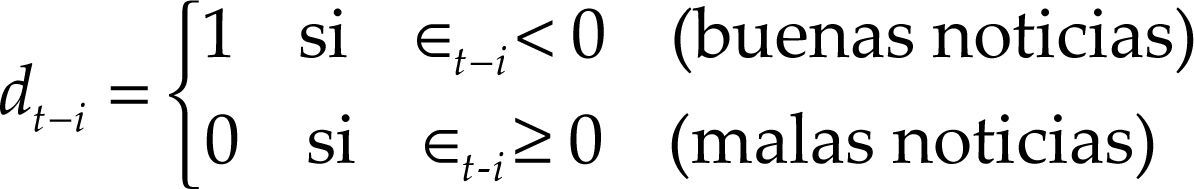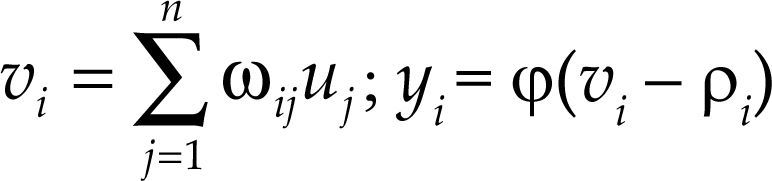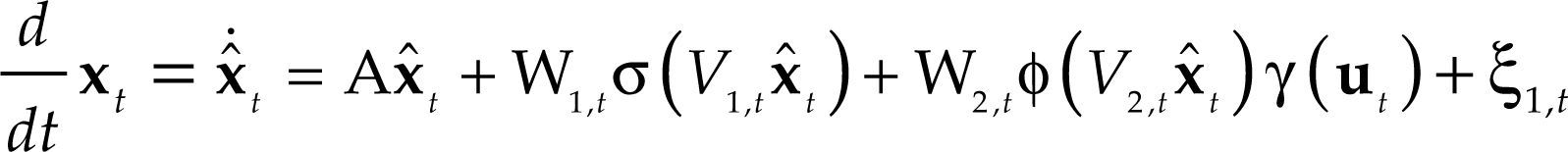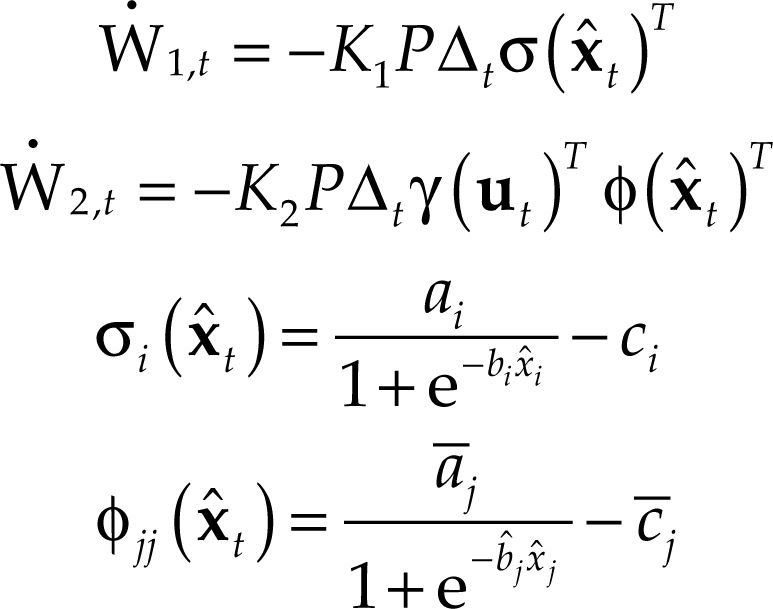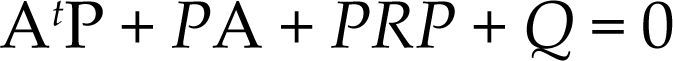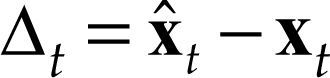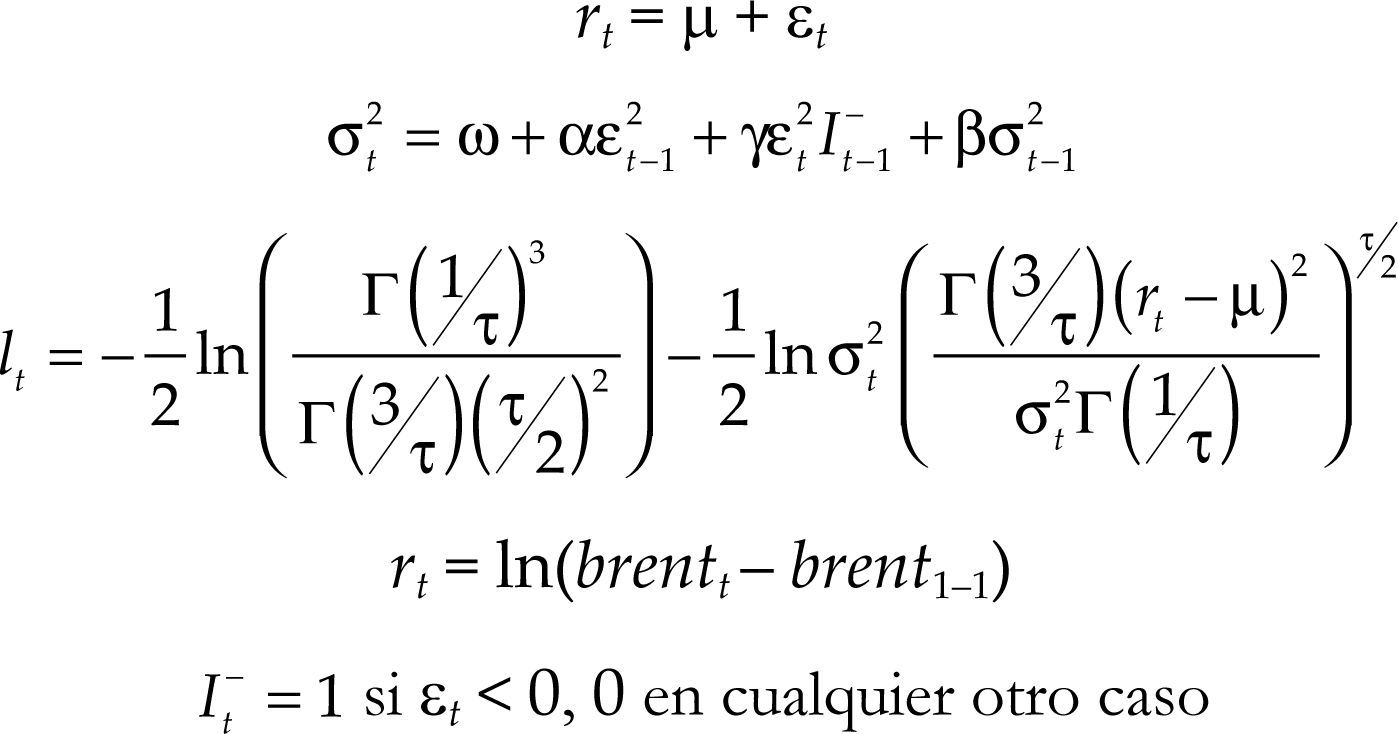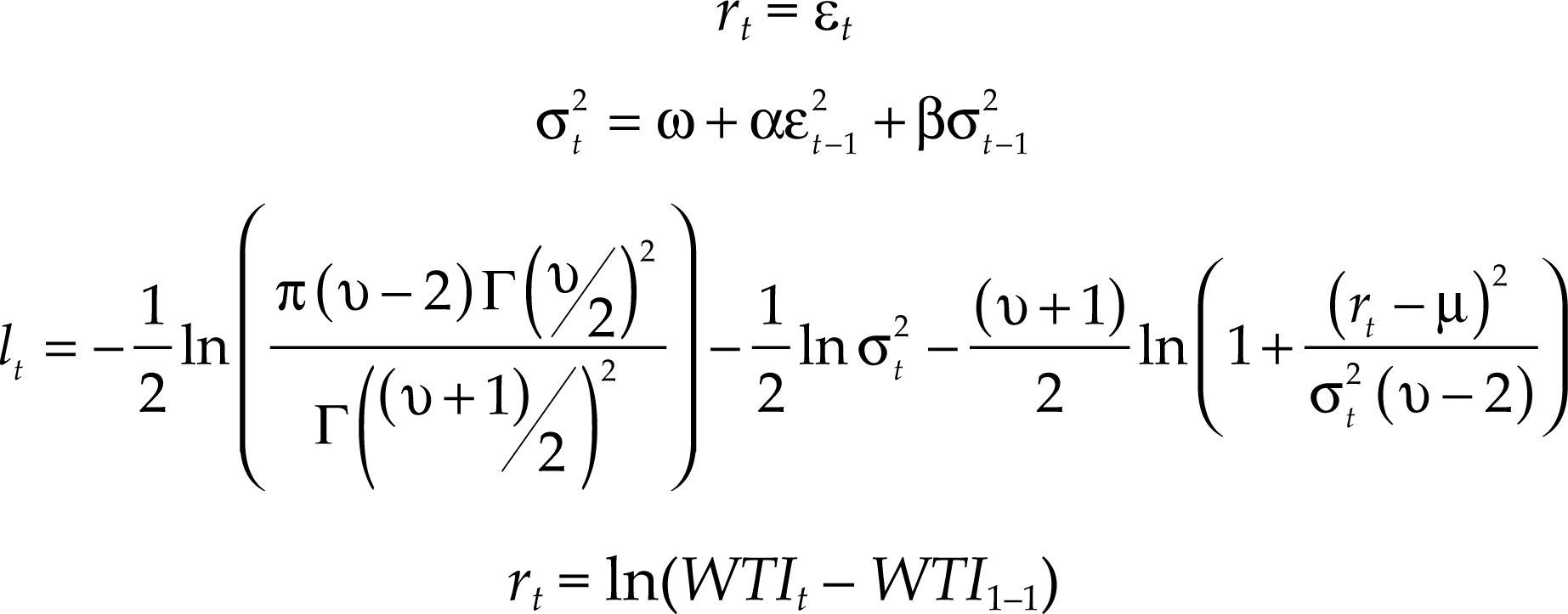El objetivo del presente trabajo es mostrar las ventajas que tiene el utilizar a las redes neuronales diferenciales (rnd) como un método alternativo eficiente en el cálculo de pronósticos de precios futuros de activos financieros, para lo cual se hace un comparativo con modelos de la familia garch, al llevar a cabo el pronóstico de precios de cierre de barriles de petróleo crudo de los tipos West Texas International (wti) y Brent. Los resultados demuestran que el uso de las rnd tiene, en esencia, la misma precisión que los valores obtenidos con el modelo tgarch(1,1) y son superiores a los obtenidos mediante el modelo garch(1,1), al calcular los pronósticos de precios de los barriles de petróleo Brent y wti respectivamente durante el periodo de descripción, del 2 de enero de 2013 al 24 de febrero de 2015, y del periodo de pronóstico, del 25 de febrero al 10 de marzo de 2015. Sin embargo, el esfuerzo realizado para obtener tales resultados con la familia de modelos garch es significativamente mayor que cuando se utilizan las rnd, esto apoya la propuesta de utilizar las rnd como un método alternativo fiable en el análisis de series de tiempo.
The aim of this paper is to show the advantages of the use of neural networks differentials (rnd) as an efficient alternative method in calculating the forecasts of future prices of financial assets, for which a comparison is made with models of the garch family, to carry out the forecast of future closing price of crude oil barrels, types West Texas International and Brent. The results shows that the use of rnd has essentially the same accuracy as the values obtained with the tgarch (1,1) model and are superior to those obtained by the garch (1,1) model to calculate price forecasts barrels of crudes Brent and wti respectively during the period of description, from January 2, 2013 to February 24, 2015 and the forecast period from February 25 to March 10, 2015. However, the effort made to obtain such results with the family of garch models is significantly higher than when using the rnd, this supports the proposal to use the rnd as a reliable alternative method in the analysis of time series.
Desde la aparición de los trabajos seminales de Engle (1982) y Bollerslev (1986) en los que presentaron el modelo autorregresivo condicional heterocedástico (arch) y el arch generalizado (garch) respectivamente, el análisis de las series de tiempo de fenómenos económicos y financieros, cuyo comportamiento en general es no lineal, ha sido dominado por estos modelos; la razón fundamental es que gracias a que incorporan las relaciones funcionales que permiten relacionar la volatilidad condicional actual con las volatilidades condicionales pasadas, así como las innovaciones, es posible incluir las variaciones temporales de la volatilidad en los valores de la serie de tiempo analizada. Esto permite tener una modelación estadística más robusta de las series temporales de origen financiero o económico, práctica que ciertamente ha dado muy buenos resultados en los procesos de seguimiento o descripción de la serie y, más importante aún, el poder elaborar un pronóstico de los valores futuros de la serie en un intervalo de tiempo.
Por otro lado, existe una técnica que tiene sus orígenes en el estudio de la inteligencia artificial, la cual data de un trabajo de McCulloch y Pitts (1943), en el cual crearon las redes neuronales artificiales. En dicho documento, el objetivo de McCulloch y Pitts fue el de crear modelos computacionales que tuvieran la capacidad de emular el funcionamiento del cerebro humano, para lo cual utilizaron como elementos base procesos matemáticos a los que denominaron neuronas, las cuales funcionaron como nodos constituyentes de un arreglo en forma de red. El gran logro en este modelo consistió en que pudieron incorporar en ciertos nodos, los estados de otros nodos de la red de acuerdo a la estructura de ésta y a cierto orden de interacciones dentro de ella en un intervalo de tiempo, funcionando como un sistema que va censando periódicamente la información nueva, la clasifica y la incorpora al sistema, acorde con un intervalo de tiempo estipulado en el sistema. Esta característica de operación les permite adaptarse a las circunstancias cambiantes del medio donde interactúan, de aquí su gran valor que, como se puede apreciar, es en esencia el funcionamiento de una neurona del cerebro humano, de ahí el nombre de red neuronal artificial (rna). La primera red neuronal artificial fue diseñada por McCulloch y Pitts (1943), la cual era una estructura matemática que trataba de emular de manera muy simplificada el funcionamiento de las neuronas del cerebro humano, dichas estructuras se constituyeron como sistemas con n entradas y sólo una salida de información, así como con sólo dos estados posibles: activa o inactiva.
En la actualidad se utilizan rna mucho más complejas, en la mayoría de los casos de tipo discreta con una o varias capas ocultas, para las cuales se requiere un periodo de entrenamiento de la red bastante largo, normalmente más de 500 valores; y posteriormente un periodo de seguimiento o descripción de los valores de la serie de tiempo para, finalmente, llevar a cabo un pronóstico de valores futuros relativamente corto. Sin embargo, desde mediados de la década de los noventa se ha venido desarrollando un tipo de redes neuronales artificiales continuas en el tiempo o también conocidas como redes neuronales diferenciales o dinámicas (rnd), las cuales tienen entre algunas de sus ventajas sobre las rna discretas el hecho de que requieren mucho menos valores para el proceso de entrenamiento y calibración de la red, además de su mayor rapidez de acoplamiento a los cambios bruscos de los valores que tome la serie de tiempo analizada debido a que basa su convergencia en los criterios de estabilidad de Lyapunov (Poznyak, Sanchez y Yu, 2001, pp. 31-37). Estas características de las rnd les confieren un gran potencial para poder describir de manera más precisa los valores que siguen las series de tiempo económicas y financieras, cuyo comportamiento es no lineal. Esta es la herramienta que se utilizará en el presente trabajo para llevar a cabo el pronóstico de precios de cierre de barriles de petróleo de los tipos West Texas International (wti) y Brent y compararlo con los valores obtenidos al usar modelos de la familia garch.
Los resultados alcanzados por ambas clases de modelos muestran que la precisión de los pronósticos derivados con ambas metodologías es equivalente; no obstante, el esfuerzo realizado para llegar a los pronósticos mediante rnd es mucho menor que el empleado con los modelos de la familia garch, de hecho uno de los elementos más complicados usando los modelos garch fue el llevar a cabo distintas pruebas para determinar cuál modelo de esta familia describía mejor las series. Así, se llegó a la conclusión de que para la serie wti se usaría un modelo garch(1,1) y para la serie Brent lo más conveniente era emplear un modelo tgarch(1,1) (Threshold garch). En cambio, para los pronósticos con rnd se usó el mismo modelo, aplicado directamente a los valores de las series sin hacer mayores cambios. El presente trabajo está organizado de la siguiente forma: en la segunda sección se plantea una breve descripción de los modelos garch y tgarch con el fin de familiarizarse con ellos. Posteriormente, en la tercera sección, se presenta una breve introducción a las rna y, con mayor detalle, a las redes neuronales diferenciales. En la cuarta sección se exponen los resultados de aplicar ambas metodologías para pronosticar los precios de barriles de petróleo wti y Brent, mostrando en su parte final un cuadro comparativo de los resultados obtenidos. Finalmente, se presentan las conclusiones del trabajo, así como las referencias bibliográficas.
MODELOS GARCH Y TGARCHComo se mencionó antes, en la mayoría de series de tiempo de origen financiero y económico se presenta el caso de comportamientos no lineales que tienen su origen en la volatilidad de los valores de la serie. Este tipo de series muestran curtosis excesivas, volatilidades cambiantes, e incluso clusters de volatilidad, entre otras características; por ello, el estudio de la volatilidad en las series financieras se ha convertido desde hace tres décadas en un campo muy estudiado de la economía y las finanzas, prueba de ello son los trabajos de Engle (1982), Bollerslev (1986), Braun, Nelson y Sunier (1995) y Chan, Leung y Wang (2004). Aunado a la volatilidad en los fenómenos económicos y financieros, es frecuente la intervención de ciertas expectativas sobre el valor que tomen las variables en el tiempo a partir de situaciones previas, ya sea de periodos de baja volatilidad con cambios suaves o periodos de cambios bruscos en los valores de las variables analizadas, situación que genera valores esperados condicionados por la varianza del periodo previo. Este comportamiento fue considerado por Engle (1982) al proponer un modelo que incluía una varianza condicional no constante expresada como una función lineal del cuadrado de los valores pasados considerados en el modelo. Este es el llamado modelo arch, el cual —desde su aparición— ha sido de gran ayuda para poder elaborar pronósticos de series de tiempo económicas y financieras; sin embargo, se ha encontrado que su capacidad de predicción varía dependiendo del periodo que se considere, lo cual se debe, según McNees (1979), a que en los periodos de varianzas grandes los datos presentan un cierto grado de correlación, lo cual altera la capacidad de pronosticar de este modelo.
El modelo arch está definido del siguiente modo:
Sea ∈t una sucesión de variables aleatorias independientes e idénticamente distribuidas (i.i.d.) siguiendo una distribución normal estándar N(0,1), entonces el proceso yt será un proceso arch(q) si:
donde:con ω > 0, αi ≥ 0, i = 1,…,q.De la ecuación [1] se tiene que la varianza condicional está determinada por los valores previos yt−i2, de tal manera que es posible calcular yt2 como:
para alguna variable aleatoria ηt.Y para la varianza no condicionada se tiene la siguiente expresión:
Debido a que frecuentemente se requerían modelos arch(q) de orden elevado para poder describir la dinámica de la volatilidad condicional de una serie, Peters (2001) presentó en 1986 (Bollerslev, 1986) un modelo generalizado arch al que se le designó como garch. Este modelo contempla no sólo las variaciones de los valores de la serie, sino que también incluye los valores de la varianza condicional rezagada, de este modo es posible suavizar el efecto de las volatilidades pasadas sobre la volatilidad actual. El modelo garch está definido de la siguiente manera:
Sea ∈t una sucesión de variables aleatorias i.i.d. siguiendo una distribución normal estándar N(0,1), entonces el proceso yt será un proceso garch(p,q) si:
donde:con ω > 0, αi ≥ 0, i = 1,…,q, βj ≥ 0, j = 1,…,p.Nótese que si en la ecuación [2] se toma βj = 0, j = 1,…,p, se obtiene el modelo arch(q). Cuando en un proceso garch(p,q) se cumple la condición ∑i=1qαi+∑j=1pβj<1, entonces dicho proceso es estacionario y es posible calcular la varianza no estacionaria mediante la expresión:
Un punto muy importante a considerar es que tanto en los modelos arch(q) como en los garch(p,q) los coeficientes deben restringirse a aquellos casos que garanticen obtener varianzas condicionales positivas.
Otra característica que se presenta en las series financieras es el llamado apalancamiento (Enders, 2004), el cual consiste en un efecto asimétrico de las noticias incorporadas al modelo. Sobre la volatilidad condicional, se ha observado que las malas noticias tienen en general un impacto mayor sobre ésta que las buenas noticias. Este comportamiento no puede ser descrito por un modelo garch(p,q) puesto que, como se puede apreciar en la ecuación [3], la varianza condicional depende de los cuadrados de las innovaciones y de las varianzas pasadas, lo cual provoca que el signo de las innovaciones no modifique la volatilidad condicional presente, por lo tanto se tiene simetría en los efectos de las nuevas noticias independiente de su naturaleza. Por esta razón, Zakoian (1994) creo una modificación del modelo garch(p,q), a la cual se le denominó modelo garch por umbrales, el tgarch.
El modelo tgarch fue creado por Zakoian con objeto de poder modelar los efectos asimétricos de la incorporación de las innovaciones negativas al sistema y así modelar el efecto de apalancamiento, esto permite describir diferentes reacciones de la volatilidad condicional respecto a los signos diferentes en los rezagos de los errores, los cuales generan asimetrías en la volatilidad condicional (Zakoian, 1994). Cabe mencionar que existen dos formas de describir al modelo tgarch: la descripción original de Zakoian y la de Glosten, Jagannathan y Runkle (1993), conocida como gjr.
En este trabajo usaremos la descripción del modelo tgarch(p,q) de gjr, la cual puede expresarse de la siguiente manera (López Herrera, 2004):
donde dt–i es una variable dummy que opera como función indicadora y establece un umbral con valor de cero para clasificar a los impactos pasados:Por otro lado, el parámetro γi registra la asimetría o efecto apalancamiento que se genera con los valores negativos de ∈t–i. Cuando γi = 0, ∀i, se obtiene el modelo garch(p,q).
En la descripción del modelo tgarch(p,q) de Zakoian se modela la volatilidad condicional en vez de la varianza condicional, que es como se presenta en este trabajo en la ecuación [5], correspondiente a la versión gjr del modelo tgarch(p,q).
REDES NEURONALES DIFERENCIALESAntes de proceder a usar las redes neuronales diferenciales, rnd, se presenta una breve descripción de las redes neuronales artificiales, rna, de manera general, para después dar un mayor énfasis a la descripción de las rnd.
Redes neuronales artificialesExisten diversas definiciones del término red neuronal artificial, una de las más aceptados es la de Kohonen (1989), en la cual establece que una red neuronal artificial está constituida por un conjunto de elementos de cálculo simples, generalmente adaptativos, que están interconectados en una estructura en paralelo, obedeciendo una organización jerárquica a la cual se le llama capa, la cual le permite interactuar con algún sistema de la misma forma en que lo hace un sistema nervioso biológico.
Las rna han venido ganando mucho terreno como herramienta de modelación y pronóstico de sistemas dinámicos no lineales desde su invención en 1943, sobre todo en campos de la ingeniería, biología y aplicaciones militares, sin embargo, ya desde mediados de la década de los noventa se han venido aplicando también para modelar fenómenos económicos y financieros (Haykin, 1998; McNelis, 2005), entre sus aplicaciones se cuentan: el cálculo de precios futuros de productos derivados (Hutchinson, Lo y Poggio 1994); el pronóstico de índices de precios y cotizaciones en mercados accionarios (Hanias, Curtis y Thalassinos, 2007; Cabrera y Ortiz, 2012), y pronósticos de paridades cambiarias (Dhamija y Bhalla, 2016; Ortiz-Arango, Cabrera-Llanos y Venegas-Martínez, 2016). Algunos de los factores más determinantes en la propagación del uso de las rna como herramienta en la elaboración de pronósticos de series de tiempo financieras son: el incremento sustancial de poder de cálculo en los últimos años y su relativamente fácil implementación, pues las rna llegan a obtener resultados a partir de datos de entrada directos de la serie de tiempo sin necesidad de hacer análisis previos sobre ésta y con ellos lograr identificar patrones de comportamiento que serían muy difíciles, e incluso imposibles, de obtener con otras técnicas. Como ejemplo de un análisis comparativo entre la precisión de efectuar pronósticos de paridades cambiarias mediante un modelo garch(1,1) y un modelo basado en rna se tiene el trabajo de Charef y Ayachi (2016), en el cual muestran que la precisión en el cálculo de los pronósticos de paridades cambiarias es mayor con el modelo de redes neuronales, además de más rápido.
De acuerdo a Poznyak, Sanchez y Yu (2001, pp. 11-13), “una red neuronal artificial (rna) es un procesador distribuido masivamente en paralelo, la cual está inspirada en las redes neuronales biológicas y puede, además, almacenar conocimiento experimental y hacerlo disponible para su uso”. El conocimiento de la red se adquiere por medio de un proceso repetitivo de aprendizaje y es almacenado a través de la interconexión entre neuronas mediante ponderaciones (pesos) sinápticas o sinapsis. La modificación de las ponderaciones sinápticas a partir de un algoritmo de aprendizaje es lo que da lugar al proceso de aprendizaje. Toda rna tiene tres elementos fundamentales:
- •
la topología o estructura de la red, la cual determina los conjuntos de enlaces de la sinapsis;
- •
el tipo de entrenamiento, caracterizado por un sistema concentrador de las señales emitidas por cada neurona de la red, que son multiplicadas (afectadas) por la respectiva ponderación sináptica, y
- •
la regla de aprendizaje, definida por una función de activación no lineal, la cual transforma las salidas del sistema concentrador en salidas de la red neuronal.
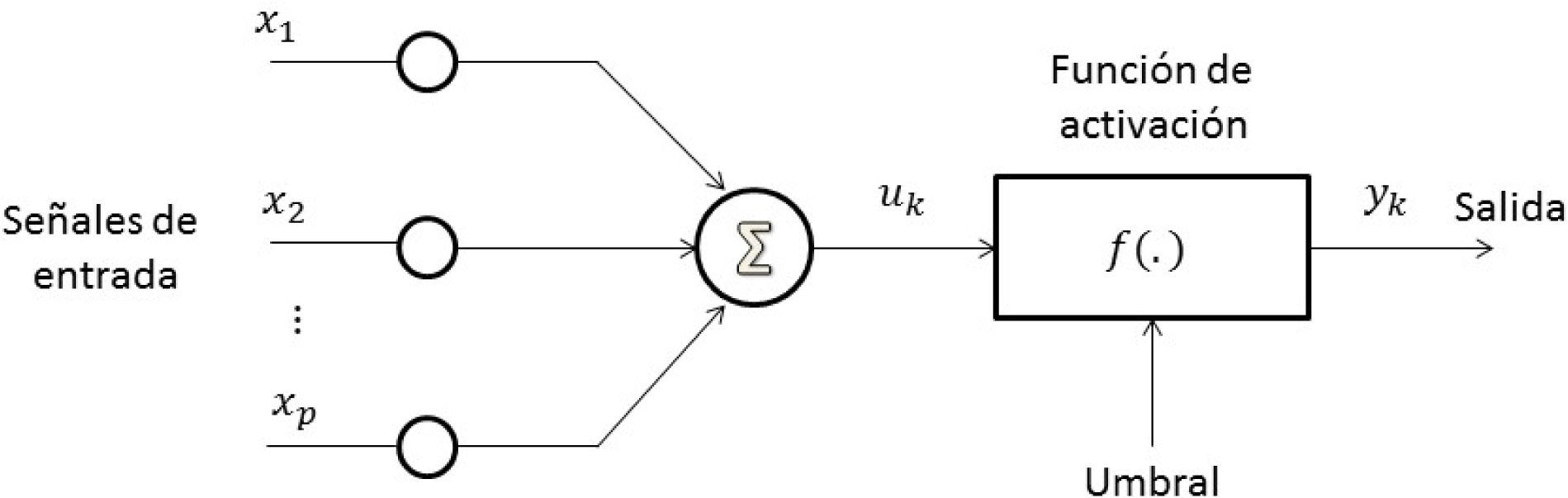
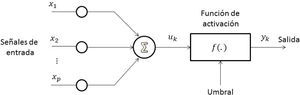
Por último, para controlar la función de activación de una rna se establece un umbral externo que funciona como un filtro de las señales que serán enviadas a la salida de la red. Siendo la neurona el elemento base de una rna, se presentan a continuación las descripciones matemática y gráfica de la i-ésima neurona de una rna:
cuya descripción gráfica se presenta en la figura 1.Modelo no lineal de una neurona
Fuente: basado en Poznyak, Sanchez y Yu (2001, p. 12).
donde uj es la j-ésima componente de la entrada; ωij es la ponderación (peso) conectada a la j-ésima componente de la neurona i; vi es la salida del sistema concentrador; ρi es el umbral; φ(.) es la función de activación no lineal, y yi es la salida de la neurona i.
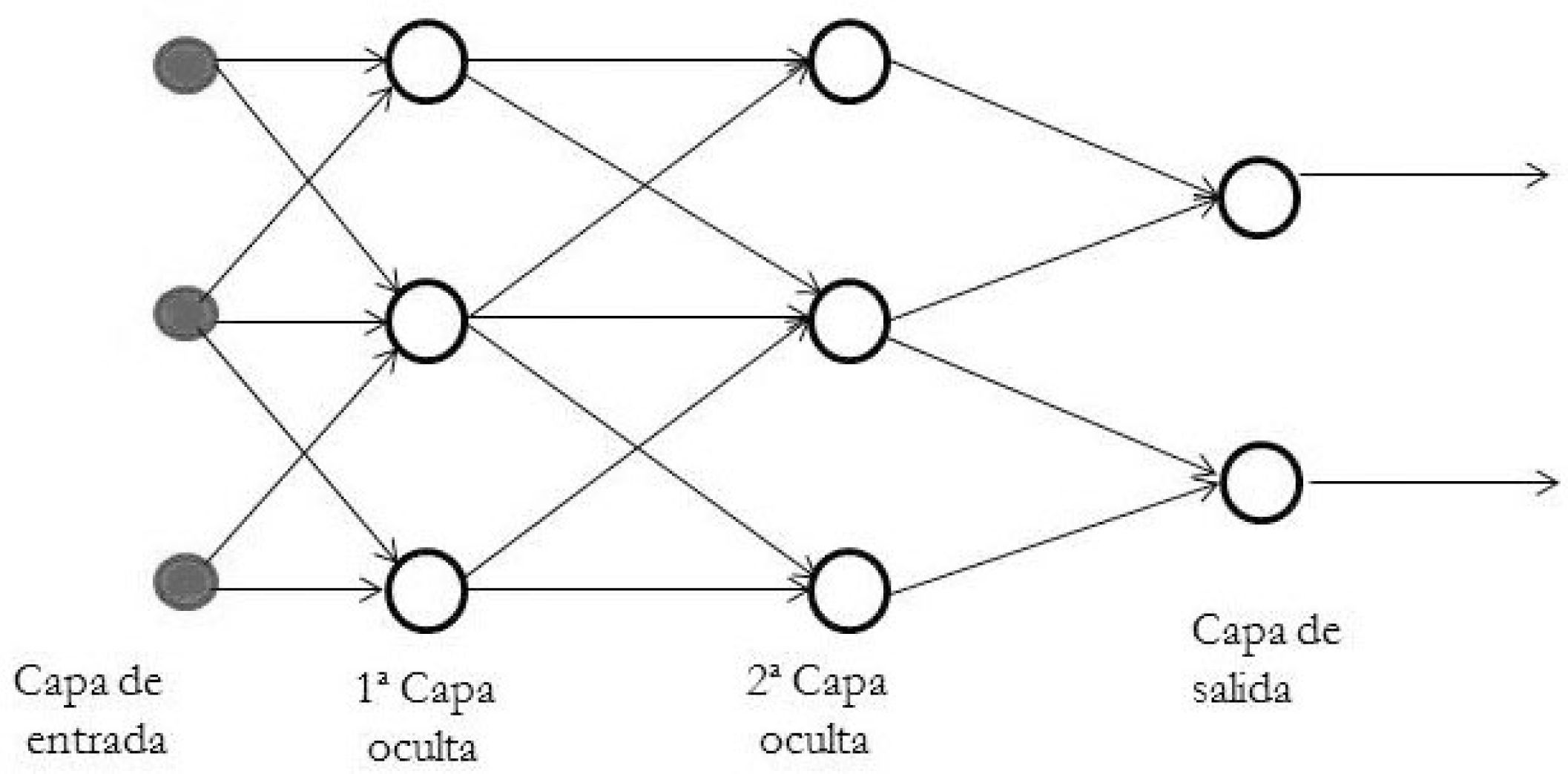
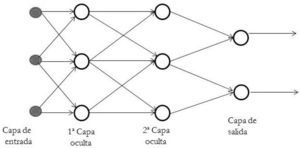
Dentro de una rna, las neuronas se agrupan en capas, por esta razón hay rna con una o más capas; los tipos de estructura de rna más empleados son cuatro: 1) red neuronal de alimentación directa de una capa o perceptrón de una capa oculta; 2) red neuronal de alimentación directa de varias capas o perceptrón multicapa; 3) redes de base radial, y 4) redes neuronales diferenciales o dinámicas en tiempo continuo.
El esquema típico de un perceptrón multicapa se muestra en la figura 2.
Perceptrón multicapa
Fuente: adaptado de Poznyak, Sanchez y Yu (2001, p. 17).
Una red neuronal diferencial se puede describir como una estructura acoplada entre un sistema identificador neuronal y un sistema controlador de seguimiento, mediante este arreglo es posible observar, registrar y analizar el comportamiento de un sistema dinámico, esto es en sí un modelo de estimación dinámica cuyo funcionamiento se basa en registrar datos de entrada, procesarlos en el sistema y proponer el siguiente valor. Dicho valor propuesto es comparado con el valor de salida del sistema; a través de esta comparación se obtiene un valor del error entre el valor propuesto (seguimiento o descripción) y el valor medido del sistema, si el error está dentro de la tolerancia se toma este valor como válido y sirve de retroalimentación al sistema, el cual generará un nuevo valor de seguimiento y así sucesivamente. En otro caso se repite el proceso modificando los pesos dentro del sistema hasta obtener un valor cuyo error con el de la salida del sistema sea el mínimo o cercano a cero, significando esto que el proceso de aprendizaje se logró alcanzar. A los resultados generados por el sistema se les denomina estados estimados del sistema.
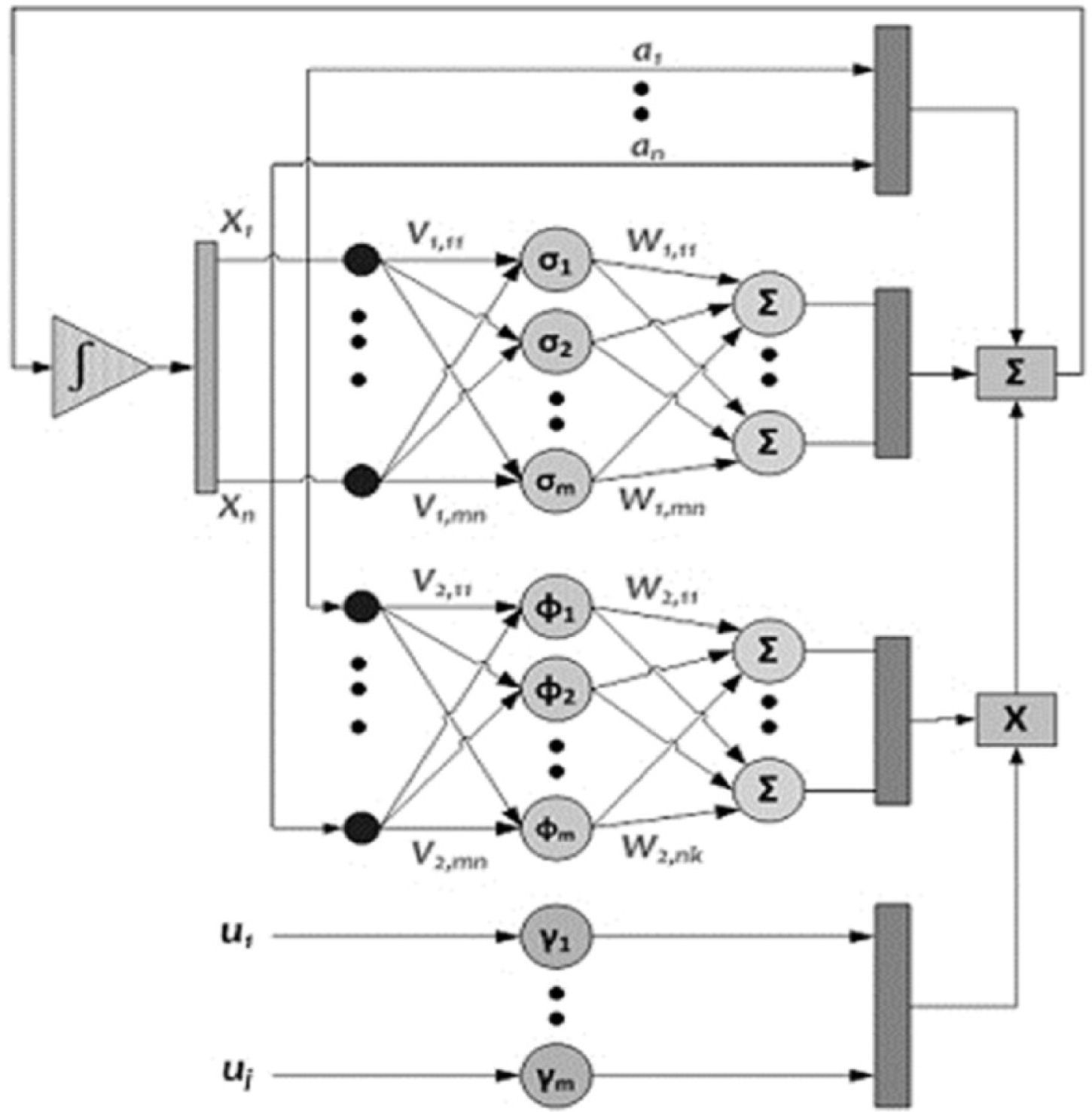
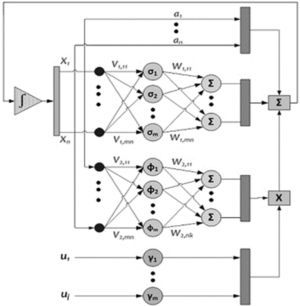
En la figura 3 se ilustra el esquema de una red neuronal diferencial típico.
Diagrama de una rnd típica
Fuente: tomada de Ortiz-Arango, Cabrera-Llanos y Venegas-Martínez (2016).
La mayoría de rnd están basadas en la estructura de una rna de Hopfield, la cual es descrita por el siguiente sistema de ecuaciones diferenciales continuas no lineales (Poznyak y Sánchez, 1999):
donde:Adicionalmente, xt es el vector de estados, con x0 conocida; xt es el vector de salida o resultados; C es la matriz de transformación del estado xt al estado yt; ξ1,t y ξ2,t son ruido blanco; ut es el vector de alimentación de información externa; W1,t∈ℝn×k es la matriz de pesos o ponderaciones de entrada, y W2,t∈ℝn×r es la matriz de pesos de retroalimentación de estados no lineales
Los valores ξ1,t y ξ2,t son ruido blanco y, aunque no pueden ser medidos a través de la dinámica del sistema, es posible acotarlos; asimismo, están asociados a los errores debido a los días no laborables en las series de tiempo (Ortiz-Arango, Cabrera-Llanos y Danvila, 2012).
En el presente trabajo se utilizó una red neuronal de una sola capa oculta, por lo cual las restricciones que debe cumplir el sistema de ecuaciones diferenciales respecto a las funciones de peso y a la forma de las funciones de activación, tanto de entrada como de retroalimentación, son las siguientes:
Por su parte, la ecuación diferencial de Riccati será:
Y el error entre el valor medido y el generado por la red es medido por:
Debe hacerse notar que la dinámica seguida por esta función de error debe ser estable en el sentido de los criterios de estabilidad de Lyapunov, lo cual supone satisfacer la ecuación [9], que garantiza la adecuada convergencia de los valores generados por la red a los valores reales. Gracias a dicha estabilidad se logra una convergencia acelerada de los valores generados por la red a los valores reales, lo que representa una gran ventaja sobre otros tipos de rna, con lo cual es posible que los valores generados por la rnd identifiquen rápidamente los cambios abruptos en la serie de tiempo analizada.
Para resolver el sistema de ecuaciones con las restricciones establecidas en las expresiones [6] a [10] se utilizó la plataforma de Matlab-Simulink®, versión 2010.
RESULTADOSEn esta sección se presentarán los resultados obtenidos mediante las dos metodologías empleadas en este análisis de los precios de cierre de barriles de petróleo wti y Brent. Los periodos analizados fueron: del 2 de enero de 2013 al 24 de febrero de 2105, que corresponde al periodo de seguimiento de la serie, y del 25 de febrero 2015 al 10 de marzo 2015, que atañe al periodo de pronóstico. Los valores de ambas series fueron obtenidos de la U.S. Energy Information Administration (eia, 2015).
A continuación se presentarán los elementos descriptivos específicos de los modelos empleados de la familia garch, posteriormente se mostrarán los resultados de los valores pronosticados mediante los modelos de la familia garch, en los cuales se utilizó el software E-Views® versión 8 para llevar a cabo los cálculos. Finalmente, se expondrán los valores pronosticados obtenidos con la rnd y se hará la comparación del error cuadrático medio entre ambos pares de series de valores pronosticados.
Para encontrar el modelo que mejor se ajustara a describir los valores previos de la serie y los valores pronosticados se probó con varios modelos de la familia garch. Después de varios intentos, se determinó que el modelo que mejor se ajustaba tanto a la descripción de los valores previos como a los pronosticados de la serie del tiempo de precios de cierre de barriles de petróleo crudo del tipo Brent fue un modelo tgarch(1,1), el cual está definido por las siguientes expresiones y parámetros:
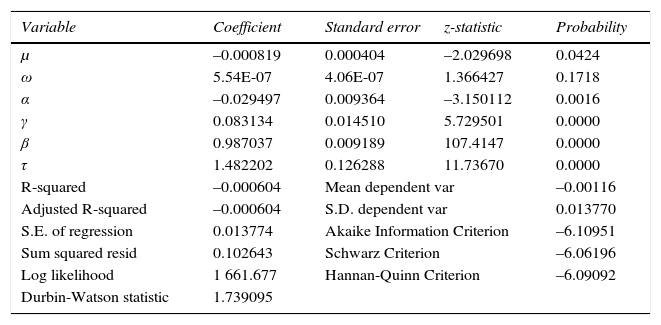
A partir de los cuales se obtuvo la distribución general de errores del modelo tgarch(1,1) para los precios de crudo Brent, expresados en el cuadro 1.
Elementos estadísticos descriptivos del modelo tgarch(1,1) de la serie de precios de cierre de barriles de petróleo Brent
| Variable | Coefficient | Standard error | z-statistic | Probability |
|---|---|---|---|---|
| μ | –0.000819 | 0.000404 | –2.029698 | 0.0424 |
| ω | 5.54E-07 | 4.06E-07 | 1.366427 | 0.1718 |
| α | –0.029497 | 0.009364 | –3.150112 | 0.0016 |
| γ | 0.083134 | 0.014510 | 5.729501 | 0.0000 |
| β | 0.987037 | 0.009189 | 107.4147 | 0.0000 |
| τ | 1.482202 | 0.126288 | 11.73670 | 0.0000 |
| R-squared | –0.000604 | Mean dependent var | –0.00116 | |
| Adjusted R-squared | –0.000604 | S.D. dependent var | 0.013770 | |
| S.E. of regression | 0.013774 | Akaike Information Criterion | –6.10951 | |
| Sum squared resid | 0.102643 | Schwarz Criterion | –6.06196 | |
| Log likelihood | 1 661.677 | Hannan-Quinn Criterion | –6.09092 | |
| Durbin-Watson statistic | 1.739095 | |||
Del mismo modo, para el caso de los precios de cierre de barriles de petróleo wti, después de realizar diferentes pruebas, se encontró que el modelo de la familia garch que mejor se ajustaba a describir los valores pasados y efectuar un pronóstico fue un modelo garch(1,1), el cual está determinado por el siguiente grupo de ecuaciones y parámetros:
Cuya distribución t de los errores de este modelo garch(1,1) está descrita en el cuadro 2.
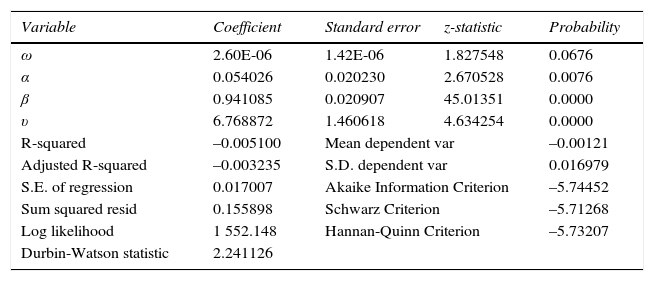
Elementos estadísticos descriptivos del modelo garch(1,1) de la serie de precios de cierre de barriles de petróleo wti
| Variable | Coefficient | Standard error | z-statistic | Probability |
|---|---|---|---|---|
| ω | 2.60E-06 | 1.42E-06 | 1.827548 | 0.0676 |
| α | 0.054026 | 0.020230 | 2.670528 | 0.0076 |
| β | 0.941085 | 0.020907 | 45.01351 | 0.0000 |
| υ | 6.768872 | 1.460618 | 4.634254 | 0.0000 |
| R-squared | –0.005100 | Mean dependent var | –0.00121 | |
| Adjusted R-squared | –0.003235 | S.D. dependent var | 0.016979 | |
| S.E. of regression | 0.017007 | Akaike Information Criterion | –5.74452 | |
| Sum squared resid | 0.155898 | Schwarz Criterion | –5.71268 | |
| Log likelihood | 1 552.148 | Hannan-Quinn Criterion | –5.73207 | |
| Durbin-Watson statistic | 2.241126 | |||
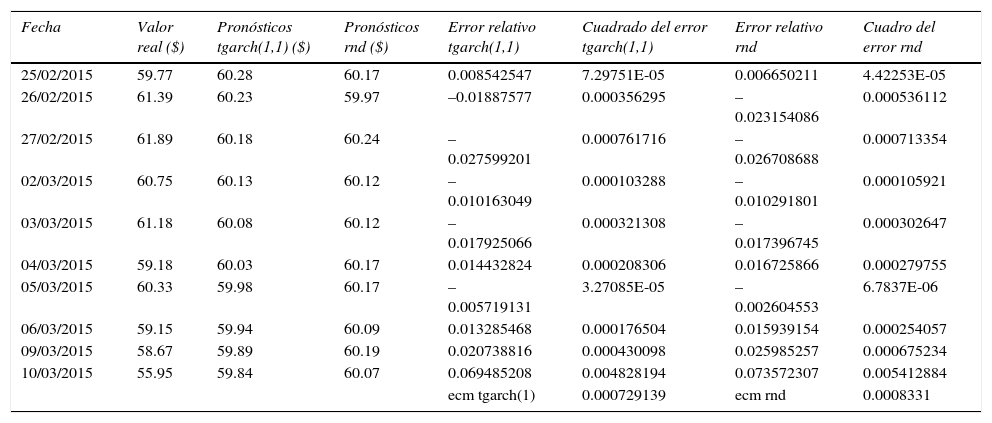
A continuación, en el cuadro 3, se presenta la comparación de los pronósticos obtenidos para la serie de precios del barriles de crudo Brent empleando el modelo basado en rnd y los obtenidos mediante el modelo tgarch(1,1). En el cuadro 4 se lleva a cabo la misma comparación para la serie de precios de barriles de crudo wti, modelo rnd contra el modelo garch(1,1). En ambos casos para el periodo del 25 de febrero al 10 de marzo de 2015.
Comparación de valores reales precio por barril de crudo Brent vs. pronósticos tgarch(1,1) vs. pronósticos con rnd
| Fecha | Valor real ($) | Pronósticos tgarch(1,1) ($) | Pronósticos rnd ($) | Error relativo tgarch(1,1) | Cuadrado del error tgarch(1,1) | Error relativo rnd | Cuadro del error rnd |
|---|---|---|---|---|---|---|---|
| 25/02/2015 | 59.77 | 60.28 | 60.17 | 0.008542547 | 7.29751E-05 | 0.006650211 | 4.42253E-05 |
| 26/02/2015 | 61.39 | 60.23 | 59.97 | –0.01887577 | 0.000356295 | –0.023154086 | 0.000536112 |
| 27/02/2015 | 61.89 | 60.18 | 60.24 | –0.027599201 | 0.000761716 | –0.026708688 | 0.000713354 |
| 02/03/2015 | 60.75 | 60.13 | 60.12 | –0.010163049 | 0.000103288 | –0.010291801 | 0.000105921 |
| 03/03/2015 | 61.18 | 60.08 | 60.12 | –0.017925066 | 0.000321308 | –0.017396745 | 0.000302647 |
| 04/03/2015 | 59.18 | 60.03 | 60.17 | 0.014432824 | 0.000208306 | 0.016725866 | 0.000279755 |
| 05/03/2015 | 60.33 | 59.98 | 60.17 | –0.005719131 | 3.27085E-05 | –0.002604553 | 6.7837E-06 |
| 06/03/2015 | 59.15 | 59.94 | 60.09 | 0.013285468 | 0.000176504 | 0.015939154 | 0.000254057 |
| 09/03/2015 | 58.67 | 59.89 | 60.19 | 0.020738816 | 0.000430098 | 0.025985257 | 0.000675234 |
| 10/03/2015 | 55.95 | 59.84 | 60.07 | 0.069485208 | 0.004828194 | 0.073572307 | 0.005412884 |
| ecm tgarch(1) | 0.000729139 | ecm rnd | 0.0008331 |
Fuente: elaboración propia con datos de eia (2015).
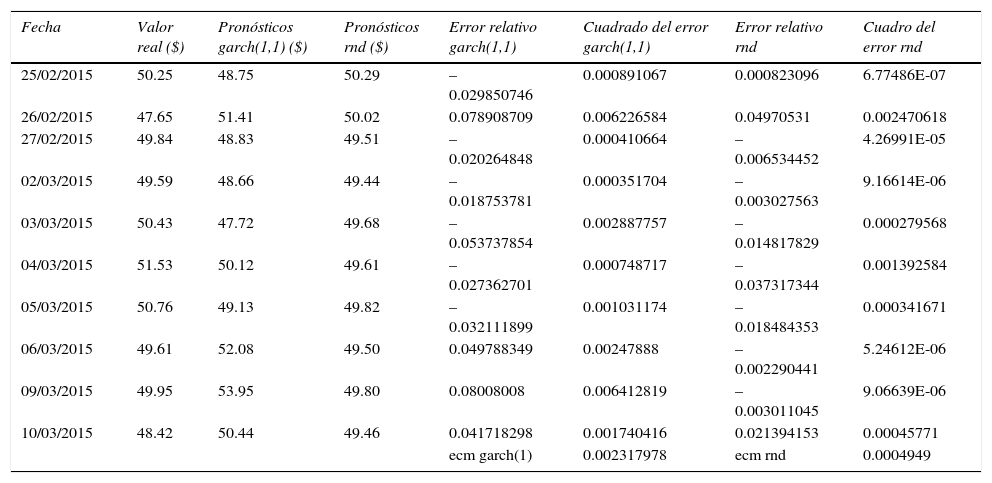
Comparación de valores reales de precio por barril de crudo wti vs. pronósticos garch(1,1) vs. pronósticos con rnd
| Fecha | Valor real ($) | Pronósticos garch(1,1) ($) | Pronósticos rnd ($) | Error relativo garch(1,1) | Cuadrado del error garch(1,1) | Error relativo rnd | Cuadro del error rnd |
|---|---|---|---|---|---|---|---|
| 25/02/2015 | 50.25 | 48.75 | 50.29 | –0.029850746 | 0.000891067 | 0.000823096 | 6.77486E-07 |
| 26/02/2015 | 47.65 | 51.41 | 50.02 | 0.078908709 | 0.006226584 | 0.04970531 | 0.002470618 |
| 27/02/2015 | 49.84 | 48.83 | 49.51 | –0.020264848 | 0.000410664 | –0.006534452 | 4.26991E-05 |
| 02/03/2015 | 49.59 | 48.66 | 49.44 | –0.018753781 | 0.000351704 | –0.003027563 | 9.16614E-06 |
| 03/03/2015 | 50.43 | 47.72 | 49.68 | –0.053737854 | 0.002887757 | –0.014817829 | 0.000279568 |
| 04/03/2015 | 51.53 | 50.12 | 49.61 | –0.027362701 | 0.000748717 | –0.037317344 | 0.001392584 |
| 05/03/2015 | 50.76 | 49.13 | 49.82 | –0.032111899 | 0.001031174 | –0.018484353 | 0.000341671 |
| 06/03/2015 | 49.61 | 52.08 | 49.50 | 0.049788349 | 0.00247888 | –0.002290441 | 5.24612E-06 |
| 09/03/2015 | 49.95 | 53.95 | 49.80 | 0.08008008 | 0.006412819 | –0.003011045 | 9.06639E-06 |
| 10/03/2015 | 48.42 | 50.44 | 49.46 | 0.041718298 | 0.001740416 | 0.021394153 | 0.00045771 |
| ecm garch(1) | 0.002317978 | ecm rnd | 0.0004949 |
Fuente: elaboración propia con datos de eia (2015).
Como puede apreciarse en el cuadro 3, el pronóstico realizado con el modelo tgarch(1,1) para el precio del crudo Brent mostró un desempeño ligeramente superior al calculado con el modelo de rnd, lo cual se puede comprobar al comparar el error cuadrático medio (ecm) de ambas series de pronósticos, para el caso del modelo tgarch(1,1), ecm = 0.000729139, y para el modelo con rnd, ecm = 0.0008331, es decir, una diferencia de 0.000103958, poco más de un diezmilésimo en el ecm.
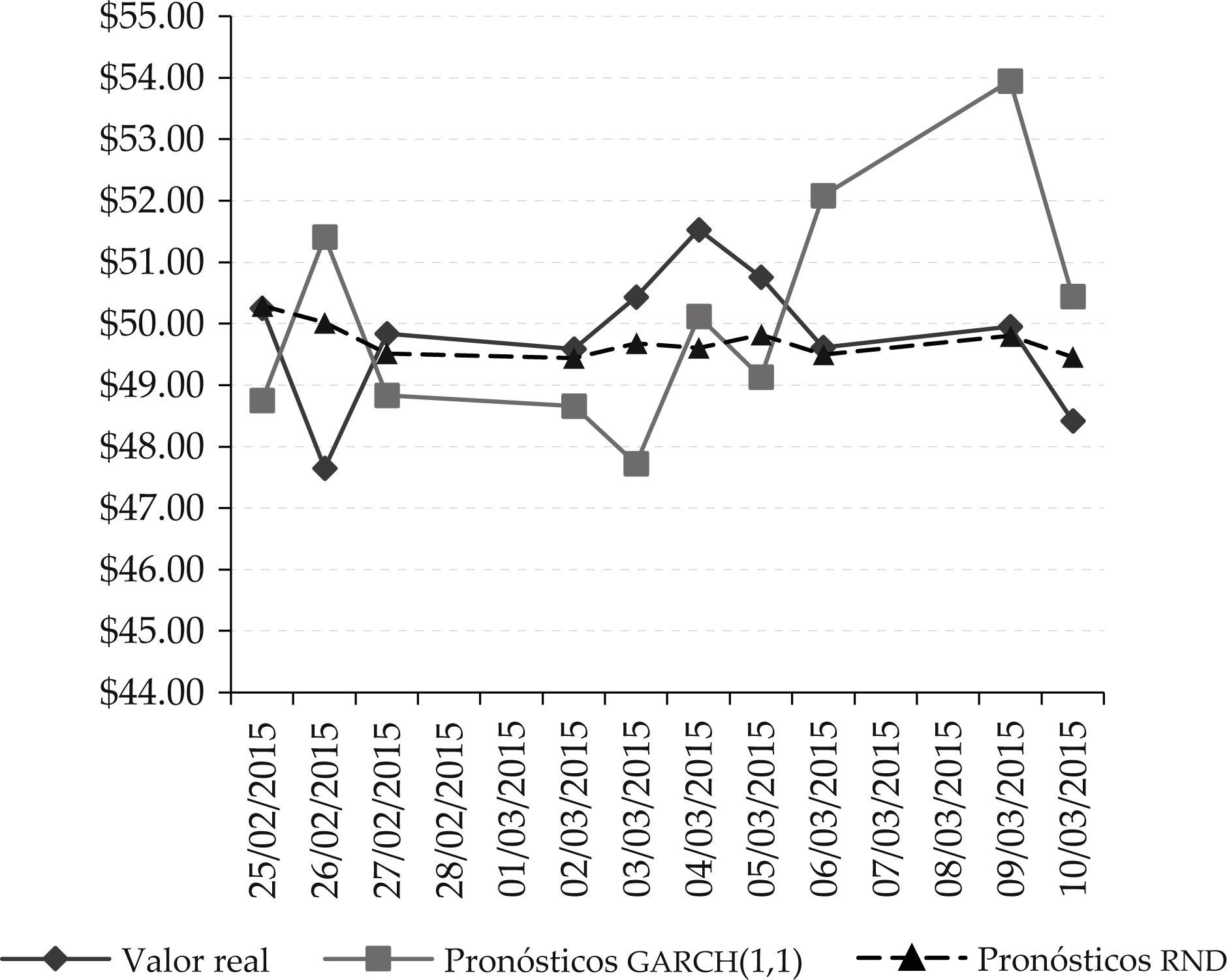
Por otro lado, en el caso del pronóstico de precios del crudo wti, el cuadro 4 muestra que el desempeño del modelo basado en rnd fue muy superior al del modelo garch(1,1), pues para el caso del modelo garch(1,1), ecm = 0.002317978, y para el modelo de rnd, ecm = 0.0004949, lo cual representa una diferencia en el ecm de 0.001823078, poco más de 18 diezmilésimos.
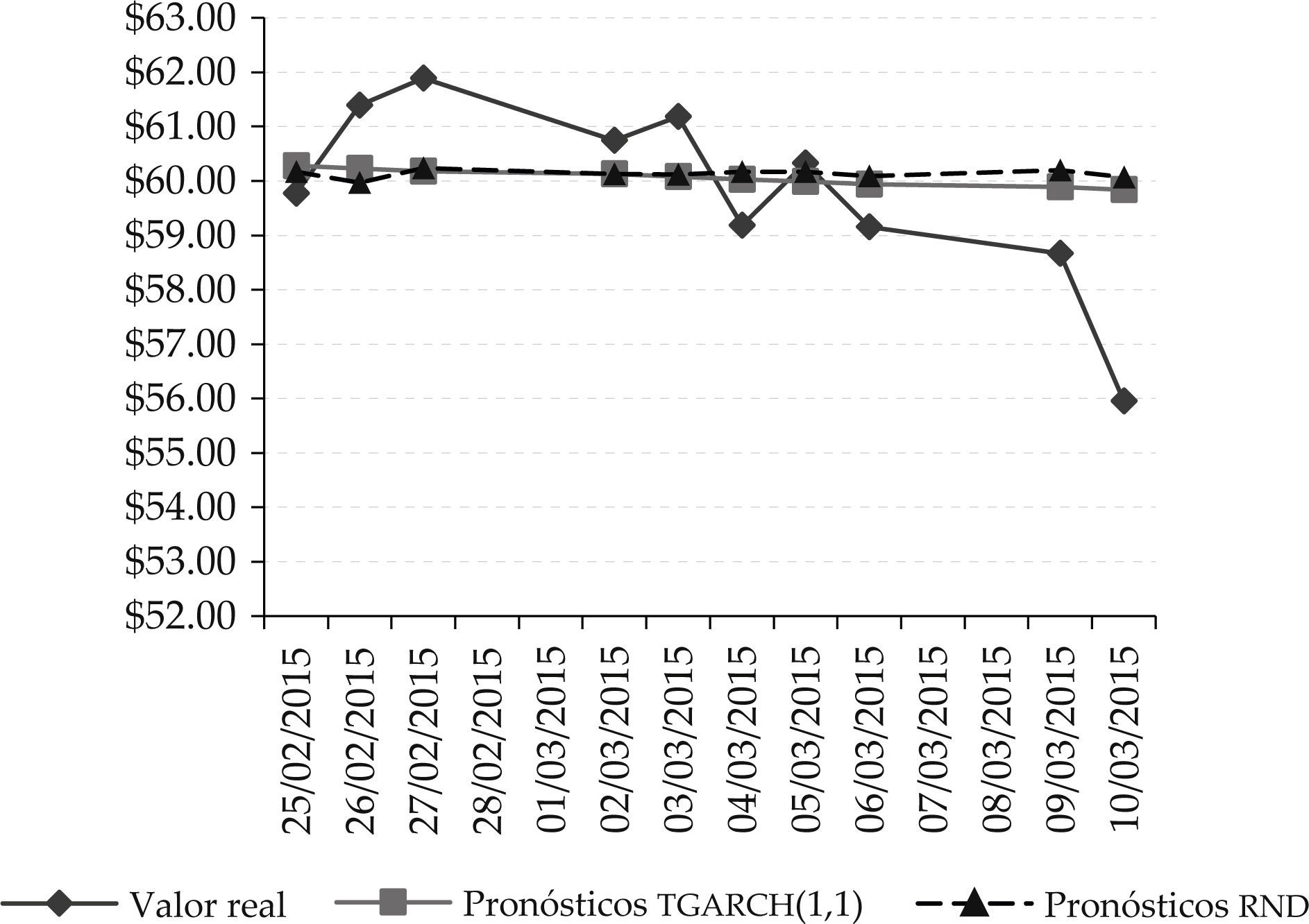
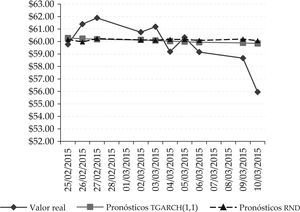
Lo anterior se puede apreciar mejor en las gráficas 1 y 2, en las cuales se muestran las comparaciones de los valores reales versus los valores pronosticados por ambos modelos de la familia garch y el modelo de rnd, para ambos tipos de petróleo crudo.
Precios de cierre de barriles de petróleo Brent reales vs. pronosticados mediante modelo tgarch(1,1) vs. rnd
Fuente: elaboración propia con datos de eia (2015).
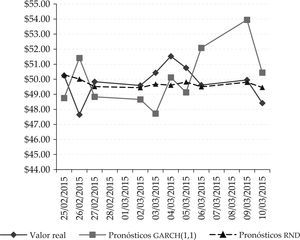
Precios de cierre de barriles de petróleo wti reales vs. pronosticados mediante modelo garch(1,1) vs. rnd
Fuente: elaboración propia con datos de eia (2015).
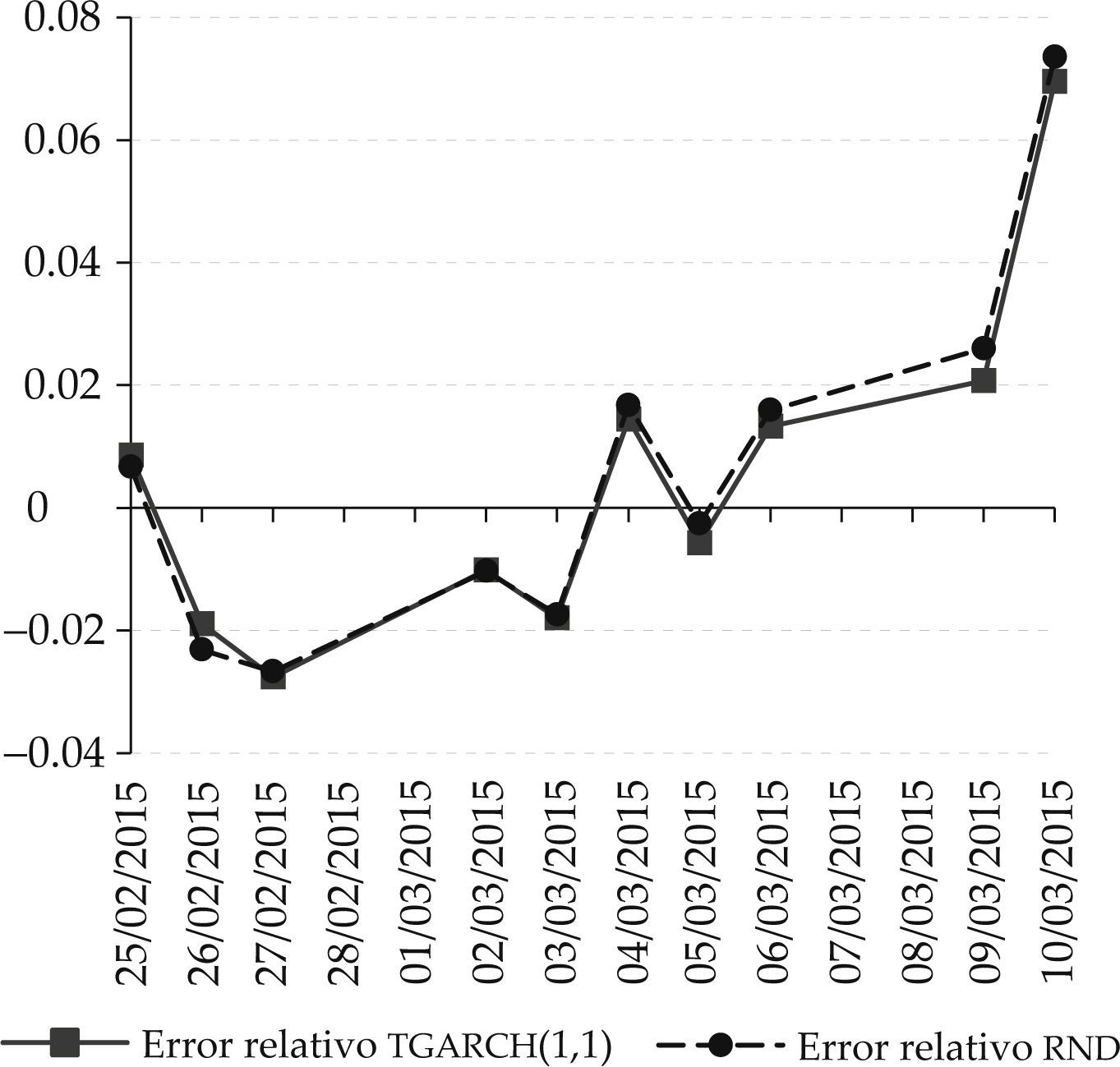
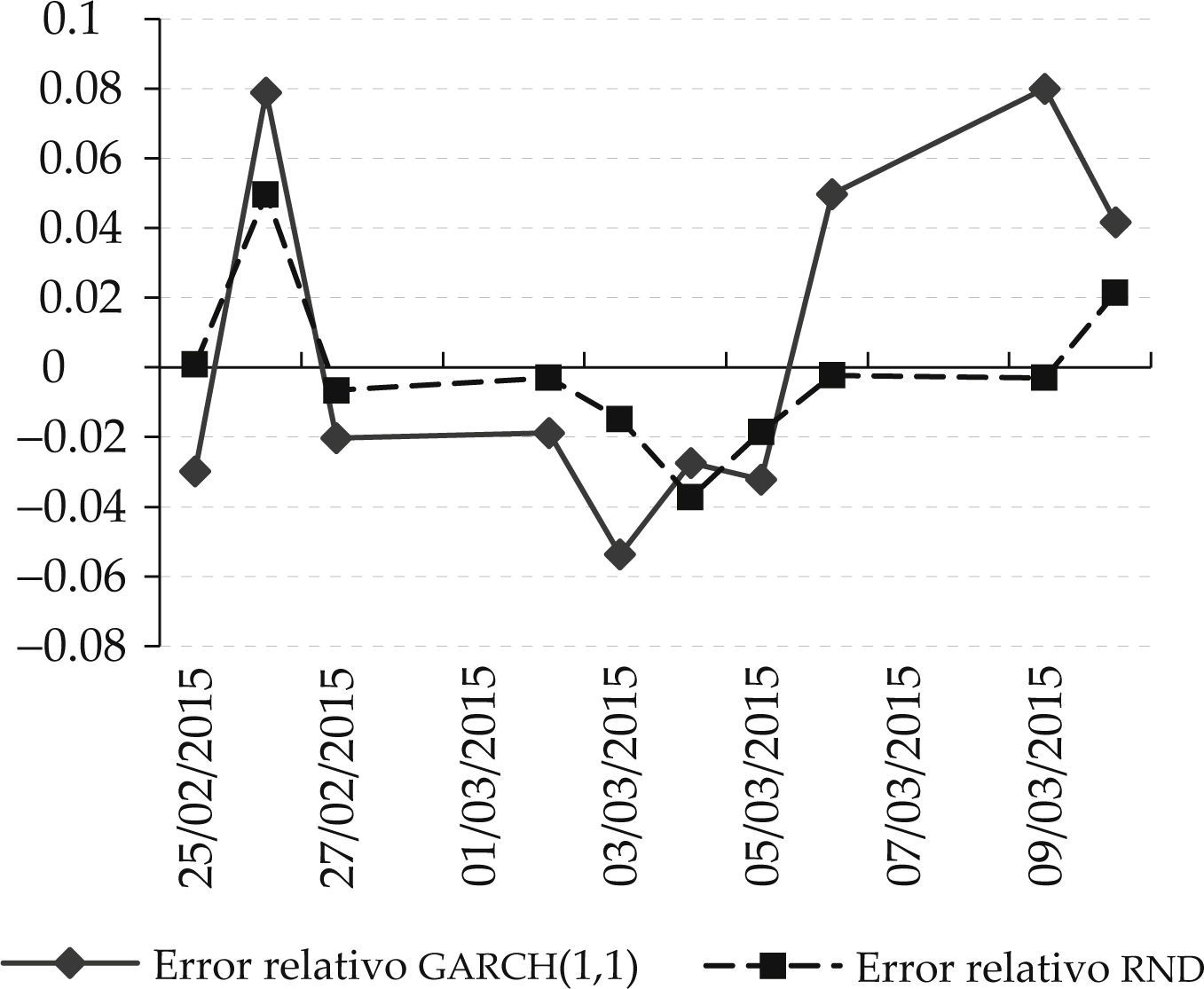
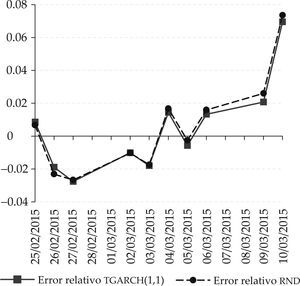
Como complemento, en las gráficas 3 y 4 se muestra respectivamente el comportamiento del ecm de ambos pares de series usando tgarch(1,1) versusrnd y garch(1,1) versusrnd.
ecm de pronósticos de precio de barriles de petróleo Brent mediante modelo tgarch(1,1) vs. rnd
Fuente: elaboración propia con datos de eia (2015).
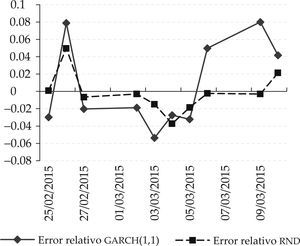
ecm de pronósticos de precio de barriles de petróleo wti mediante modelo garch (1,1) vs. rnd
Fuente: elaboración propia con datos de eia (2015).
Como puede apreciarse del análisis anterior, los pronósticos obtenidos mediante el modelo de rnd son un poco menos precisos que los obtenidos a través del modelo tgarch(1,1) para el caso de los precios de petróleo crudo Brent, y considerablemente más precisos que los obtenidos mediante el modelo garch(1,1) para los precios de petróleo crudo wti.
CONCLUSIONESMediante el análisis de las series de precios de cierre de los precios de barriles de petróleo crudo de los tipos Brent y wti se pudo comprobar que las redes neuronales diferenciales pueden ser adoptadas como una técnica de cálculo de pronósticos comparable, e incluso superior en su desempeño, a las técnicas basadas en modelos de la familia garch, los cuales han venido predominando desde inicios de la década de los noventa para llevar a cabo análisis de series de tiempo que presentan comportamientos no lineales debido a efectos de la volatilidad.
El uso de un modelo de rnd para llevar a cabo pronósticos de valores futuros de una serie de tiempo no lineal es mucho más simple que realizar pronósticos mediante modelos de la familia garch; en los casos analizados fue bastante laborioso identificar cuál de los modelos de la familia garch era más preciso en el cálculo de valores futuros, pues se tuvieron que hacer distintas pruebas sobre el comportamiento de la serie, probar con varios de los modelos de esta familia y, con base en los resultados, determinar cuál de estos proporcionaba pronósticos más precisos. En el caso de la rnd solamente se usa un solo modelo, al cual se alimenta con los valores históricos y se van ajustando sus valores hasta llegar al valor buscado, de acuerdo al criterio de convergencia de Lyapunov.
En trabajos futuros se llevarán a cabo comparaciones similares con otras series de tiempo financieras y se espera que consoliden la propuesta establecida en el presente trabajo.