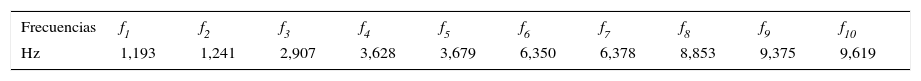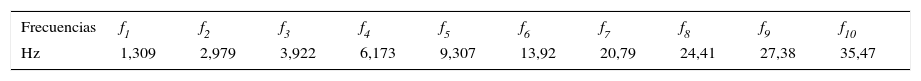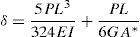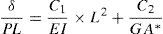ACCIONA Infraestructuras ha construido un faro de 32m de altura fabricado en Madrid íntegramente con polímeros reforzados con fibra (PRF) e instalado en solo 2h en la ampliación norte del puerto de Valencia en febrero de 2015. Una vez instalado el faro, las vibraciones de la estructura inducidas por el viento se registraron por medio de una serie de acelerómetros colocados estratégicamente para determinar su respuesta dinámica. Previamente, se llevó a cabo una simulación numérica de la estructura para determinar sus frecuencias naturales y formas modales, comparándolas con las obtenidas de manera experimental.
A 32-metre high lighthouse, made entirely with fibre reinforced polymers (FRPs), was manufactured by ACCIONA Infrastructure in Madrid, and was installed in only two hours in the northern extension of the Port of Valencia in February 2015. Once the FRP lighthouse was installed, its wind induced vibrations were recorded by a set of accelerometers, strategically placed to determine its dynamic response. Previously, a numerical simulation of the structure was performed to assess its natural frequencies and mode shapes, and compare them with those determined experimentally.
En ambientes agresivos, como en las zonas costeras y portuarias, una alternativa atractiva y prometedora a los materiales tradicionales (como el acero o el hormigón armado con acero) para minimizar los costes de mantenimiento de las estructuras civiles es el uso de materiales duraderos y ligeros, como los polímeros reforzados con fibra (PRF). ACCIONA Construcción es pionera en el uso de estos materiales en obras de ingeniería civil, como puentes [1], pasarelas [2,3], estructuras de hormigón armado con barras de PRF [4], etc. Debido al particular comportamiento mecánico de las estructuras de PRF y al creciente interés en esta tecnología, en los últimos años se han llevado a cabo numerosos proyectos de investigación tanto desde el punto de vista experimental como numérico, la mayoría de ellos centrados en la respuesta estática de las estructuras de PRF, pero muy pocos en el campo de la respuesta dinámica [5,6]. En el caso del faro de PRF presentado en este trabajo, la rigidez de los elementos estructurales tiene una influencia importante en la respuesta dinámica de la estructura, por lo que puede calibrarse un modelo numérico adecuado a partir de los resultados experimentales de la respuesta a vibraciones libres de la estructura.
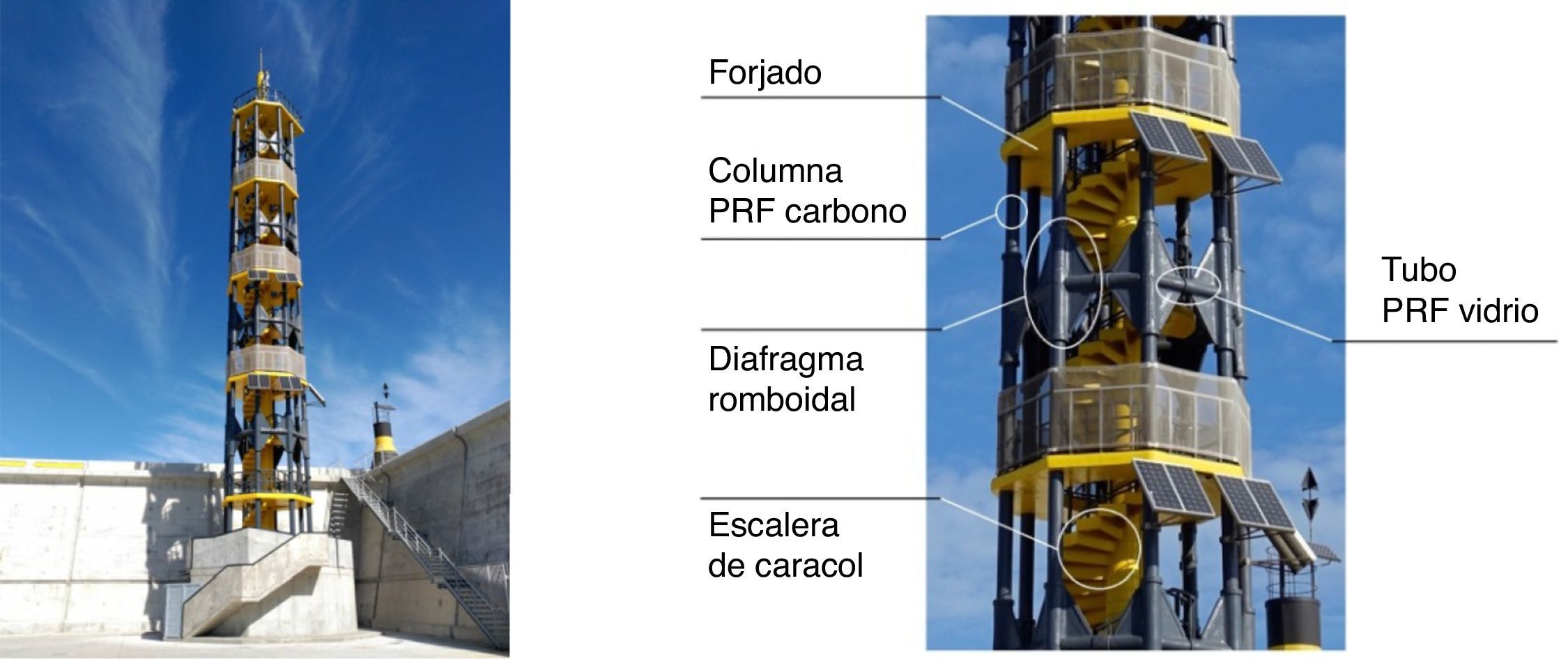
2Descripción de la estructuraEl nuevo faro de PRF (fig. 1) es una estructura de 32m de altura formada por 5 forjados que apoyan sobre 8 columnas de PRF de carbono cuyos ejes centrales, en el forjado inferior (F1), atraviesan los vértices de un octágono inscrito en una circunferencia de 4,15m de diámetro, y en el forjado superior (F5), los vértices de un octágono inscrito en una circunferencia de 3,75m de diámetro. Estas columnas de 32m de altura son tubos circulares fabricados por pultrusión con resina epoxi (fig. 2a), tienen un diámetro exterior de 250mm y un espesor de pared del tubo de 20mm. Los 5 forjados, fabricados por infusión de resina viniléster (fig. 2b), son paneles tipo sándwich de 200mm de espesor, con pieles de PRF de vidrio de 10mm de espesor y un núcleo de poliuretano con una densidad de 70kg/m3. Los forjados se ubican distanciados en altura cada 6m, y cada uno tiene una geometría octagonal diferente dependiendo de su posición en la estructura.
En el centro de la estructura, desde la base hasta el forjado superior, se dispone una escalera de caracol. Los peldaños de la escalera están fabricados mediante el proceso de moldeo por inyección de resina (RTM) y tienen una estructura sándwich con pieles de PRF de vidrio y núcleo de poliuretano (fig. 2c). Cada peldaño tiene una altura de 200mm y está formado por un anillo con un diámetro interno de 500mm unido a una plataforma trapezoidal de 900mm de longitud, con un ancho de huella variable. Los anillos de los peldaños, alineados verticalmente a lo largo del eje central del faro, forman un hueco cilíndrico que está relleno de hormigón armado, proporcionando así un núcleo de rigidización a la estructura.
Para aumentar la rigidez lateral de la estructura, las columnas de PRF de carbono están conectadas entre sí por 4 anillos octagonales colocados de manera equidistante entre cada 2 forjados consecutivos. Cada uno de estos anillos está formado por 8 tubos de PRF de vidrio dispuestos perimetralmente a la estructura. Los tubos de PRF de vidrio, fabricados por pultrusión, tienen un diámetro exterior de 190mm y un espesor de pared del tubo de 20mm. Las conexiones entre las columnas y los tubos horizontales de PRF de vidrio se realizan mediante diafragmas de PRF con forma romboidal y que tienen un espesor de 42mm (fig. 2d).
La base del faro es un cajón de hormigón armado de 4m de altura con forma prismática octagonal. Los extremos inferiores de las columnas del faro están empotrados en la losa inferior del cajón, de 1,10m de espesor. La losa de hormigón armado de 0,35m que forma el techo del cajón presenta unas perforaciones para permitir el paso de las 8 columnas de PRF de carbono y del núcleo central de hormigón armado. Entre las columnas de PRF y esta losa de hormigón, se disponen unos collarines de neopreno para restringir el desplazamiento horizontal de las columnas en este nivel.
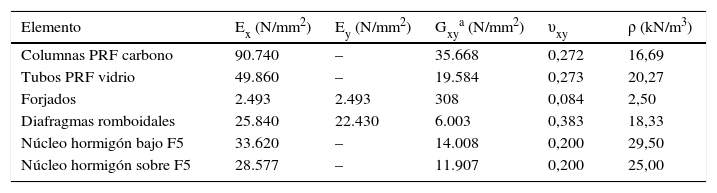
3Simulación numérica3.1Descripción del modelo numéricoSe ha realizado un modelo tridimensional de toda la estructura utilizando el programa de cálculo mediante elementos finitos SAP-2000 v16.1.1. Las columnas de PRF de carbono, los tubos de PRF de vidrio y la columna central de hormigón armado se modelan con elementos tipo barra, mientras que los forjados y los diafragmas romboidales se modelan con elementos tipo placa. Cada columna está fijada en su base, mientras que su contacto con la losa superior del cajón de hormigón se modela mediante un conjunto de muelles elásticos lineales conectados radialmente a los elementos tipo barra de las columnas y que tienen una rigidez equivalente a la del collarín de neopreno. Cada elemento estructural se caracteriza por los parámetros elásticos (Ex, Ey, Gxy y νxy) y el peso específico tomados de la tabla 1. Aunque las columnas de PRF de carbono y los tubos de PRF de vidrio están fabricados con materiales ortótropos, el módulo elástico transversal Ey no se utiliza en el modelo, ya que estas piezas se modelan con elementos tipo barra. Los peldaños de la escalera de caracol no se han modelado, ya que se supone que no contribuyen a la rigidez de la estructura. Sin embargo, sus masas se han considerado añadiéndolas a los elementos tipo barra que modelan el núcleo central de hormigón por debajo del forjado F5.
Parámetros de los elementos estructurales
| Elemento | Ex (N/mm2) | Ey (N/mm2) | Gxya (N/mm2) | υxy | ρ (kN/m3) |
|---|---|---|---|---|---|
| Columnas PRF carbono | 90.740 | – | 35.668 | 0,272 | 16,69 |
| Tubos PRF vidrio | 49.860 | – | 19.584 | 0,273 | 20,27 |
| Forjados | 2.493 | 2.493 | 308 | 0,084 | 2,50 |
| Diafragmas romboidales | 25.840 | 22.430 | 6.003 | 0,383 | 18,33 |
| Núcleo hormigón bajo F5 | 33.620 | – | 14.008 | 0,200 | 29,50 |
| Núcleo hormigón sobre F5 | 28.577 | – | 11.907 | 0,200 | 25,00 |
Se realiza un análisis modal del modelo numérico de la estructura para obtener los modos de vibración y las frecuencias correspondientes, con el objetivo de compararlos con los medidos experimentalmente. Las frecuencias correspondientes a los primeros 10 modos de vibración en el modelo numérico se presentan en la tabla 2.
4Análisis experimental4.1Ensayos estáticos de los elementos estructuralesLas propiedades mecánicas de resistencia y rigidez de cada elemento se determinan experimentalmente mediante pruebas estáticas.
4.1.1Ensayos de flexión hasta roturaPara determinar la resistencia a flexión de los tubos de PRF de carbono y de PRF de vidrio que forman la estructura del faro, se realiza un ensayo de flexión a 3 puntos hasta rotura con una muestra de cada uno de los tubos, con 6 y 4m de distancia entre apoyos en cada caso, respectivamente. En la figura 3 se muestran estos 2 ensayos hasta rotura.
El momento resistente del tubo de PRF de vidrio es de MR,FV=208,3kNm, mientras que el momento resistente del tubo de PRF de carbono es de MFC=385,5kNm. Estos valores experimentales de resistencia son muy superiores a los valores de diseño utilizados para la estructura, ya que el parámetro condicionante en el diseño del faro es la rigidez de sus elementos estructurales.
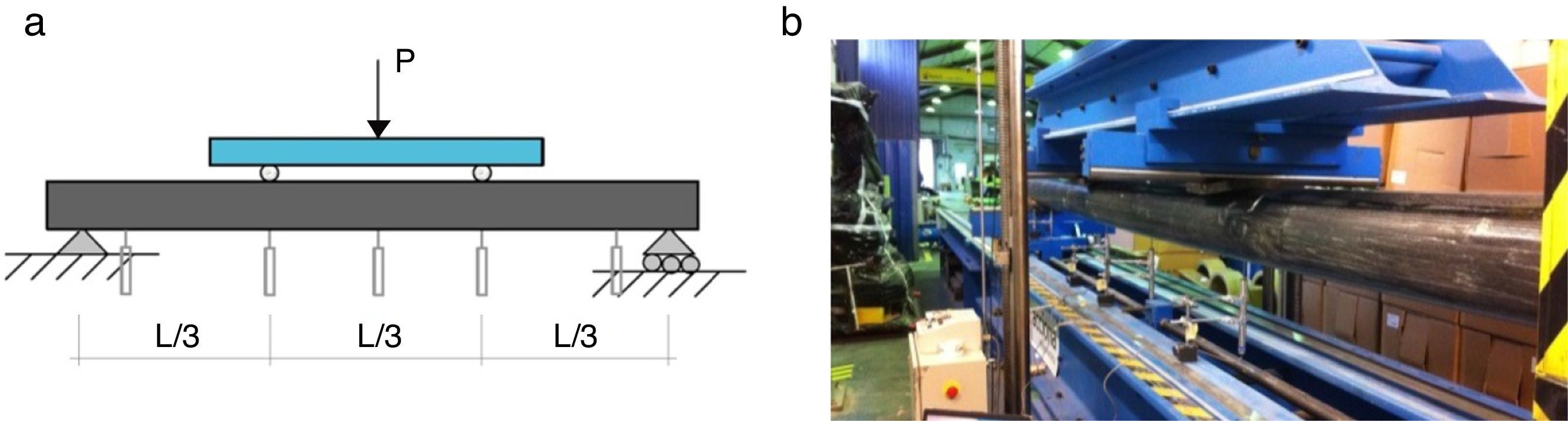
4.1.2Ensayos de flexión a diferentes distancias entre apoyosPara una correcta evaluación numérica del comportamiento dinámico del faro de PRF, es necesario conocer de manera precisa el parámetro EI (rigidez a flexión) de los tubos de PRF de carbono a utilizar en el modelo numérico. Sin embargo, la determinación experimental de EI mediante ensayos a flexión de elementos de PRF suele verse afectada por la presencia de una considerable deformación por cortante, debido en este caso al reducido valor del módulo de cortante G de los PRF, obteniendo en dicho caso una rigidez a flexión aparente inferior a la real. Para reducir o eliminar el efecto del cortante en la determinación de la rigidez a flexión de los tubos de PRF de carbono, se han realizado ensayos a 4 puntos (con puntos de aplicación de la carga a L/3) con diferentes distancias L entre apoyos (fig. 4). Este método se basa en la teoría de flexión de vigas de Timoshenko [7] y en la aproximación utilizada por Bank [8] para vigas de PRF. Para esta configuración de ensayo a flexión, el desplazamiento vertical del tubo bajo los puntos de aplicación de la carga, según la ecuación de Timoshenko, viene dada por la expresión:
Dividiendo los términos de la ecuación (1) por PL, se tiene que:
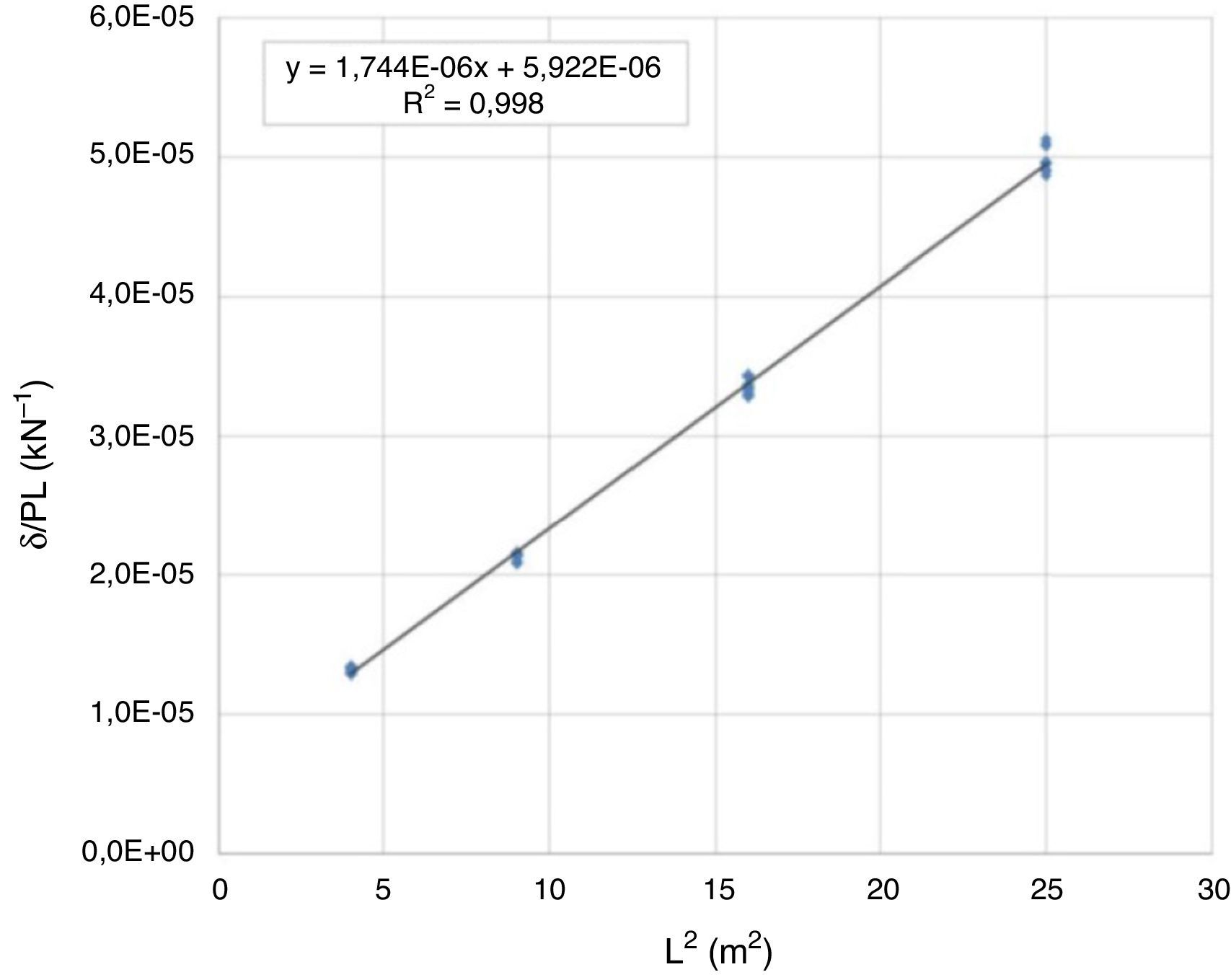
La ecuación (2) sería la ecuación de una recta con δ/PL la variable dependiente y L2 la variable independiente. Conocidos los valores de carga-desplazamiento P/δ y el vano L de cada ensayo, se puede dibujar dicha recta, cuya pendiente y ordenada en el origen son inversamente proporcionales a la rigidez a flexión EI y la rigidez a cortante GA*, respectivamente. Para esta configuración de ensayo, los parámetros considerados han sido C1=5/324 y C2=1/6. Para el área de cortante A* se ha adoptado un valor del 50% del área de la sección transversal del tubo.
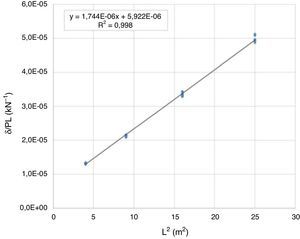
Se han realizado 4 ensayos para cada una de las 4 diferentes distancias L entre apoyos que se han analizado: 2, 3, 4 y 5m, resultando en un total de 16 ensayos a flexión. Representando para cada hipótesis de carga el valor de δ/PL frente a L2 en el punto de máxima carga durante el ensayo (que se corresponde con un valor de carga muy inferior al de rotura del tubo, es decir, el material se encuentra en régimen elástico), se obtiene una recta (fig. 5), a partir de cuya pendiente (a=1,74410−6) se calcula el módulo de Young E, obteniendo el valor de E=91.904MPa, solo un 1% superior al valor teórico (tabla 1) utilizado en el modelo numérico. Por su parte, a partir de la ordenada en el origen (b=5,92210−6) se obtiene el valor experimental del módulo de cortante G=3.895MPa, un orden de magnitud inferior al valor utilizado en el modelo numérico (tabla 1).
4.2Prueba dinámica de la estructuraEn mayo de 2015, 3 meses después de la instalación del faro, se registran las vibraciones inducidas por el viento en la estructura mediante un conjunto de acelerómetros estratégicamente colocados para determinar su respuesta dinámica. Se utilizan 8 acelerómetros unidireccionales DeltaTron Tipo 4508, conectados a su correspondiente adquisidor de datos Brüel & Kjær LAN-XI 51,2kHz - Tipo 3050. En cada forjado, excepto en el más bajo (F1), se colocan 2 acelerómetros unidireccionales, uno orientado a lo largo del eje X y el otro orientado a lo largo del eje Y (fig. 6).
En los forjados F3, F4 y F5, cada par de acelerómetros se fija a un bloque de acero de 5kg situado sobre la superficie superior del forjado cerca de una de las columnas de PRF de carbono, tal y como se muestra en la figura 6a. En el forjado F2 los acelerómetros están fijados a unos pequeños perfiles en L unidos a la superficie superior del forjado cerca de la columna central de la estructura (fig. 6b).
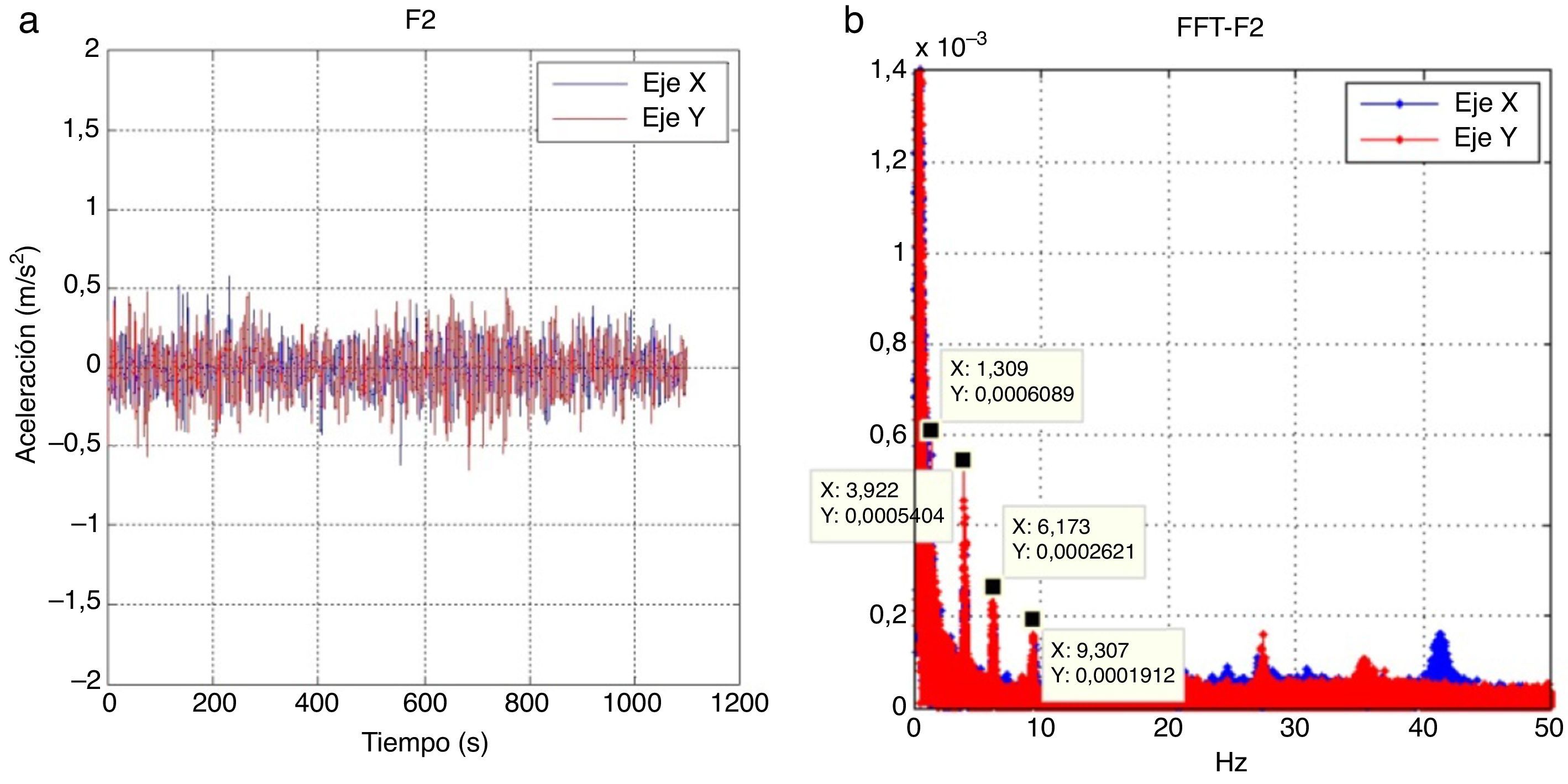
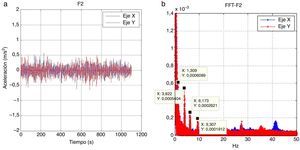
Se realizan diferentes registros de datos con el objetivo de comparar los resultados de cada medición para detectar posibles diferencias aleatorias entre ellos. Las frecuencias de vibración experimentales se obtienen mediante la transformada rápida de Fourier (FFT), que convierte las aceleraciones registradas en el dominio del tiempo al dominio de la frecuencia. Las mediciones se realizan con una frecuencia de muestreo de 100Hz. La elección de esta frecuencia para el procesamiento de datos se establece después de analizar varias mediciones con una frecuencia inicial mayor y tras observar que no hay frecuencias excitadas en la estructura superiores a 50Hz. A modo de ejemplo, la figura 7 muestra las aceleraciones registradas y la FFT correspondiente para el par de puntos de medición (eje X y eje Y) en el forjado F2 durante uno de estos registros de datos. Después de procesar todos los registros de datos, se observa que las 10 primeras frecuencias mostradas en la tabla 3 son similares en la mayoría de las mediciones, por lo que se puede suponer que los 10 primeros modos de vibración de la estructura corresponden a estas frecuencias excitadas.
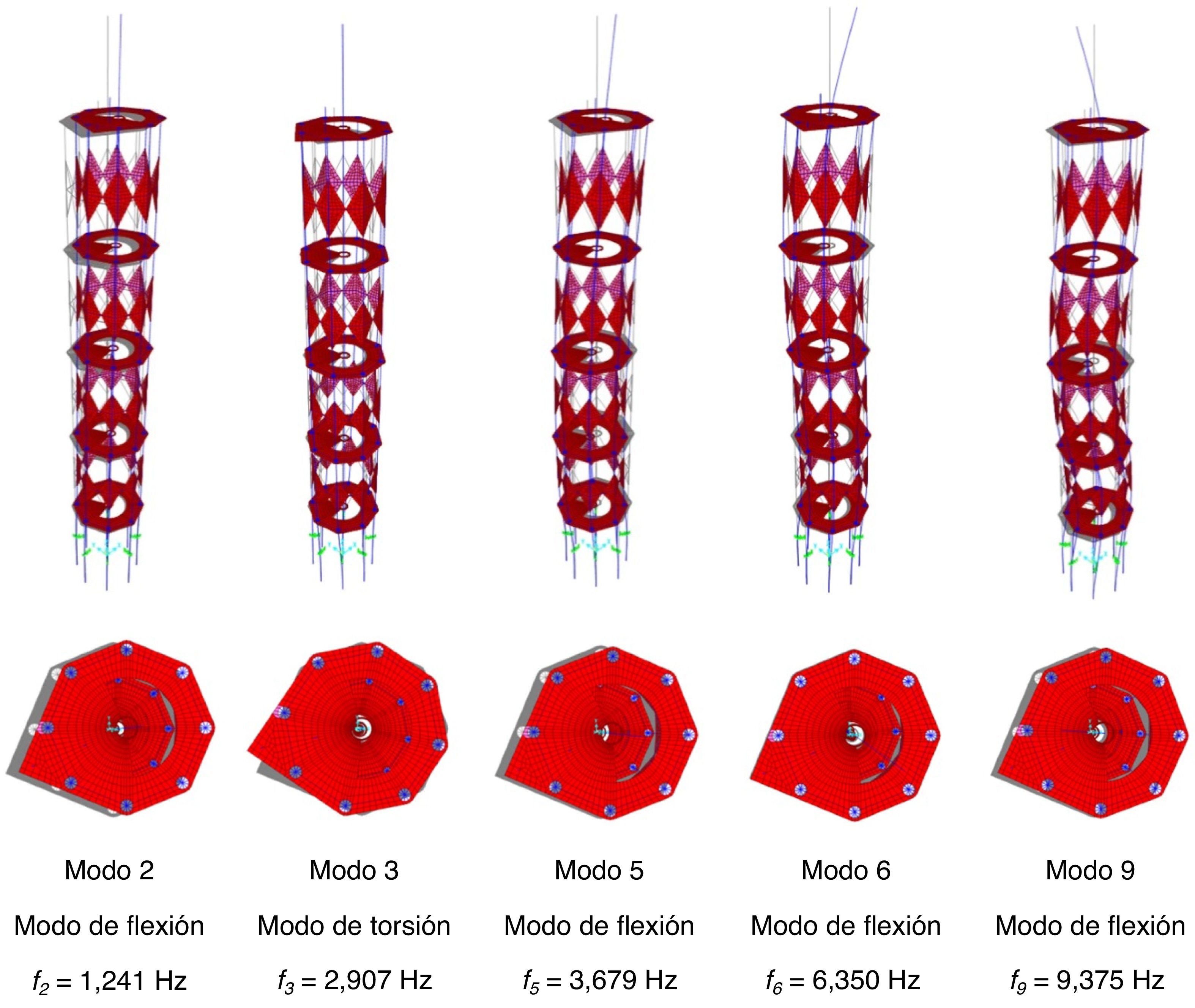
A partir de estos resultados, las primeras 5 formas modales experimentales se pueden comparar con las obtenidas numéricamente. El primer modo de vibración registrado experimentalmente, con una frecuencia de f1,exp=1,309Hz, corresponde al segundo modo de vibración en el análisis numérico, un modo de flexión con una frecuencia de f2,num=1,241Hz. El segundo modo de vibración registrado experimentalmente, con una frecuencia de f2,exp=2,979Hz, corresponde al tercer modo de vibración en el análisis numérico, un modo de torsión con una frecuencia de f3,num=2,907Hz. Los modos de vibración tercero, cuarto y quinto registrados experimentalmente, con una frecuencia de f3,exp=3,922Hz, f4,exp=6,173Hz y f5,exp=9,307Hz, respectivamente, corresponden al quinto, sexto y noveno modos de vibración en el análisis numérico, correspondientes a modos de flexión con frecuencias de f5,num=3,679Hz, f6,num=6,350Hz y f9,num=9,375Hz, respectivamente. En la figura 8 se presentan los modos de vibración en el modelo numérico con frecuencias similares a las de los 5 primeros modos obtenidos experimentalmente, y se comparan en la tabla 4.
El análisis experimental realizado basado en las medidas de aceleración ha demostrado ser una buena técnica para obtener información útil sobre el comportamiento estructural del faro a partir de la vibración libre de la estructura.
El análisis de las aceleraciones inducidas por el viento mediante el uso de la FFT permite identificar los 5 primeros modos de vibración de la estructura, siendo las correspondientes frecuencias experimentales de 1,309; 2,979; 3,922; 6,173 y 9,307Hz. El análisis de las frecuencias se completa con un modelo de elementos finitos, en el que se obtienen frecuencias que solo difieren entre un 1 y un 7% de las obtenidas experimentalmente. Este modelo numérico permite identificar las formas modales experimentales, donde el primer modo corresponde al primer modo de flexión y el segundo al primer modo de torsión, siendo los modos siguientes el segundo, el tercero y el cuarto modo de flexión, respectivamente.
En este caso, en el que los elementos resistentes a flexión (columnas de PRF de carbono) son elementos esbeltos (ratio de esbeltez L/d=24), se puede considerar que para un análisis estructural global resulta suficientemente preciso el uso de leyes constitutivas elásticas lineales de materiales isótropos para los elementos finitos tipo barra (columnas de PRF de carbono, tubos de PRF de vidrio y columna de núcleo central), ya que se comprueba que el valor del módulo de cortante G de los tubos de PRF de carbono apenas afecta al comportamiento dinámico del faro.
El uso de los PRF en la construcción de estructuras singulares en ambientes agresivos es una técnica prometedora que ha sido validada a través de numerosos proyectos en todo el mundo, como por ejemplo el faro presentado en este trabajo. Esta estructura ha cumplido con los requisitos de calidad y estructurales impuestos a este tipo de proyectos, no solo por su comportamiento estático, sino también por su respuesta dinámica.
Los autores desean expresar su agradecimiento a los técnicos de laboratorio e ingenieros del Centro Tecnológico de ACCIONA Construcción en Madrid involucrados en este proyecto, por su participación en el diseño, fabricación y ensayo de la estructura.
Cabe destacar que esta estructura ha sido galardonada con un premio en los JEC World 2016 Innovation Awards en París en la categoría de Infraestructuras con el título «All-composite lighthouse marine navigation aid».