CuNiZn ferrites are polycrystalline ceramic materials that are used widely in electronic devices for a number of reasons, including their high permeability in the RF frequency region, electrical resistivity, mechanical hardness and chemical stability. One of their main applications is in the production of specimens to prevent possible interferences between electronic devices, thanks to their ability to absorb electromagnetic waves. However, their electromagnetic properties are not solely dependent on their chemical composition, but also on the microstructure of the final piece (relative density or total porosity, grain size distribution, pore size distribution, the nature of the grain boundary, presence of secondary phases, dopants, etc.) and, therefore, on the morphology and size of the starting particles, and the processing method.
The microstructure of the sintered specimens was designed in such a way as to optimize the electromagnetic properties of this ferrite. The solid-state sintering stage was also modeled with this optimization in mind. This sintering model enabled to propose the material transport mechanisms that controlled the densification and grain-growth rates, as well as the relative rates of these two simultaneous processes. The established relationships facilitate the design of a thermal cycle suitable for the manufacture of ferrite pieces with maximum relative density and the necessary microstructure. Together with the pre-configured chemical composition, the idea is that this ensures a strong set of final electromagnetic properties.
The electromagnetic properties of the sintered ferrites were observed to improve as sintered relative density and average grain size increased, provided there was no evidence of exaggerated grain growth. In this sense, it seems there is a threshold of the grain size as of which the electromagnetic properties of the sintered specimens get worse. A linear relationship was observed between the imaginary part of the complex magnetic permeability and average grain size, provided each of the different magnetization mechanisms contributing to the complex permeability of the ferrite are taken into account (i.e. spin rotation and wall motion mechanisms).
Las ferritas de CuNiZn son materiales cerámicos policristalinos ampliamente utilizados en dispositivos electrónicos debido a su elevada permeabilidad en la región de RF, resistividad eléctrica, resistencia mecánica y estabilidad química. Una de sus principales aplicaciones es la obtención de piezas para la prevención de posibles interferencias entre aparatos eléctricos debido a su capacidad de absorción de la radiación electromagnética. Pero estas propiedades electromagnéticas no solo dependen de su composición química, sino también de la microestructura del producto final (densidad relativa o porosidad total, distribución de tamaños de grano, presencia de fases secundarias, dopantes, etc.) y, por lo tanto, de la morfología y el tamaño de las partículas de partida y del método de procesado.
Con el fin de optimizar las propiedades electromagnéticas de este tipo de ferritas se ha diseñado la microestructura de las piezas sinterizadas. Para ello, se ha modelizado la etapa de sinterización en estado sólido. Este modelo de sinterización ha permitido proponer los mecanismos de transferencia de materia que controlan las velocidades a las que transcurren los procesos de densificación y crecimiento de grano, así como las velocidades relativas de estos procesos simultáneos. Dichas relaciones permiten el diseño del ciclo térmico más apropiado para la obtención de piezas de ferrita de máxima densidad relativa y microestructura adecuada que, juntamente con la composición química prefijada, aseguren unas buenas propiedades electromagnéticas del producto final.
Se ha observado que las propiedades electromagnéticas de las ferritas sinterizadas mejoran con el aumento de la densidad relativa en cocido y con el tamaño medio de grano, mientras no se produzca un crecimiento exagerado o heterogéneo del mismo. En este sentido, parece que existe un tamaño de grano límite a partir del cual empeoran las propiedades electromagnéticas de las piezas sinterizadas. Asimismo, la parte imaginaria de la permeabilidad magnética compleja varía linealmente con el tamaño medio de grano, siempre y cuando se tenga en cuenta cada uno de los mecanismos de magnetización que contribuyen a esta propiedad electromagnética (rotación de spin y desplazamiento de paredes de dominio).
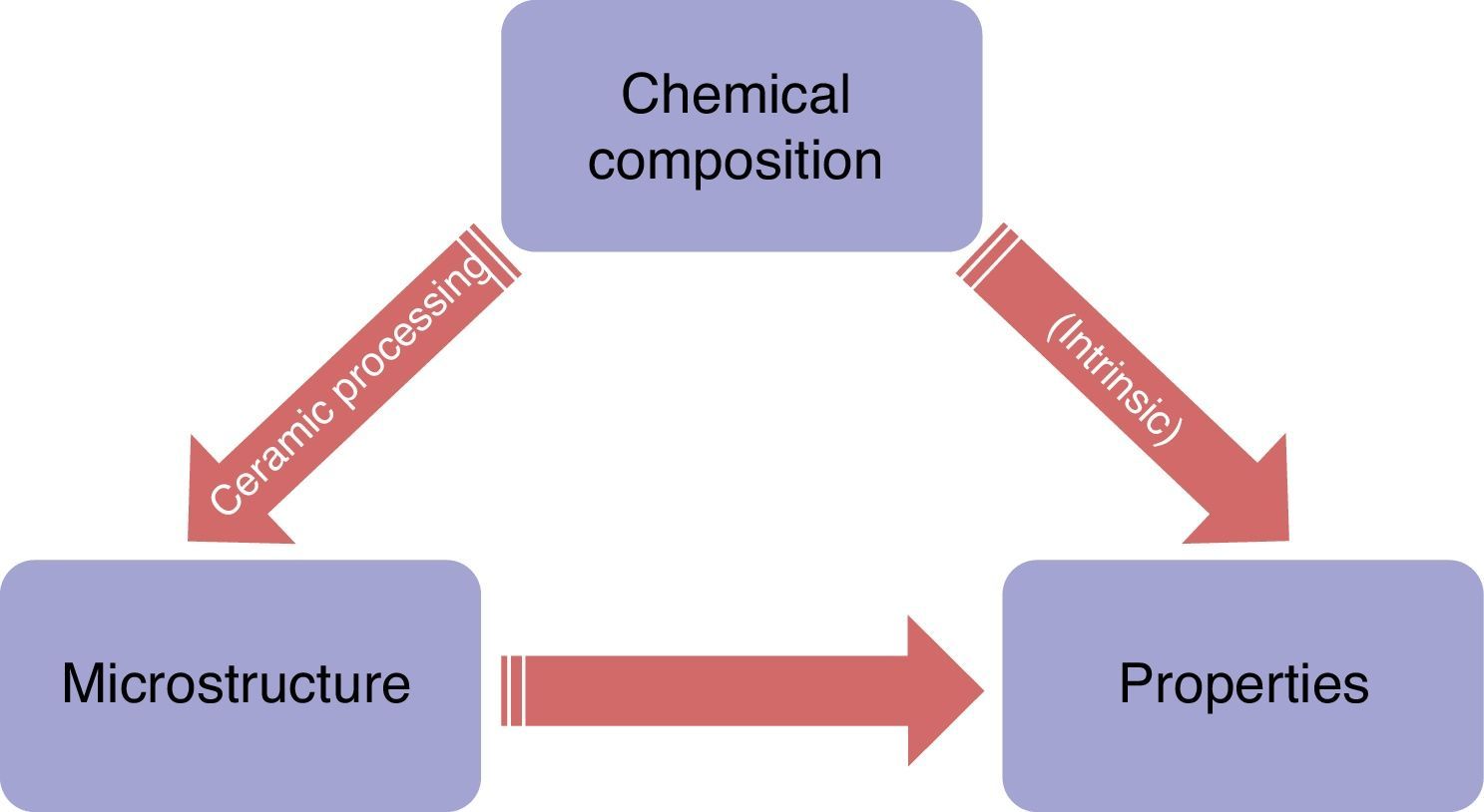
In the manufacture of ceramics products, chemical composition and microstructure are specified with a view to optimizing the mechanical, electric, dielectric, optical, thermal, physical and or magnetic properties of the finished product for a specific application. These optimum properties are achieved by defining, controlling and developing processes that result in the desired microstructure. In this process, the processing technique, microstructure and properties are all interrelated, with changes in one inseparably linked to changes in the others [1]. It is therefore essential to understand these relationships in order to manufacture a high-quality reliable product (see Fig. 1).
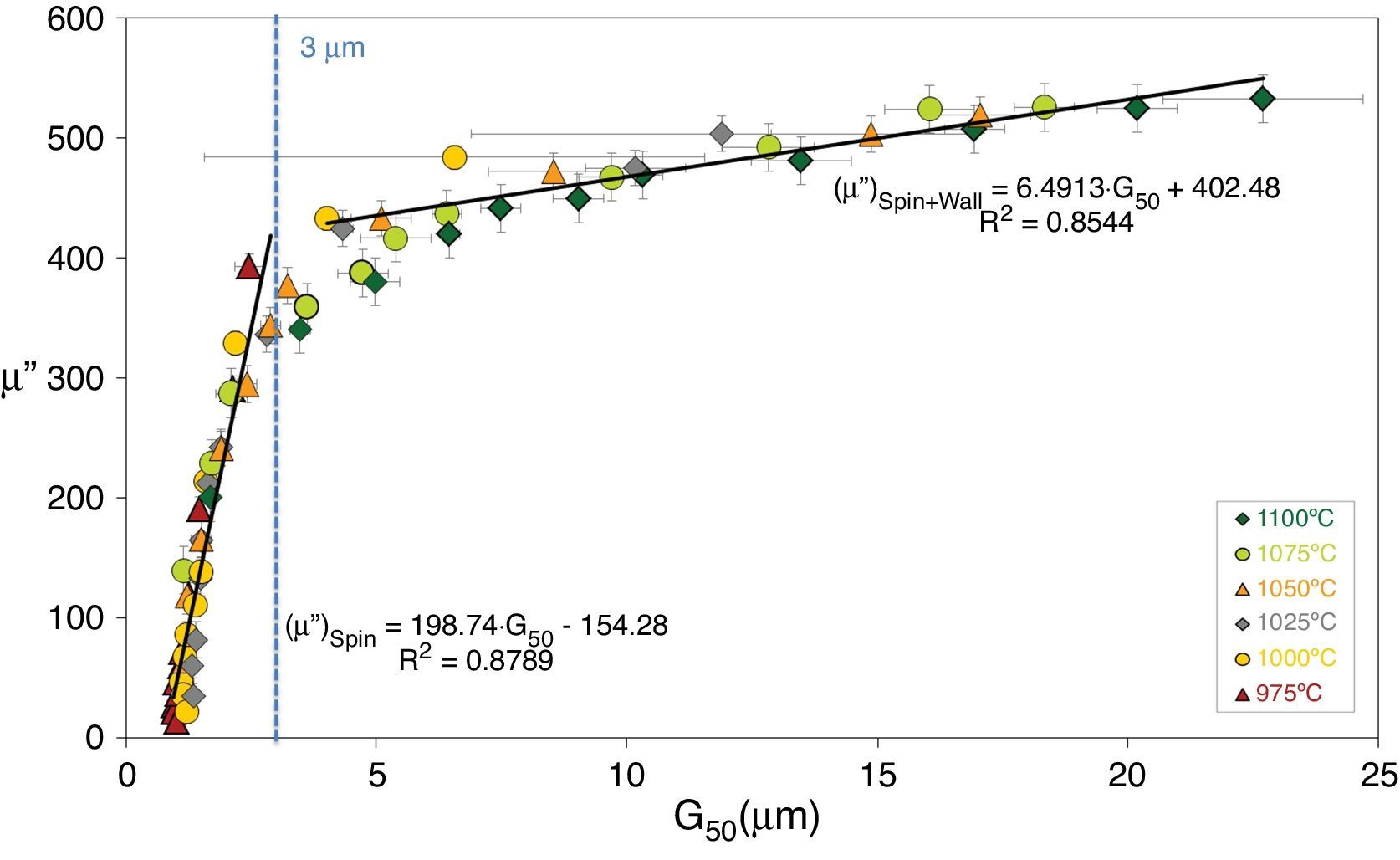
The ceramics consolidation process includes green body forming, pre-sinter thermal processing and a sintering stage. Badly selected green and sintering process parameters will give the final bulk material poor properties [2,3]. Studies have shown how the electromagnetic properties of CuNiZn ferrites worsen significantly in the event of exaggerated and/or abnormal grain growth. The imaginary part-μ″ of the complex permeability of the sintered ferrites has been observed to improve with sintered relative density and average grain size (G50). Additionally, a linear relationship has been found between μ″ and G50 (see Fig. 2), provided each of the different magnetization mechanisms contributing to the complex permeability of the ferrite are taken into account (spin rotation and wall motion mechanisms) and there is no evidence of exaggerated grain growth [4,5].
Maximum imaginary part of the complex permeability (μ″) as a function of average grain size (G50), taking into account each of the different magnetization mechanisms that contribute to the complex permeability of the ferrite (spin rotation and domain wall motion) [4].
During this consolidation process, a variety of chemical and physical changes can occur, including pore shrinkage and elimination, densification, grain growth, secondary phases precipitation, etc. [1,6]. This means it is not only necessary to select the right chemical composition in order to get the desired properties [7], but also to control and ensure that this chemical composition is not altered during the ceramic processing. For instance, in previous studies by the current authors [8,9] it was found that, during the sintering process of a CuNiZn ferrite, the precipitation of zinc oxide (ZnO) and copper oxide (CuO and Cu2O) crystals occurred when the densification and grain growth stages were developed with an oxygen deficiency (see Fig. 3). The occurrence of these crystal precipitates was found to vary in response to the microstructure of the unfired specimens (green microstructure) and the sintering parameters (temperature and time).
Cross-sectional SEM micrograph showing the microstructure and grain boundaries of a sintered specimen with zinc oxide and copper oxide(s) crystal precipitates [8].
Processing-microstructure, microstructure–property, and processing–property relationships can be identified, monitored and controlled through the characterization of the ceramic body during the various stages of processing and after thermal consolidation. By understanding processing–microstructure–property relationship it is possible to modify and optimize the final properties of the bulk material. An understanding of these relationships also allows the identification and correction of processing deficiencies when the desired properties are not achieved.
This paper is focused on the microstructural design of a sintered CuNiZn ferrite specimen, keeping constant the chemical composition of the material and the microstructural target (relative density close to the theoretical one, and small and narrow grain size distribution).
Technical ceramics like the ceramic ferrite materials being studied here should be sintered to almost theoretical density (zero porosity) in order to ensure that the intrinsic properties of the selected material remain invariable in the final bulk specimen. In the same vein, the final average grain size should be relatively small (≈15μm) with a narrow grain size distribution, i.e. exaggerated and heterogeneous grain growth should be avoided.
A densely sintered (low porosity) microstructure (≥0.95, 95% of the theoretical density) is required to elicit a good electromagnetic performance from the sintered ferrite specimens, given that any pores obstruct the wall motion of the domains, thereby reducing the demagnetization field [10,11]. However, it is very important that the specimen's residual porosity is not trapped within the grains (something which is generally associated with the growth of large grains), because this trapped porosity hinders the magnetization process, resulting in lower permeability [12]. That said, it is not only trapped pores that can worsen the electromagnetic properties of polycrystalline ferrites, but also the grain boundaries: these normally act as impurity sinks, concentrating structural disorders and defects, in particular precipitated non-magnetic phases, which can impede the rotation of spins and the motion of the domain walls, thereby decreasing the specimen's initial effective permeability [4].
Process and parameter selectionThe ceramic powders must be consolidated into a bulk body with the microstructure required for the final application. The two requirements can be met by carefully controlling two main processing steps: green processing and sintering. These steps are quite closely intertwined, meaning that the characteristics of the powder will strongly affect the quality of the product after sintering. A coordinated process is therefore necessary in which the green processing and sintering enhance each other [13].
The processing–microstructure relationship is influenced by the morphology and particle size distribution of the raw materials, green processing and sintering stage. The selection of the processing route and parameters at each stage will determine the final microstructure of the bulk ceramic material and, with it, its final properties.
Green processingThe ceramic fabrication technique selected will depend on the nature of the ceramic material (glass, particulate forming or cement) and the geometry requirements of the final product (fiber, film, bulk, etc.). As previously stated, these CuNiZn ferrites are manufactured by the denominated conventional ceramic process, which comprises raw materials preparation, synthesis (if needed), milling, agglomerating and compaction stage [14–16].
When selecting which raw materials to use to synthesize the powder (usually, metallic oxides), there are different factors that should be evaluated: impurity level, reactivity (particle size), powder processing method and cost [17]. If high-quality bulk materials are needed [3], purity should be set very high (less than 0.1% total impurities). The required particle size of the raw materials depends on the equipment being used in processing. For instance, dry blending without milling will require finer particle sizes than a wet ball milling process. The reactivity of the raw materials is an operational parameter that is well-understood but difficult to measure quantitatively because it depends on multiple properties of the powder, including particle size, specific surface area and particle geometry [13].
In contrast to the chemical methods [18–21], which produce high-quality powder materials, the traditional ceramic method facilitates the processing of raw materials on an industrial scale [17,21], which is why it is the method preferred by ferrite manufacturers. During synthesis (or calcining), which is generally conducted 100–300°C below sintering temperature, the formation of the powder's lattice begins with the interdiffusion of the substituent oxides into a chemically- and crystallographically-uniform structure. When the raw materials mixture is not heat-treated, a reactive sintering will be carried out afterwards. In this case, the sintering process is a combination of two isolated processes: reaction and densification. A balance between the densification and reaction rates is required in order to achieve densification before the reaction interferes with the densification process [22]. The shrinkage of the final piece during the sintering process is lesser when starting from the synthesized powder than from the metallic oxides mixture, and the homogenization of the material is improved [13].
The milling, typically by wet method, is carried out in iron carbon-less mills. The equipment and mill media materials, processing times and speeds should be selected appropriately. At this stage, the parameters being controlled are average particle size and particle size distribution width, which determine the homogeneity of the compacted powder going into the final firing, as well as the microstructure of the specimen after the sintering process [13].
After milling, the powder suspension (or slurry) must be converted to compacted powder. Spray drying is the most general agglomeration process used for this and the main variables that need to be configured include nozzle diameter, feeding rate and temperature. To ensure a good dispersion of the powder on the wet agent, to enable this stage and to achieve the desired behavior of the powder during the next stages (agglomeration and compaction), it is imperative that the additive system (dispersant, binder, plasticizer, lubricant, antifoaming, etc.) be carefully selected. At this stage, granule size distribution is normally selected as the main control parameter, and will determine the fluidity of the powder and the appropriate fill of the pressing die.
The final stage, compaction, is mainly carried out by die-press, in which the maximum pressure value is the main variable that needs to be set and controlled. Simple shapes such as toroids or E cores are pressed with single-level lower punches, while more complicated shapes like pot cores are compacted with secondary lower punches [13]. Die-pressing produces specimens whose density gradients may be the result of the friction of the powder moving along the die-wall. To reduce this problem, external lubricants such as zinc-stearate may be used. In order to control the process, green relative density (porosity) and pore size distribution are tested in the green bulk specimens.
SinteringThe sintering process is closely tied to the characteristics and properties of the powder, and to the powder processing method (green processing) [23]. The purposes of the sintering process are: (i) to complete the interdiffusion of the component metal ions into the desired crystal lattice, if reaction has not been previously completed; (ii) to establish the appropriate valencies for the multi-valent ions by proper oxygen control, and; (iii) to develop the most appropriate microstructure for the application [13]. The implications for the latter are (iii.a) obtaining bodies with high relative density (very low porosity); (iii.b) increasing grain size uniformly while maintaining a small average grain size and narrow grain size distribution, and; (iii.c) avoiding abnormal grain growth [24].
In the case of these polycrystalline materials, the two main variables controlling the sintering stage are peak sintering temperature and dwell time at peak temperature. Other variables that should be studied are the heating and cooling rates, and the sintering atmosphere.
In order to get high relative densities with small and narrow grain size distributions (the control parameters at this stage), it is imperative to promote densification over grain growth. An extremely high sintering temperature may promote the decomposition of the spinel structure, causing composition gradients in the material and increasing its final porosity [17]. Similarly, an excessively-high sintering temperature promotes grain growth over densification, leading to the exaggerated and heterogeneous growth of the grains. The growth of large grains leads to many pores being swept over by the grain boundary, remaining within the large grains [25]. From an electromagnetic point-of-view, intragranular porosity is more deleterious than the intergranular, worsening the final properties of the bulk ceramic material.
In addition to the known thermal treatment variables (temperature, time, heating/cooling rate and atmosphere), other parameters affect the development of the sintering process, such as secondary particles, dopants, impurities and even porosity itself [26].
From a microstructural point-of-view, the main goal of sintering is to achieve a reproducible final microstructure, which was previously designed. This requires an exhaustive microstructural control, including over sintered bulk density (total porosity), and grain and pore size distribution, with particular emphasis on the average grain and pore sizes.
Two simultaneous processes take place during the sintering process: densification and grain growth. There are three ways of enhancing the densification process of a material: (i) by increasing sintering temperature; (ii) by decreasing the mean particle size of the raw materials (making the raw materials more reactive); and (iii) by means of a pressure-assisted sintering [25,27]. However, it is physically impossible to increase the relative density of a specimen without also promoting grain growth in the particles [28].
The sintering process can be divided in three stages: (i) the initial stage, from green relative density to 2–3% porosity reduction at most, which is characterized by particle adhesion and the formation of necks between particles; (ii) the intermediate stage, up to 93% of relative density, where the porosity of the specimen is still interconnected, and; (iii) the final stage, corresponding to the last 7% of residual porosity (close to the theoretical density), which is typified by the isolation of the remaining pores. This kind of technical ceramic requires processing up to the final stage in order to get a high-density body while inhibiting, as far as possible, the grain growth process as the dominant sintering process [25].
In the grain growth process, the pore drag rate must be similar to the grain growth rate for the pores to move jointly with the grain boundaries. If the pore drag rate were smaller than the grain boundary advance rate, the pores would remain trapped inside the grain, making it impossible to eliminate them by conventional thermal treatment, and thus reducing the final attainable relative density [29–32].
As mentioned, grain growth is an unavoidable process (based on Ostwald ripening mechanism [33,34]), but it can be controlled by different methods: (i) the addition of secondary particles (physical Zener effect [35]) and/or chemical dopants (chemical effect) [36], which act on the grain boundary mobility [26]; (ii) the porosity itself, which acts as a control method with the dual effect of the grain boundary mobility and pore mobility, and; (iii) the design of an appropriate thermal cycle to promote densification over grain growth.
At this point, it seems clear that the selected thermal treatment will determine the final microstructure of the ceramic material, and that in order to reach a relative density that is close enough to the theoretical density, it is imperative to promote densification and inhibit the grain growth process. For this latter, and when actions causing alterations to chemical composition are forbidden, the design of a suitable thermal cycle seems to be the better option. Some difficulties that must be overcome include the large number of variables that must be studied and the fact that the available theoretical models are non-predictive models that only allow a posteriori qualitative explanation of the experimental data.
To this end, it is proposed to use a mathematical solid-state sintering model based on the physical phenomena that take place during the sintering stage, in order to establish the material transport mechanisms controlling the densification and grain growth rates and the relative rates of these two simultaneous processes. This referred information will enable the design of an appropriate thermal cycle for the manufacturing of bulk ceramic pieces of maximum relative density and suitable microstructure, which together with the pre-set chemical composition will ensure that the pre-established final properties are correctly achieved.
Two general equations of densification and pore-dragged normal grain growth rate during the final stage of sintering are proposed in the literature [25,37–39], for use in determining the microstructural development of the sintered ferrite specimens. If relative density (ϕ) and adimensional average grain size (η) are included, these equations can be written as follows:
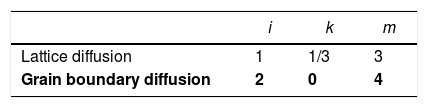
where K1i and K2i are complex temperature functions that comprises constant parameters (such as the volume of material moved in association with one ion of rate-controlling species, the Boltzmann constant, average starting particle diameter, etc.), temperature-dependent parameters (such as the number of pores per grain, the diffusion coefficients for both processes, the solid/gas surface energy, etc.), and temperature itself. Consequently, K1i and K2i must be constant at each temperature and green microstructure, where ‘1’ refers to the densification process, ‘2’ to the grain growth process, and ‘i’ depends on the material transport mechanisms controlling each of these processes (see Tables 1 and 2). In the same way, k, m, ℓ and n are exponents that depend on the controlling mechanism, as also set in Tables 1 and 2.Material transport mechanisms controlling the grain-growth rate in the sintering model. Marked values correspond to the result found for the case study of the CuNiZn ferrite.
| i | ℓ | n | |
|---|---|---|---|
| Pore drag control | |||
| Surface diffusion | 1 | 4/3 | 4 |
| Lattice diffusion | 2 | 1 | 3 |
| Gas phase diffusion | 3 | 1 | 3 |
| Evaporation/condensation | 4 | 2/3 | 2 |
| Boundary mobility control | 5 | 0 | 2 |
As K1i and K2i are unknown complex functions of temperature and green microstructure (in the compaction process used in this study, they directly depend on pressure – P), empirical relationships of the following form can be proposed:
Another useful equation that can be used is the rate ratio (Γ), defined as the quotient of densification rate (dϕ/dt) to grain growth rate (dη/dt) as follows:
which enables an expression of ϕ=f(η) to be obtained by separating variables and integrating analytically. If m≠n, Eq. (6) could be written as follows:and if m=n, as follows:A case study: process design for a CuNiZn ferriteGreen processingKeeping a constant weight formula, and a constant particle size distribution and particle morphology and characteristics of the raw materials will ensure the invariance of the first stages of the green processing, but it will not ensure the invariance of the material's chemical composition. As previously mentioned, the processing not only alters the microstructure of the final piece (and therefore the final properties) [4,5], but it also can disrupt its chemical composition when, for example, a precipitation of a secondary phase is produced during the sintering stage [8,9]. However, this can be avoiding through accurate control of the sintering parameters.
The green processing of the CuNiZn ferrite was set as follows. The powder of the chemical composition (Cu0.12Ni0.23Zn0.65)Fe2O4 was wet ball milled to an average particle size of 2μm and narrow particle size distribution (around 4μm), as shown in Fig. 4(a). The milled powder was put into a water suspension using an ammonium polymethacrylate as dispersant agent, a polyvinyl alcohol as binder and a polyethylene glycol as plasticizer in a suitable proportion, and spray dried to produce spherical granules with high flowability (average granule size of 175μm). See Fig. 4(b). The granules were used to form cylindrical test specimens by uniaxial pressing at a green relative density of around 60% and via a four-stage pressing cycle with three de-airing stages and one forming stage at maximum pressure (200MPa). Zinc stearate was used as lubricant agent.
In order to achieve the required final sintered microstructure (high relative density, and a small and narrow grain size distribution) it is imperative to use raw materials with a small and narrow particle size distribution. This requirement entails a bad compaction of the green specimen, making it vital to use high pressures at the compaction stage in order to get a reasonably high green relative density, in order to enable the manufacture of a final ceramic piece with a relative density close to the theoretical density (close to zero porosity).
SinteringThe experimental data needed for the physical-mathematical modeling and the design of the thermal cycle were the relative density (ϕ) and adimensional average grain size (η) of the ferrite specimens compacted at different pressures (P), sintered at different temperatures (T) and with different dwell times (t). The specimens were pressed at six pressures (50–300MPa), sintered in air in an electric laboratory kiln at ten peak sintering temperatures (900–1200°C) and eleven dwell times (0–30h), using a three-stage thermal cycle described in previous papers [40,41]. The methods used to determine the relative density (ϕ) and the adimensional average grain size (η) of the sintered specimens are also described in the aforementioned previous papers [40,41].
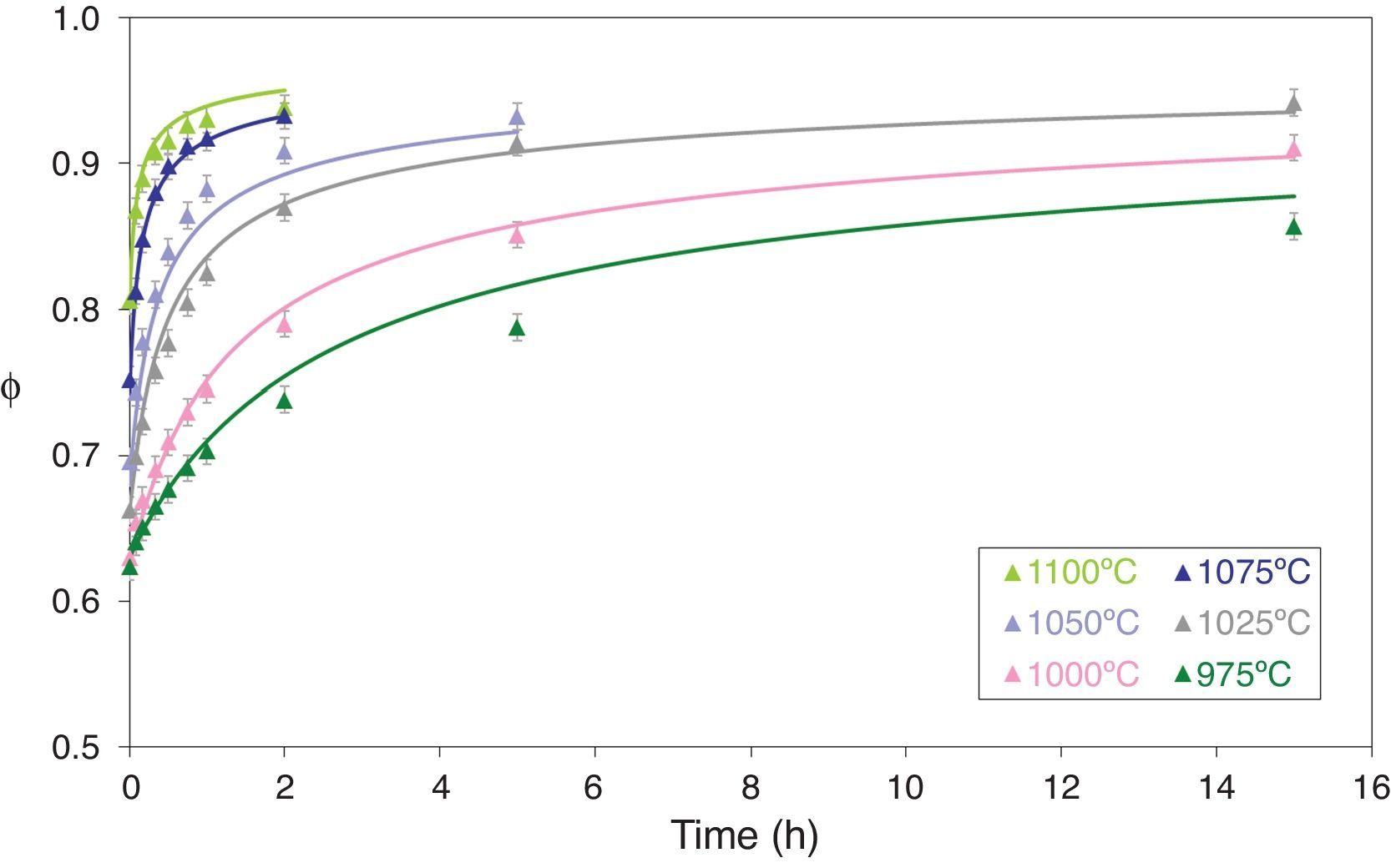
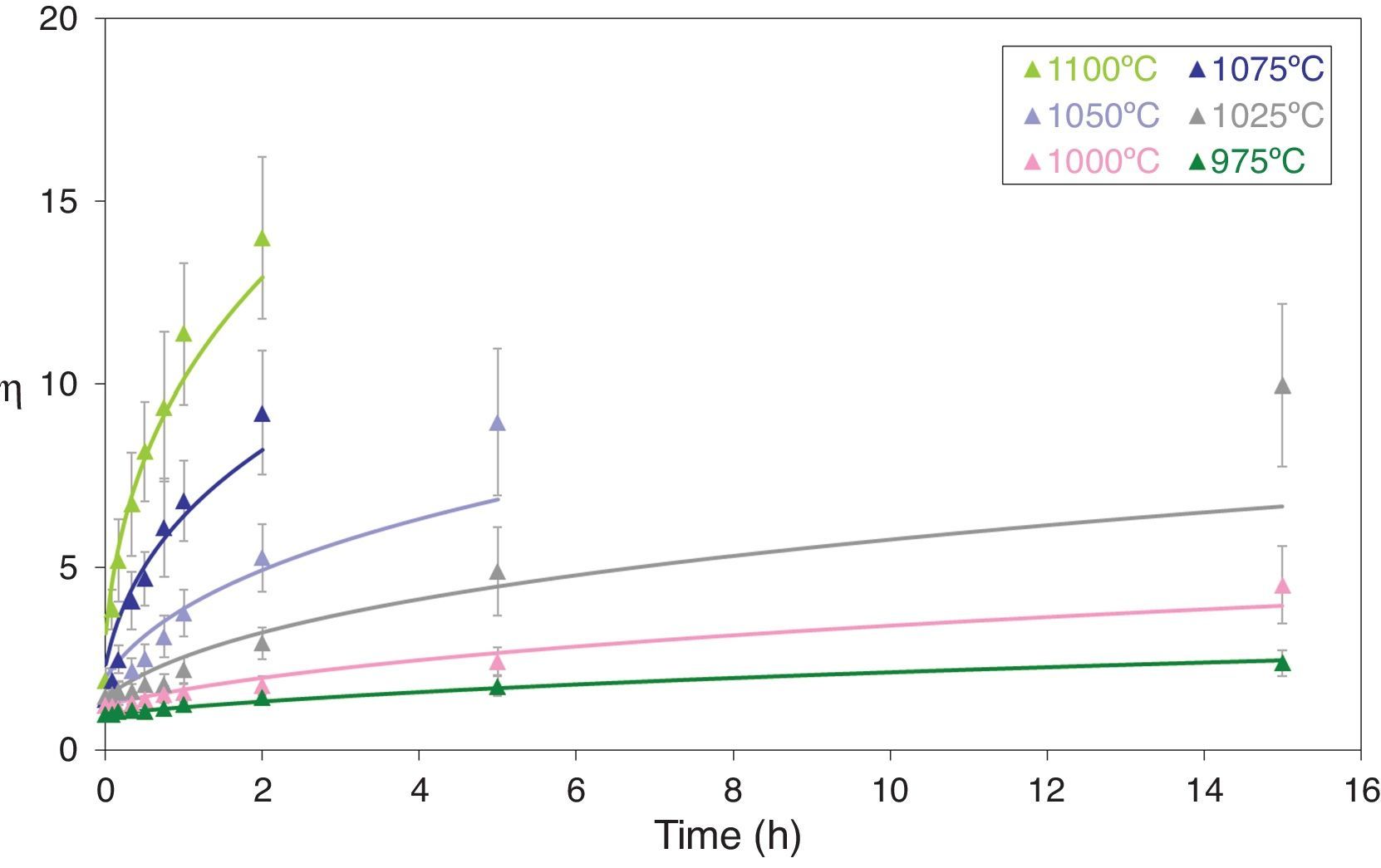
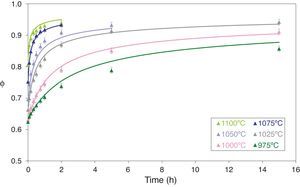
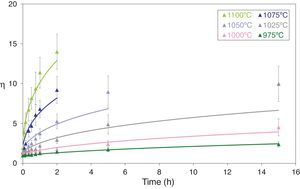
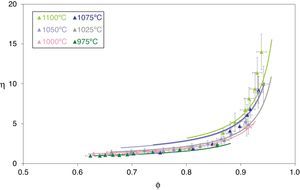
Figs. 5 and 6 depict the evolution of the relative density and adimensional average grain size of the studied specimens (fired at sintering temperatures of 975°C, 1000°C, 1025°C, 1050°C, 1075°C and 1100°C) with sintering time (zero sintering time corresponds to the attainment of the uniform setting temperature). The dots correspond to the experimental data. The experimental data corresponding to the highest (1150°C and 1200°C) and lowest (900°C and 950°C) sintering temperatures have not been modeled, because the model was proposed for normal grain growth at the final stage of sintering. However, for the mentioned highest temperatures, exaggerated and heterogeneous grain growth was observed, while for the lowest the sintering process seems to be developed at the intermediate and not the final stage.
Relative sintered density (ϕ) as a function of sintering time at 975, 1000, 1025, 1050, 1075 and 1100°C. The discrete points represent the experimental data while the lines correspond to the results obtained by the simultaneous integration of Eqs. (13) and (14).
Adimensional average grain size (η) as a function of sintering time at 975, 1000, 1025, 1050, 1075 and 1100°C. The discrete points represent the experimental data while the lines correspond to the results obtained by the simultaneous integration of Eqs. (13) and (14).
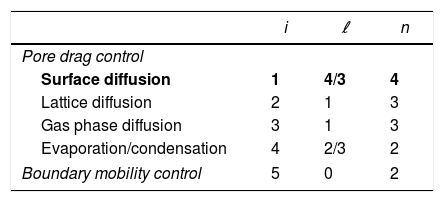
The plot of ln(dϕ/dt)−k·ln(1−ϕ) versus ln(η) yields six straight lines of slope close to −4 (m=4), only when k=0. This value suggests that, during the sintering of the CuNiZn ferrite studied, boundary diffusion appears to be the material transport mechanism that controls the densification rate, not lattice diffusion. In the same way, the plot of ln(dϕ/dt)+ℓ·ln(1−ϕ) versus ln(η), for a value of ℓ=4/3, yields six straight lines of slope close to −3 (n−1=3, or n=4). The data did not fit either the lattice or gas phase diffusion pore drag control model (ℓ=1), the evaporation/condensation diffusion pore drag control model (ℓ=2/3), or the boundary mobility control model (ℓ=0). Therefore, it is reasonable to conclude that under the set conditions grain growth is governed by surface diffusion pore drag control. Therefore, Eqs. (1) and (2), taking into account that K1i=K12 and K2i=K21 (according to Tables 1 and 2), can be rewritten as follows:
Table 3 details the values of the effective diffusion coefficients of the densification (K12) and grain growth rates (K21) for the six studied temperatures at 200MPa. Similar values were obtained for the other five pressure values.
Effective diffusion coefficients of the densification (K12) and grain growth (K21) rates obtained for the different sintering temperatures studied at 200MPa, corresponding to the case study of a CuNiZn ferrite.
| T (°C) | K12 | K21 |
|---|---|---|
| 1100 | 201 | 99.7 |
| 1075 | 55.1 | 20.4 |
| 1050 | 13.3 | 4.15 |
| 1025 | 2.98 | 1.25 |
| 1000 | 0.524 | 0.188 |
If Eqs. (3) and (4) are followed, plotting the values of K12 and K21 (at each pressure value) versus the inverse of temperature on semilogarithmic paper should yield two straight lines (one for each pressure). In effect, the plot of the K12 and K21 values versus the inverse of temperature (according to Arrhenius law) gives two straight lines for each tested pressure (with a coefficient of determination r2 greater than 0.99). Since the exponential and pre-exponential factors of the equations obtained for each pressure has been observed to vary with the green microstructure, it has been possible to get an empirical relationship of these factors (pre-exponential and exponential) with the compaction pressure, also giving a good straight line fit (coefficient of determination r2 greater than 0.99). These correlations between the effective diffusion coefficients and sintering temperature, and the exponential and pre-exponential factors of the Arrhenius equations and compaction pressure yield to the following equations, for all the values of T and P tested:
Therefore, combining Eqs. (9) and (10) with (11) and (12), the densification and grain growth rates of the studied CuNiZn ferrite under the set conditions can be described by the following equations:
Eqs. (13) and (14) can be simultaneously integrated by a numerical method, obtaining the curves showed in Figs. 5 and 6, which show a good correlation between the experimental data (discrete points) and the calculated data, at any pressure and temperature. The graphs shown in Figs. 5 and 6 correspond to the pressure value of 200MPa. Similar figures were obtained for the other pressure values tested.
The relationship between ϕ and η can be obtained from Eq. (8):
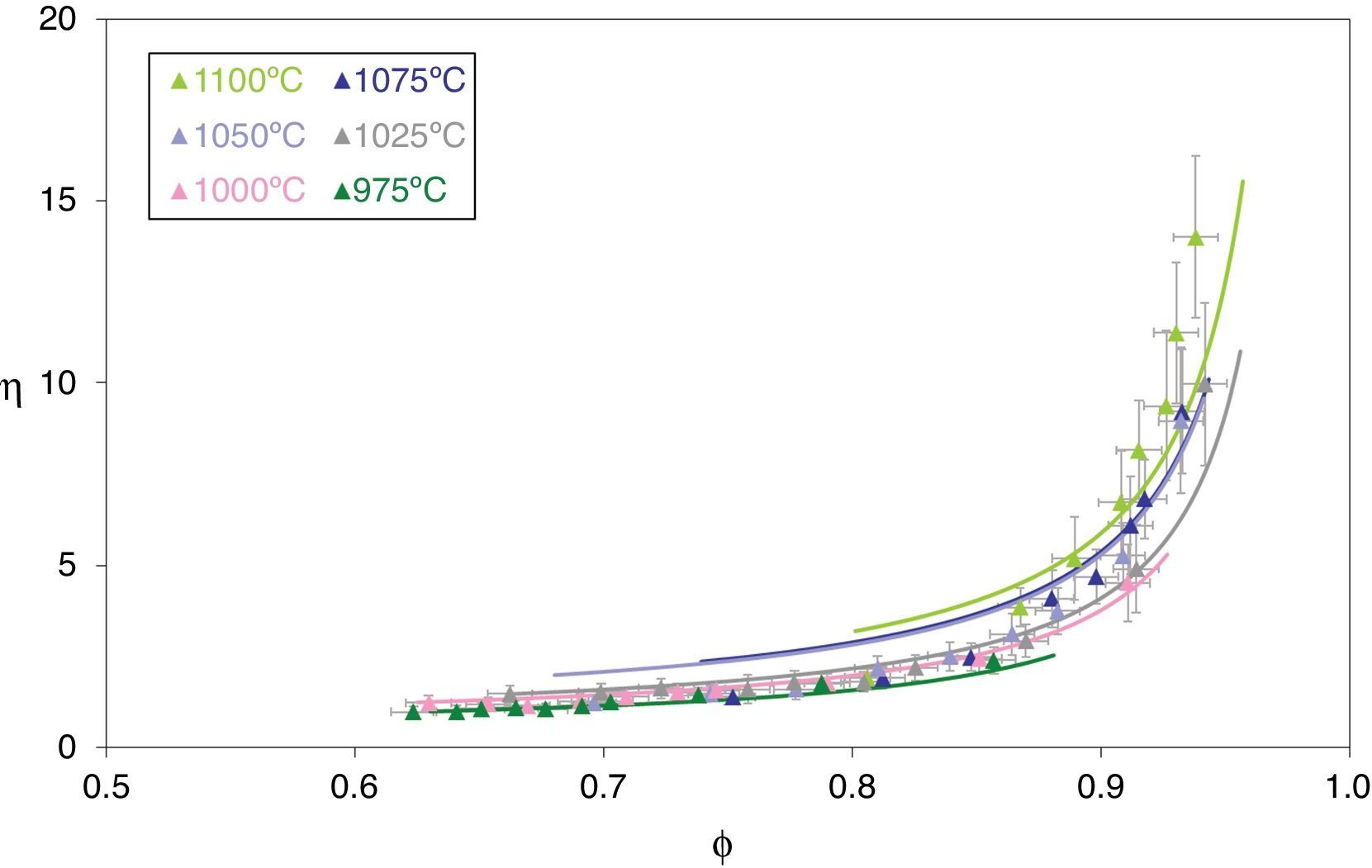
while combining Eqs. (15), (11) and (12) gives:Fig. 7 depicts the adimensional average grain size (η) as a function of relative sintered density (ϕ) at 975°C, 1000°C, 1025°C, 1050°C, 1075°C and 1100°C. The discrete points represent the experimental data while the lines correspond to the results obtained from Eq. (16), which successfully reproduce the experimental results. The results shown in Fig. 7 correspond to the pressure value of 200MPa. Similar figures were obtained for the other pressures studied.
Adimensional average grain size (η) as a function of relative sintered density (ϕ) at 975, 1000, 1025, 1050, 1075 and 1100°C. The discrete points represent the experimental data while the lines correspond to the results obtained by Eq. (16).
Eqs. (13) and (14) suggest that in order to manufacture ferrite specimens with a high sintered relative density, the sintering process should be conducted at the maximum allowable temperature, so as to ensure a high densification That said, if this high sintering temperature is maintained, grain growth rate will also be extremely high, causing exaggerated grain growth. Therefore, a sintering stage conducted at an extremely high and constant sintering temperature is not appropriate, because heterogeneous sintered microstructures will be obtained, thereby worsening the final properties of the material [29–31]. Eqs. (13) and (14) also highlight that, for the conditions studied, the grain growth rate is always higher than the densification rate, representing an additional challenge in the design of the thermal cycle.
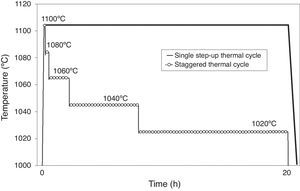
In light of the above, the design of the thermal cycle has been conducted along two basic statements: (i) to conduct the sintering process to the maximum allowed temperature during a certain dwell time, define by the restriction that no exaggerate grain growth can take place, (ii) reached this dwell time, decrease sintering temperature and keep it constant again for another period of time, defined by the same restriction. Decreasing sintering temperature decreases both the densification and grain growth rates, but allows the preservation of the densification process at the highest possible values, controlling the grain growth and preventing an exaggerated and heterogeneous growth of the grains [42,43]. This gradual reduction of the sintering temperature can be carried out as many times as needed, as long as tolerable values are achieved for the densification rate.
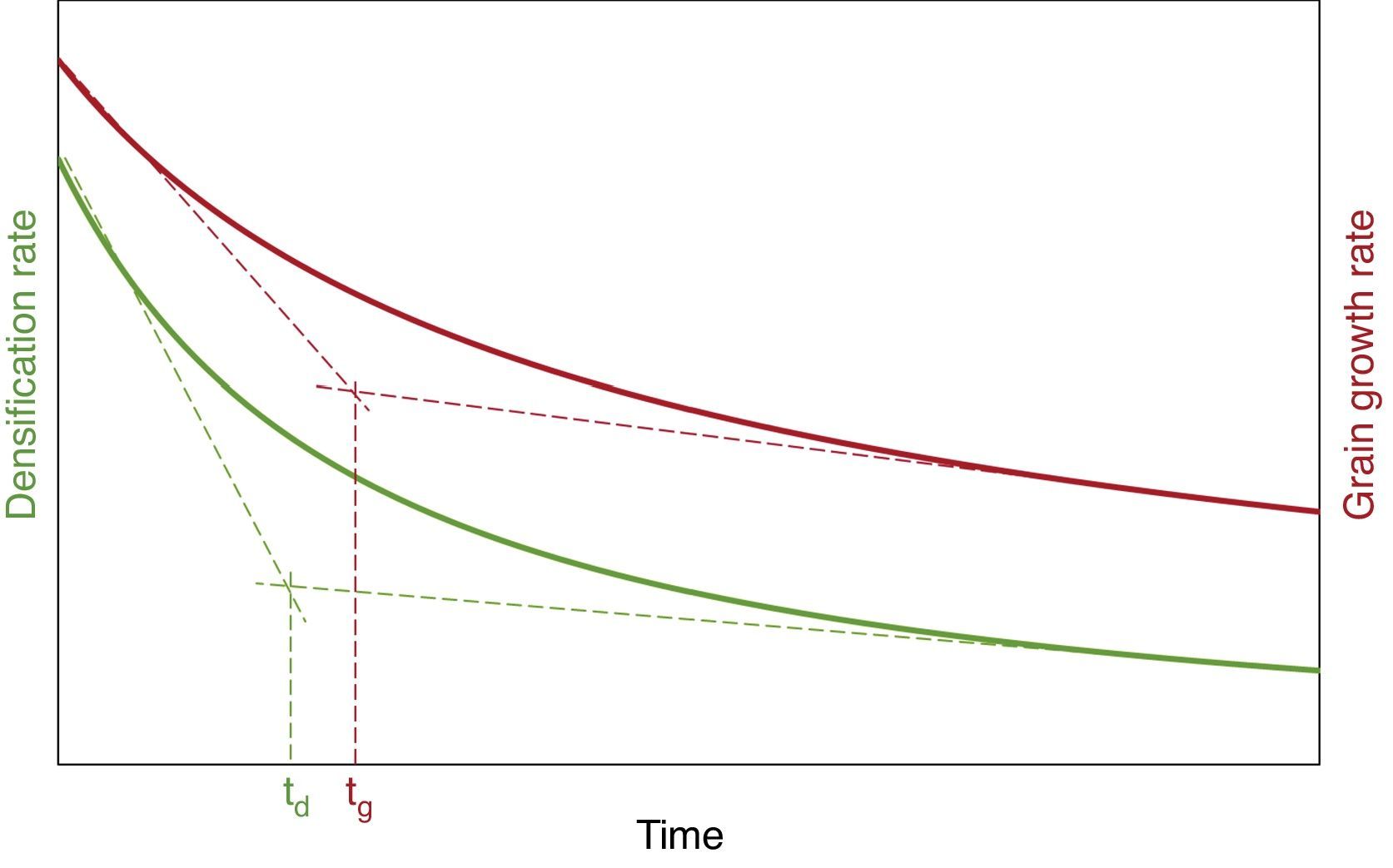
To determine the maximum dwell time at each sintering temperature, the following procedure must be followed: (i) the simultaneous numerical integration of Eqs. (13) and (14) to the aforementioned temperature, obtaining the t, ϕ and η values (evolution of relative density and adimensional grain size with sintering time); (ii) substitution of the t, ϕ and η values in Eqs. (13) and (14) in order to obtain the t, dϕ/dt and dη/dt values (evolution of the densification and grain growth rates with sintering time), obtaining a representation similar to the plot in Fig. 8; (iii) determination of the vertex of each of the rate curves in Fig. 8, calculating them as the intersection of the tangents to the two branches of the rate curves (corresponding to the sintering times of zero and infinite).
Determination of the maximum dwell time at specific sintering temperature [40].
As shown in Fig. 8, two times are obtained: one for the densification rate curve (td) and one for the grain growth rate curve (tg). The lowest time will be chosen as the maximum dwell time at the aforementioned temperature (tmax,T). The selection of this value as tmax,T is due to the fact that: (i) it corresponds to the dwell time at which the densification and grain growth rates stop dropping sharply and start to decrease more slowly (see Fig. 8), an effect that is more pronounced at higher sintering temperatures; (ii) as off this value (as observed in Fig. 8), the differences between the values of the densification and the grain growth rates are larger.
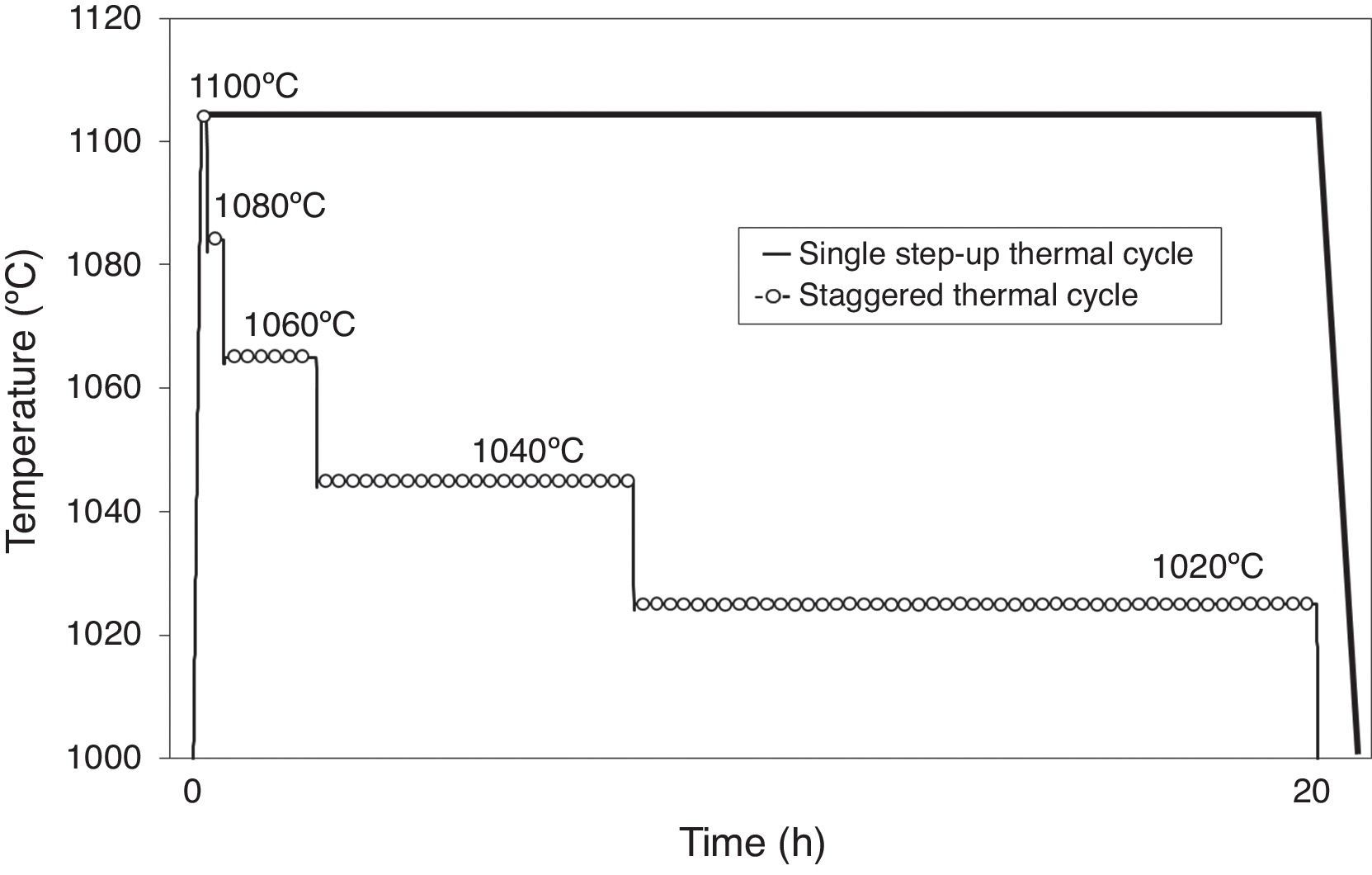
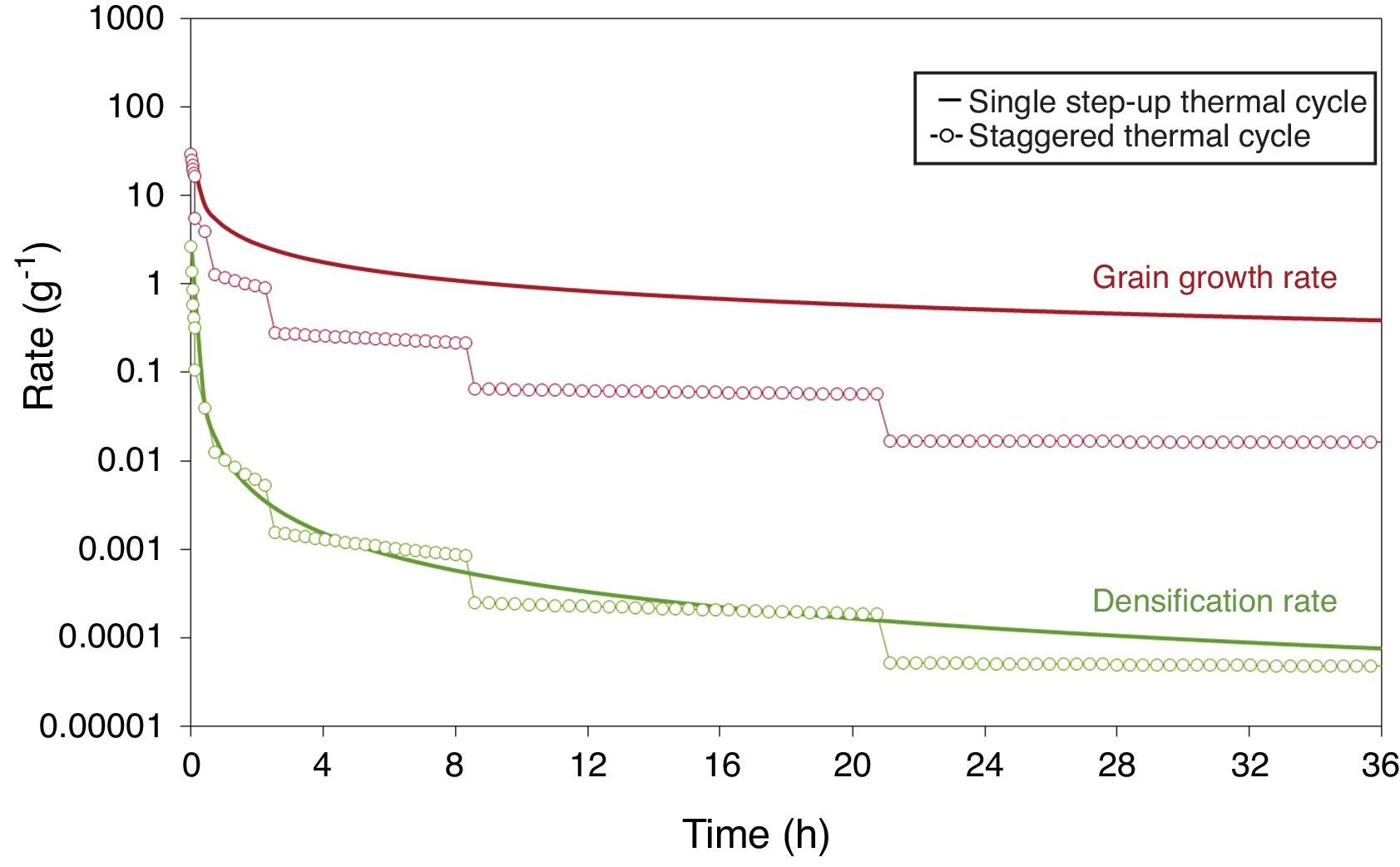
Fig. 9 shows the staggered thermal cycle design the procedure for which is explained above, beginning at 1100°C and slightly scaled down to 1020°C, comparing it to a single step-up thermal cycle at a maximum temperature of 1100°C. Fig. 10 depicts the grain growth and densification rates against sintering time for a single step-up thermal cycle conducted at the maximum sintering temperature of 1100°C, and for the designed staggered thermal cycle shown in Fig. 10. As can be observed, the gradual reduction of the maximum sintering temperature causes a significant reduction of the grain growth rate, but gives almost no change to the densification rate. This should allow the densification of the ferrite specimen to a relative density close to the theoretical value, thereby controlling the grain size growth.
Densification and grain growth rates versus sintering time at 1100°C, comparing a single step-up and a staggered thermal cycle [40].
A green ferrite specimen (relative density of 0.61) was sintered with the designed staggered thermal cycle shown in Fig. 9, leading to a sintered piece with a relative density of 0.96, an average grain size of 11.9μm, and a narrow and homogeneous grain size distribution (20.2μm), following the designed green processing. The sintered microstructure of this CuNiZn ferrite specimen is shown in Fig. 11. The final piece provides good electromagnetic properties, with a maximum value of the imaginary part of the complex magnetic permeability (μ″) of 546, for a frequency of 107Hz.
The following statements can be made based on the analysis of the results from the thermal cycle design: (i) staggering the reduction of the maximum sintering temperature and increasing the dwell time at each temperature increases the sintered relative density up to a value of 0.96, with very controlled grain growth (no bigger than 12μm); (ii) the sintered relative density reaches its highest value at a temperature of 1020°C, so it is not worth decreasing this temperature any further, because is not possible to increase the relative density any more (probably because the densification rate is already down to a minimum), while the average grain size is still increasing and the total sintering stage time drags on unnecessarily.
ConclusionsIn this paper it has been stated how the processing technique employed determines the final properties of ceramics specimens through their microstructural development (green and sintered), and how the pre-set chemical composition must be controlled throughout the whole process, because it can be also altered unintentionally. To achieve the required final properties for the specific application, it is essential to design the final microstructure of the sintered specimen. This can be achieved through the design of the thermal cycle. Specifically, the solid-state sintering stage has been modeled in this study, determining the existing mathematical relationships between the densification and grain growth rates and two processing parameters: sintering temperature and green microstructure (or compaction pressure).
The study has been carried out with funding from the project MAT2016-76320-R, within the scope of the Spanish National Plan for Scientific Research, Development and Technological Innovation of the Spanish Ministry of Economy, Industry and Competitiveness.








![Maximum imaginary part of the complex permeability (μ″) as a function of average grain size (G50), taking into account each of the different magnetization mechanisms that contribute to the complex permeability of the ferrite (spin rotation and domain wall motion) [4]. Maximum imaginary part of the complex permeability (μ″) as a function of average grain size (G50), taking into account each of the different magnetization mechanisms that contribute to the complex permeability of the ferrite (spin rotation and domain wall motion) [4].](https://static.elsevier.es/multimedia/03663175/0000005700000001/v1_201802131616/S036631751730078X/v1_201802131616/en/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Cross-sectional SEM micrograph showing the microstructure and grain boundaries of a sintered specimen with zinc oxide and copper oxide(s) crystal precipitates [8]. Cross-sectional SEM micrograph showing the microstructure and grain boundaries of a sintered specimen with zinc oxide and copper oxide(s) crystal precipitates [8].](https://static.elsevier.es/multimedia/03663175/0000005700000001/v1_201802131616/S036631751730078X/v1_201802131616/en/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
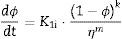
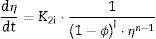
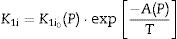
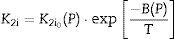
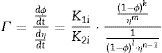
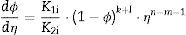
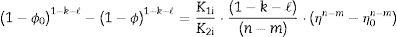
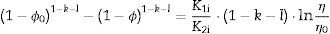

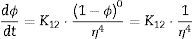
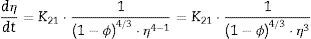
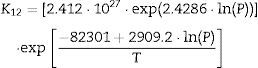
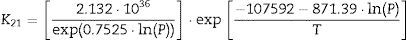
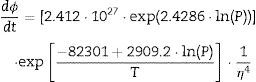
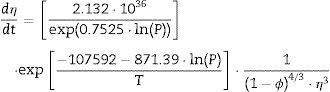
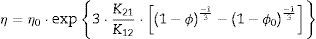
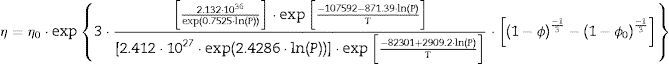
![Determination of the maximum dwell time at specific sintering temperature [40]. Determination of the maximum dwell time at specific sintering temperature [40].](https://static.elsevier.es/multimedia/03663175/0000005700000001/v1_201802131616/S036631751730078X/v1_201802131616/en/main.assets/thumbnail/gr8.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Densification and grain growth rates versus sintering time at 1100°C, comparing a single step-up and a staggered thermal cycle [40]. Densification and grain growth rates versus sintering time at 1100°C, comparing a single step-up and a staggered thermal cycle [40].](https://static.elsevier.es/multimedia/03663175/0000005700000001/v1_201802131616/S036631751730078X/v1_201802131616/en/main.assets/thumbnail/gr10.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)

