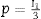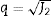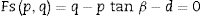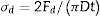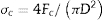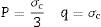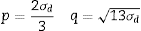En este artículo se ha estudiado el comportamiento mecánico a rotura de compactos en verde de dos tipos de α-SiC con diferentes granulometrías y pureza con objeto de evaluar la variación de los parámetros del criterio de fallo de Drucker-Prager en ambos materiales. Los compactos en verde se fabricaron a presiones de compactación entre 60 y 100 MPa. Estos compactos fueron caracterizados mediante ensayos a rotura a compresión uniaxial y diametral, con lo que modelaron los parámetros del criterio de fallo de Drucker-Prager a diferentes densidades relativas. Los resultados muestran el diferente comportamiento a compresión causado por la geometría de las partículas de cada material.
This paper is concerned with the mechanical behaviour of compacted ceramic green components of two α-SiC with different particle size-shape and purity with the purpose of evaluate the Drucker-Prager criterion in both material. Compaction pressures were between 60 and 100 MPa. The green compact were evaluated by two tests such as diametrical compression and uniaxial compression for different relative densities. These models are used both for die design as for parts design. The results show the different compression behaviour caused by the particles shape of each material.
El carburo de silicio (SiC) es un material cerámico semiconductor. Las características principales del SiC son su elevada resistencia mecánica, el módulo de elasticidad y su alta resistencia a la corrosión y erosión frente a la temperatura, con una baja densidad específica ([1]). Debido a sus propiedades, el carburo de silicio es un material ingenieril con gran abanico de aplicaciones. Debido a la inviabilidad de la fabricación de piezas mediante mecanizado, por sus altas propiedades mecánicas, la técnica de consolidación de polvos es de gran interés en la industria.
Uno de los procesos más habituales de fabricación de piezas a través de la consolidación de polvos es mediante la compactación uniaxial o la compactación isostática ([2]). Durante la compactación uniaxial se consolidan los polvos mediante presión aumentando la densidad aparente del compacto. En el proceso de compactación se describen 3 etapas ([3]) que son comunes e independientes del material en polvo empleado (metálicos, cerámicos, farmacéuticos…): una primera etapa donde se produce un reordenamiento de las partículas, una etapa posterior de deformación elástica y finalmente, según aumenta la presión de compactación, una etapa de deformación plástica durante la cual se produce el endurecimiento por acritud de las partículas.
Un criterio de fallo es un modelo matemático que a partir del estado de tensiones y/o deformaciones de un punto define la rotura del material. Existen numerosos criterios de fallo aplicados en el estudio a rotura de compactos a partir de materiales pulverulentos, como el criterio de Mohr-Coulomb ([4]), de Cam-Clay ([5]) o de Drucker-Prager ([6]). El criterio de fallo de Drucker-Prager ha sido ampliamente utilizado por su versatilidad en polvos metálicos ([7], [8], [9]), cerámicos ([10], [11], [12]) y farmacéuticos ([13], [14], [15], [16], [17], [18], [19], [20]), motivo por el cual se ha empleado en esta publicación.
El criterio de fallo de Drucker-Prager se obtiene a partir del primer invariante del tensor de tensiones y el segundo invariante del tensor desviador (I1, J2). Se emplea el primer invariante para calcular la tensión hidrostática que sufre el material
y el segundo invariante para obtener la tensión efectiva . El criterio de fallo viene dado por una recta en el plano (p,q) que corresponde a la función Fs(p,q) = 0 (ecuación 1). Las características de las partículas (morfología) que integran el polvo, así como la densidad relativa final del compacto, influyen en los parámetros de ajuste del modelo (d, β).donde q es la tensión efectiva, p es la tensión hidrostática, β es el ángulo de fricción y d es la cohesión del material.
En el presente trabajo se va a determinar el criterio de fallo de Drucker-Prager de 2 carburos de silicio α a partir de ensayos a rotura de compresión uniaxial y diametral. Los parámetros característicos que definen la línea de fallo se determinan para diferentes densidades relativas del compacto. Se estudiará la influencia de la morfología de la partícula en el criterio de fallo.
Materiales y fabricación de las probetasMaterialesSe han empleado en el estudio 2 tipos de polvo de carburo de silicio α (SiC), uno de Materion (S-2022, Cerac, pureza 99,9%) y otro de Goodfellow (SI516021, Goodfellow, pureza 99%). El contenido en impurezas hace que el SiC-Materion posea una densidad de 3,16 g/cm3, mientras que el SiC-Goodfellow tiene una densidad de 3,217 g/cm3.
Fabricación de las probetasLos polvos fueron compactados empleando una máquina universal de ensayos (Metrotec MTE-300) en una matriz de acero inoxidable endurecida de diámetro 19,9 mm previamente lubricada.
El llenado de la matriz de compactación fue realizado manualmente acompañado de un posterior vibrado para alcanzar un empaquetamiento uniforme en su interior.
La densidad aparente se ha calculado a partir de las dimensiones de la probeta, su masa y el desplazamiento del pistón de compactación. La densidad relativa (DR) se calcula de la relación entre la densidad aparente (ρ) y la densidad teórica del material sólido (ρfull): DR = ρ/ρfull.
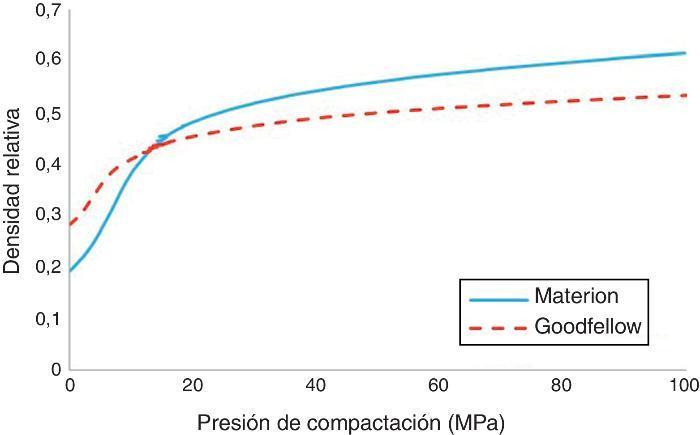
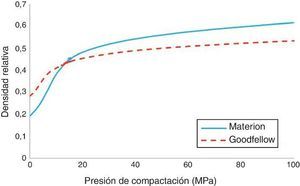
En la Figura 1 se representa como ejemplo la curva de compactación hasta 100 MPa a una velocidad de compactación de 10 mm/min para ambos materiales. Se observa como inicialmente la densidad relativa en SiC-Goodfellow es mayor que el SiC-Materion, y que a partir de 15 MPa la tendencia se invierte, haciéndose asintótico a partir de 80 MPa.
Figura 1. Curvas de compactación hasta 100 MPa realizadas a una velocidad de deformación de 10 mm/min de SiC-Materion y SiC-Goodfellow. Se observa una densidad inicial en el llenado del molde y un comportamiento durante la compactación diferente.
A presiones de compactación superiores a 100 MPa el SiC-Goodfellow presenta fisuras, taponado y laminación, por lo que la máxima presión de compactación empleada ha sido de 100 MPa.
En base a las curvas de compactación las probetas se fabricaron a presiones de 60, 70, 80, 90, 95 y 100 MPa, con una velocidad de 10 mm/min. Las probetas delgadas para el ensayo brasileño se fabricaron con un espesor menor a 4 mm, mientras que el espesor de las probetas para el ensayo de compresión fue de 14 mm. Para cada material, condición de presión y tipo de ensayo se fabricaron 2 probetas. Tras la compactación no se observan defectos visibles.
Metodología experimentalAnálisis granulométricoLa determinación de la distribución del tamaño de partícula se ha llevado a cabo utilizando un analizador láser modelo Mastersizer (Malvern, Reino Unido). Las muestras fueron homogeneizadas y dispersas en etanol.
Microscopia de barridoEl análisis granulométrico se complementó mediante microscopia de barrido (FESEM, S-4700, Hitachi, Japón). Para evitar la carga eléctrica de las muestras, fueron depositadas con oro.
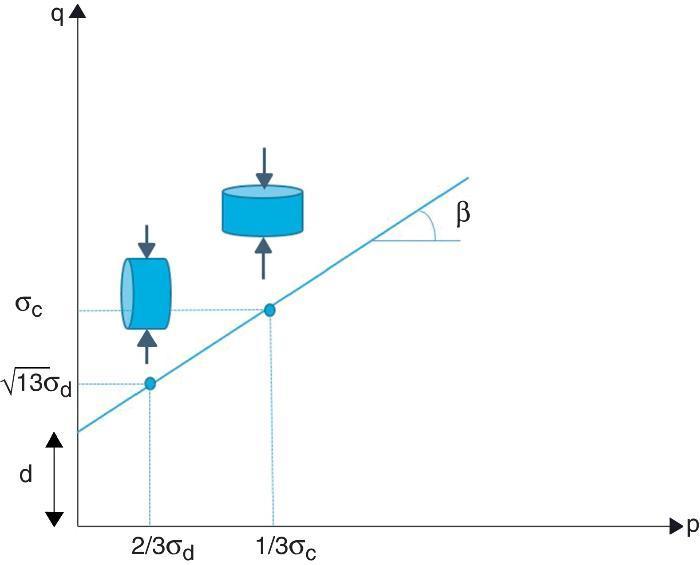
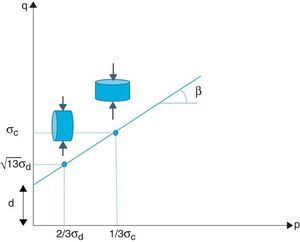
Ensayos a roturaPara la obtención de los parámetros del criterio de fallo de Drucker-Prager, Fs(p,q) = 0, es necesario la caracterización a rotura de los compactos mediante ensayos de compresión uniaxial y compresión diametral (también conocido como ensayo brasileño) a diferentes valores de densidad relativa. Para el ensayo de compresión diametral o brasileño, el ratio H/D ha de ser menor del 0,25 para garantizar que la teoría de Hertz es aplicable ([21], [22], [23], [24], [25], [26]), lo que da lugar a probetas delgadas. Para el ensayo de compresión uniaxial no es necesario ningún requerimiento geométrico. Con ambos ensayos se podrá trazar la línea de fallo según se indica en la Figura 2.
Figura 2. Representación en el plano p-q de los puntos correspondientes a la tensión de rotura de los ensayos de compresión uniaxial y diametral para la determinación de la línea de fallo.
Los ensayos a rotura se realizaron a velocidad constante de 1 mm/min. Tras el ensayo se obtiene el valor de fuerza a rotura de las probetas, que hemos denominado Fc para el ensayo de compresión uniaxial y Fd para el ensayo brasileño. La obtención de las tensiones de rotura se determinan a partir de las ecuaciones 2 (compresión diametral) y 3 (compresión uniaxial) ([22], [26], [27]).
La tensión equivalente p y la tensión efectiva q de los ensayos se calculan con las ecuaciones 4 (compresión uniaxial) y 5 (compresión diametral) ([7]):
Donde σc y σd son las tensiones de rotura de las probetas en el ensayo de compresión y el ensayo brasileño, respectivamente. La línea de rotura está definida por los 2 puntos correspondientes a los ensayos realizados, como se muestra en la Figura 2. La cohesión del material, d, y el ángulo de fricción interna, β, quedaran definidos en la Figura 2 como el punto de corte en el eje de ordenadas y el ángulo de la línea de rotura, respectivamente.
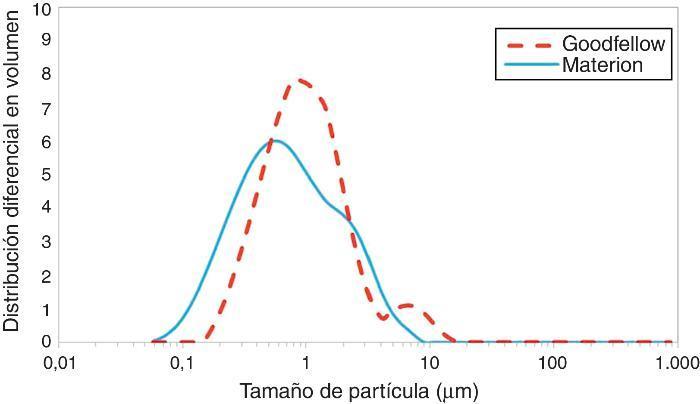
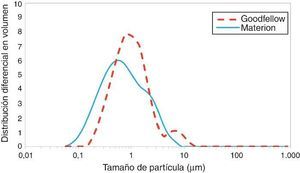
Resultados y discusiónLa Figura 3 muestra la distribución de partículas para cada carburo de silicio. Se puede apreciar una distribución bimodal del tamaño de partícula en ambos materiales debido a que parte del polvo se encuentra aglomerado y esto podría favorecer la compactación en sus etapas iniciales. El SiC-Materion posee una distribución de partículas que varía del d10 = 0,29 μm, d50 = 0,63 μm, hasta d90 = 2,45 μm. El SiC-Goodfellow posee una distribución de partícula de d10 = 0,34 μm, d50 = 0,88 μm, hasta d90 = 2,54 μm.
Figura 3. Distribución de partículas de los 2 carburos de silicio en etanol.
La Figura 4 muestra la micrografía SEM de las partículas del SiC-Materion. Se puede observar la formación de aglomerados de partículas poliédricas en la Figura 4b, llegando a superar las 2 μm de diámetro aparente, y una amplia dispersión del tamaño de partículas en la Figura 4a.
Figura 4. a) Micrografía (×3.500) de los aglomerados de partículas SiC α Materion. b) Micrografía (×25.000) de los aglomerados; se observan partículas poligonales de SiC α Materion.
En la Figura 5 se muestran las micrografías SEM de las partículas de SiC-Goodfellow. En la Figura 5a se observan aglomerados esferoidales (hasta aprox. 30 μm) y toroidales (aprox. 15 μm) característicos del spray-drying, que corresponde a la segunda meseta que aparece en la distribución de partículas (Figura 3). Estos aglomerados están compuestos por partículas laminares, como se observa en las micrografías a mayores aumentos (Figura 5b-d).
Figura 5. a) Micrografía (×1.800) de los aglomerados de partículas SiC α Goodfellow. b-d) Micrografías a mayores aumentos de los aglomerados; se observa la geometría en forma de finas láminas predominante en el SiC α Goodfellow.
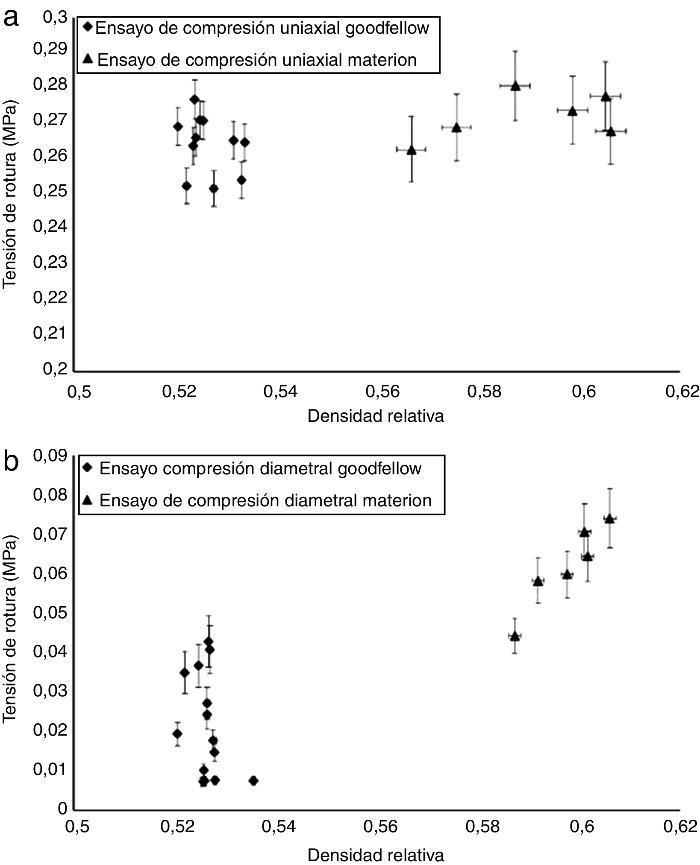
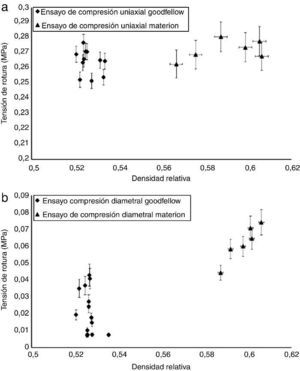
La Figura 6 muestra la tensión de rotura a compresión uniaxial (Figura 6a) y diametral (Figura 6b) en función de la densidad relativa (DR) de cada probeta. Puede observarse que la tensión de rotura a compresión uniaxial (Figura 6a) del SiC-Materion aumenta ligeramente con la densidad del compacto hasta una DR = 0,59; para densidades superiores la tensión de rotura disminuye debido probablemente a la aparición de microgrietas en la probeta. Los resultados obtenidos de tensión de rotura del SiC-Goodfellow no muestran ninguna tendencia.
Figura 6. Tensiones de rotura a compresión uniaxial (a) y compresión diametral (b) frente a la densidad obtenida en los compactos en verde en ambos SiC.
En la Figura 6b se observa la tensión de rotura diametral de ambos materiales. En este caso, la tendencia lineal creciente con la densidad relativa observada en el SiC-Materion contrasta con la dispersión o incluso disminución de la tensión de rotura diametral que se mide en el SiC-Goodfellow.
La Figura 7 muestra las probetas de SiC-Materion y SiC-Goodfellow tras los ensayos de compresión diametral y uniaxial junto con micrografías de la superficie de fractura fresca de las muestras compactadas a 90 MPa. Las Figura 7a-c corresponde a probetas rotas en los ensayos y micrografía de fractura en el SiC-Materion, y las Figura 7d-f son las probetas equivalentes en el SiC-Goodfellow. Las probetas ensayadas a compresión diametral (Figura 7d) y uniaxial (Figura 7e) de Goodfellow muestran un laminamiento del material. Las Figura 7c y 7f muestran las superficies de fractura fresca de ambos materiales, donde se observan superficies lisas correspondientes a la aparición de grietas internas en el SiC-Goodfellow en contraposición a la superficie de Si-Materion.
Figura 7. Fila superior, fotografías de las probetas ensayadas a compresión a) diametral, b) uniaxial y c) micrografía de fractura fresca en el SiC-Materion. Fila inferior, fotografía de las probetas ensayadas a compresión: d) diametral, e) uniaxial y f) micrografía de fractura fresca en el SiC-Goodfellow.
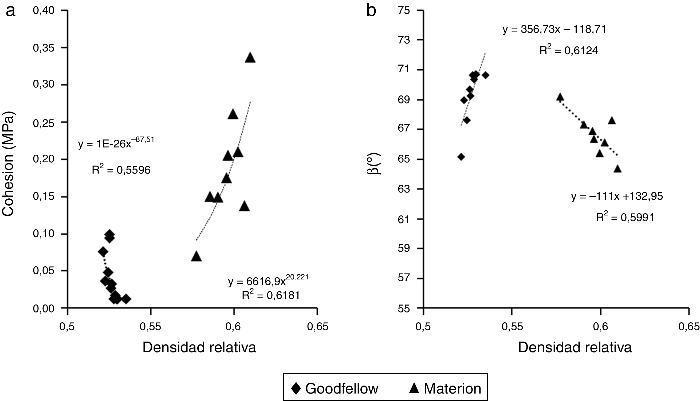
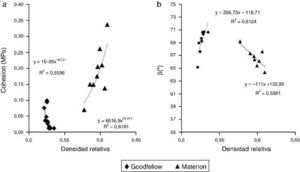
Los parámetros de la línea de fallo (d y β) en función de la densidad relativa se muestra en la Figura 8. Se observa que el valor de la cohesión (Figura 8a) en SiC-Materion es creciente con el incremento de la densidad relativa, y el ángulo de fricción interna (Figura 8b) disminuye. La distribución de partículas y la geometría de este polvo hace que la unión entre partículas sea mayor, lo que incrementa la cohesión (la resistencia a esfuerzos cortantes) entre ellas impidiendo movimientos relativos y disminuyendo el ángulo de fricción. Sin embargo, en el SiC-Goodfellow, aun teniendo una distribución semejante de partículas, la geometría laminar hace que la cohesión (a) disminuya y el ángulo de fricción (b) aumente a medida que la presión de compactación (densidad relativa) se incrementa. Esto es debido a la geometría predominantemente laminar de estas partículas que permite el deslizamiento y facilita los movimientos relativos.
Figura 8. Parámetros de la línea de fallo frente a la densidad relativa del compacto en ambos materiales: a) valores calculados correspondientes a la cohesión (d) junto con la línea de tendencia potencial; b) valores calculados correspondientes al ángulo de fricción β junto a una línea de tendencia lineal.
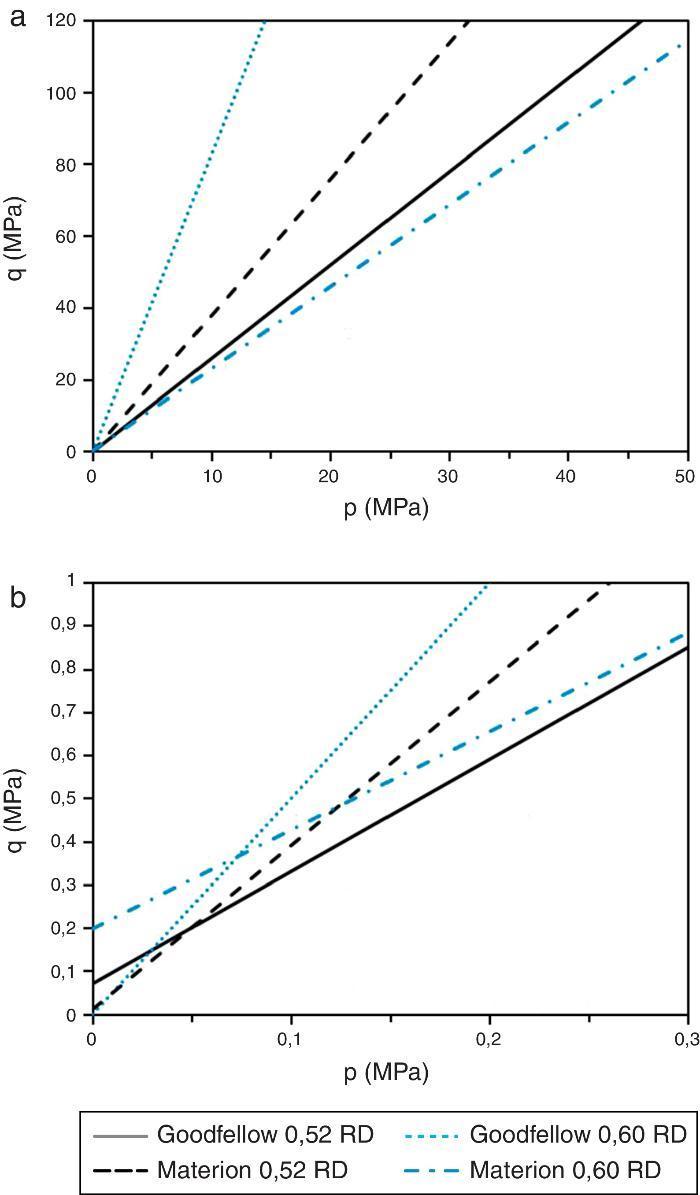
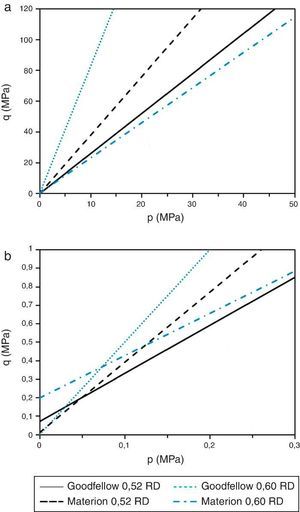
En la Figura 9a y b puede observarse, en el plano p-q, la línea de fallo en ambos materiales a 2 densidades relativas diferentes. La Figura 9a es el aspecto general del criterio de Drucker Prager de estos materiales, y en la Figura 9b se observa en detalle la zona donde el criterio de fallo cruza con el eje de ordenadas donde se define el valor de la cohesión. Puede observase que en el material SiC-Materion al aumento de densidad produce un aumento de cohesión y, por tanto, aumenta su resistencia a esfuerzos cortantes y de tracción, lo que indica que la muestra compactada mejora sus propiedades mecánicas.
Figura 9. Representación en el plano p-q de las líneas de fallo de Drucker-Prager correspondientes a una densidad relativa de 0,52 y 0,60 para el SiC-Goodfellow y SiC-Materion. a) valores de tensión equivalente de 120 MPa; b) detalle hasta una tensión equivalente de 1 MPa para apreciar la variación en la cohesión (d) de ambos materiales.
ConclusionesSe ha caracterizado mediante ensayos a rotura el criterio de fallo de Drucker-Prager de 2 materiales de α-SiC con diferente geometría de partícula a partir del cual se puede predecir el comportamiento mecánico del material en verde. Los parámetros del modelo muestran un comportamiento opuesto en ambos materiales asociado a la geometría de la partícula.
Se ha comprobado que la geometría laminar disminuye la cohesión y aumenta el ángulo de fricción interna de los compactos en verde provocando la aparición de grietas internas e incluso su rotura.
Recibido 26 Octubre 2015
Aceptado 12 Febrero 2016
Autor para correspondencia. bachiaga@nebrija.es