Recently, ferroelectric behavior was observed in compressed SrTaO2N thin films epitaxially grown on SrTiO3 substrates. Piezoresponse force microscopy measurements revealed small domains (101–102nm) that exhibited classical ferroelectricity, a behavior not previously observed in perovskite oxynitrides. The surrounding matrix region exhibited relaxor ferroelectric-like behavior. Bulk SrTaO2N samples do not show ferroelectricity, thus suggesting that the origin of it may be related with the strain induced by the substrate. Ab-initio calculations reported that the small domains and the surrounding matrix had trans-type and a cis-type anion arrangements, respectively, but do not describe the experimentally observed equilibrium phase, nor the strain dependent polarization. In this work, we present high accurate all-electron first-principles calculations on the different possible local structures that can explain the ferroelectric-like properties of the strained material. The determined local structure and oxygen/nitrogen ordering has been related with polarization and epitaxial strain. The potential energies and polarization as functions of the in-plane lattice constant are reported.
Recientemente, se observó comportamiento ferroeléctrico en películas delgadas de SrTaO2N crecidas epitaxialmente sobre sustratos de SrTiO3. En mediciones de microscopía de fuerza piezoeléctrica se observaron pequeños dominios (101-102nm) que exhibieron ferroelectricidad clásica. Este comportamiento no fue observado previamente en oxinitruros de perovskita. La región de la matriz circundante a estos dominios presentaron un comportamiento del tipo relaxor. En muestras macroscópicas de SrTaO2N no fue encontrada ferroelectricidad, lo que sugiere que el origen de la misma puede estar relacionado con el esfuerzo de corte inducido por el sustrato. Cálculos ab-initio realizados previamente parecen concluir que los pequeños dominios ferroeléctricos y la matriz circundante tienen disposiciones de aniones del tipo trans y cis, respectivamente, pero en ellos no se predice la fase de equilibrio observada experimentalmente, ni la polarización neta resultante en la estructura ferroeléctrica dependiente del esfuerzo de corte. En este trabajo presentamos cálculos de primeros principios de alta precisión realizados sobre las diferentes estructuras locales posibles que pueden explicar las propiedades ferroeléctricas del material bajo esfuerzo. La estructura local determinada y el ordenamiento de oxígeno/nitrógeno se han relacionado con la polarización y la deformación epitaxial. Como producto de ello se calcularon las energías potenciales y la polarización neta como funciones de la constante de la red paralela al plano de la interfase.
In the last years AB(O,N)3 oxynitrides have attracted much attention because of their novel electronic functionalities, such as high dielectric constant [1], visible light absorption [2], photocatalytic activity [3] and colossal magneto-resistance [4]. The oxynitrides are formed by the partial substitution of oxygen by nitrogen atoms into the anionic network of the ABO3 perovskite-type compounds (e.g. A=Ca, Sr, Ba or lanthanide, B=Ti, Ta or Nb). The increase of negative charges are compensated with simultaneous cationic substitutions [5–8]. The replacement of some O atoms by N ones may change the color of the initially white powders, so, these compounds have potential application as safe colored pigment material to replace currently used contaminant heavy metals (Cr, Cd, Pb, etc.) containing pigments [9]. The optical properties have been extensively studied. However, the changes in bonding type and local structure that accompany the introduction of N ions may also give rise to interesting dielectric properties. The aliovalent substitution provides a mechanism for enhance the dielectric polarizability through the substitution of more polarizable ions into the lattice [10]. Furthermore, the reduced electronegativity of the N ion respect to the O one, would rise up the covalence character of the cation–anion bonds [1]. The increased covalency of the bonding can in turn increase the likelihood of cation displacements through a second-order Jahn–Teller distortion of the d0 cation [11]. It is well known that such displacements are the origin of ferroelectricity. On the other hand, the mixed occupancy of the anion site in oxynitrides, AB(O1−xNx)3, provides a condition similar to that found in relaxors, as the polarizing octahedral cations will experience random chemical environments in the absence of complete O/N ordering. It is therefore, an interesting issue to examine whether the perovskite oxynitrides possess intrinsically high κ and relaxor-like properties.
The electronic structure of perovskite oxynitrides may be influenced by the geometrical configuration of the O and N atoms around their metal cations. For the case of ABO2N oxynitride, in which each B cation is surrounded by four O and two N ions thus forming a BO4N2 octahedron, there are two possible anion configurations: the two N ions can occupy either (i) adjacent (cis-type) or (ii) opposite (trans-type) sites. Researchers have argued that the dielectric properties of ABO2N are related to anion arrangement. Page et al. [12] suggested that ferroelectricity in trans-type anion-ordered ATaO2N (A=Sr, Ba) phases may be caused by the off-center displacement of Ta ions. They have used different nitrogen arrangements and space groups in order to investigate the stability of oxynitride phases based on theoretical approach. The stability energy for the trans-type phases was higher than the determined for cis-type phases. In fact, the bulk SrTaO2N specimens have been confirmed to exhibit cis-type configurations with I4mcm space group [13,14]. Recently, different ferroelectric and relaxor regions were detected in thin films samples of SrTaO2N epitaxially grown on a SrTiO3 substrate [15,16]. The lattice mismatch between the oxynitride and the substrate is responsible of the strain parallel to the interface thus reducing the in-plane lattice constant when it is grown as thin film, favoring the stabilization of a trans-type polar P4mm ferroelectric structure [12,15].
Computational quantum-mechanical simulations have proven to be a suitable tool for understanding the microscopic processes that are responsible of the physical properties of materials. Beyond the simplicity of the models, in comparison to the complexity of real materials especially in disordered and ceramic materials, they can lead to a good description of individual processes involved. Although some previous studies on the phase stability in bulk SrTaO2N have been published [12,15,17], there are still open questions regarding the calculated phase diagrams. In the work of Page et al. and Oka et al., the experimentally stable I4mcm phase appear third in order of stability taking into account the total energy at zero pressure. The phase diagram shows that the non polar I4mcm structure and the trans-polar P4mm are very close in energy. This small difference may require the use of high precision methods to resolve between.
It is well known that within the pseudopotential methods for the calculations of the electron density, the selection of the function to represent the potential of the valence electrons may play a crucial role. This problem is not present in all-electron methods. In this work, the phase stability diagram at zero pressure is discussed considering different approaches to the Density Functional Theory (DFT) [18] by means of high precision all-electrons, and also pseudopotential methods in order to compare results and interpret the phase stability diagram. Furthermore, the ferroelectric distortion in the P4mm phase was analyzed in order to study the resulting net dipole moment as a function of the in-plane lattice parameter. The paper is organized as follows: in the second section, the computational methods are described. In the third section, the results of the calculations are shown. The fourth section is reserved to the Discussion and finally on the fifth section we present our Conclusions.
Methods of calculationsIn order to determine the structural ground state of the strontium tantalite oxynitride (SrTaO2N) different crystal structures were considered using two different ab initio approximations to solve the Kohn-Sham equation in the framework of the Density Functional Theory: (i) the full-potential linear augmented plane wave plus local orbital (FP-APW) method in a scalar relativistic version [19], WIEN2k code [20] and (ii) plane wave and pseudopotential method, Quantum ESPRESSO (QE) code [23]. For the WIEN2k code, the energy cut-off criterion RKM (RKM=RmtKmax, where Rmt denotes the smallest muffin-tin radius and Kmax the largest wave number of the basis set) was carefully investigated, finding that normal values such as RKM=7 or 8 do not produce the correct stable solution. Higher values such as RKM=10 were implemented. Integration in reciprocal space was performed using the tetrahedron method [21] considering up to 3000 k-points in the full Brillouin zone (BZ), which are reduced to different numbers depending on the symmetry of the different structures, in the irreducible edge of the BZ (IBZ). On the other hand, for the Quantum ESPRESSO (QE) code, a kinetic energy cutoff of 75Ry and a charge density energy cutoff of 825Ry were used. The IBZ was sampled using the Monkhorst–Pack scheme [25] with a 10×10×10mesh. Vanderbilt ultrasoft pseudopotentials were used [24].
For both methods the electronic exchange–correlation potential (XC) used was described by the Perdew–Burke–Ernzerhof parameterization of the generalized gradient approximation (GGA-PBE) [22]. For each structure internal atomic the atomic positions were optimized until the residual force acting on all atomic coordinates was less than 0.01eV/Å.
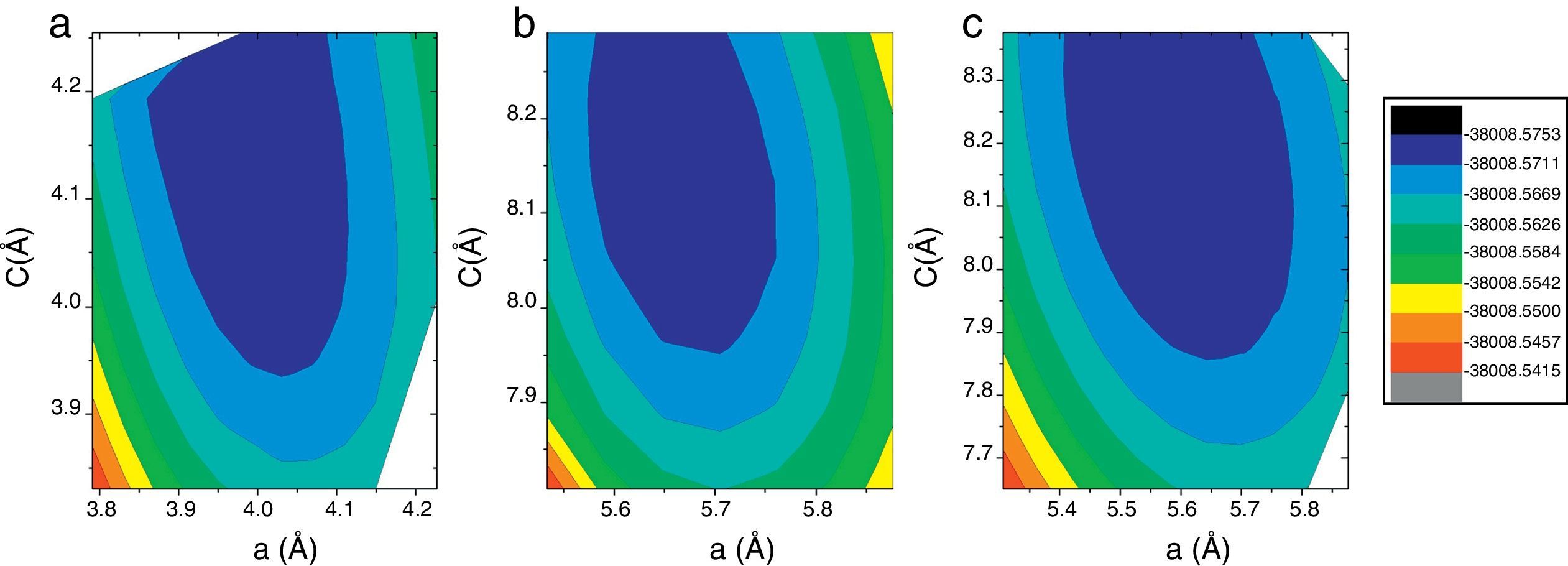
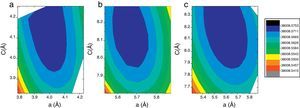
ResultsWe have performed self-consistent total energy calculations on the I4mcm, P4mm, Pbmm, I4mmm, and Pm3m phases as a function of the in-plane lattice parameter by using the all-electron method FP-APW. In order to understand why the experimentally determined I4mcm phase at zero pressure is not the predicted as the more stable phase by theoretical calculations [12,15], we have also calculated the total energy for the three first structures using QE to compare our results with the previously reported using pseudo-potential methods [12,15]. In all cases the whole atomic positions were relaxed as described in the previous section. A total energy contour plots using a 10×10mesh for the a and c values was constructed in order to obtain the lattice constants corresponding to the ground state. In Fig. 1 we present the obtained results using FP-LAPW on the tetragonal structures, in which a clear minimum can be observed for each one. Lattice constants for the tetragonal I structures with regards to the P4mm are: a=2a′ and c=2c′. The orthorhombic Pbmm structure has 3 degrees of freedom due to the independent variation of the a, b and c lattice constants. For the latter calculations we performed using a 5×5×5grid. The cubic Pm3m structure has only one degree of freedom due to a=b=c. The calculation for these lasts cannot be presented as a two-dimensional contour plot.
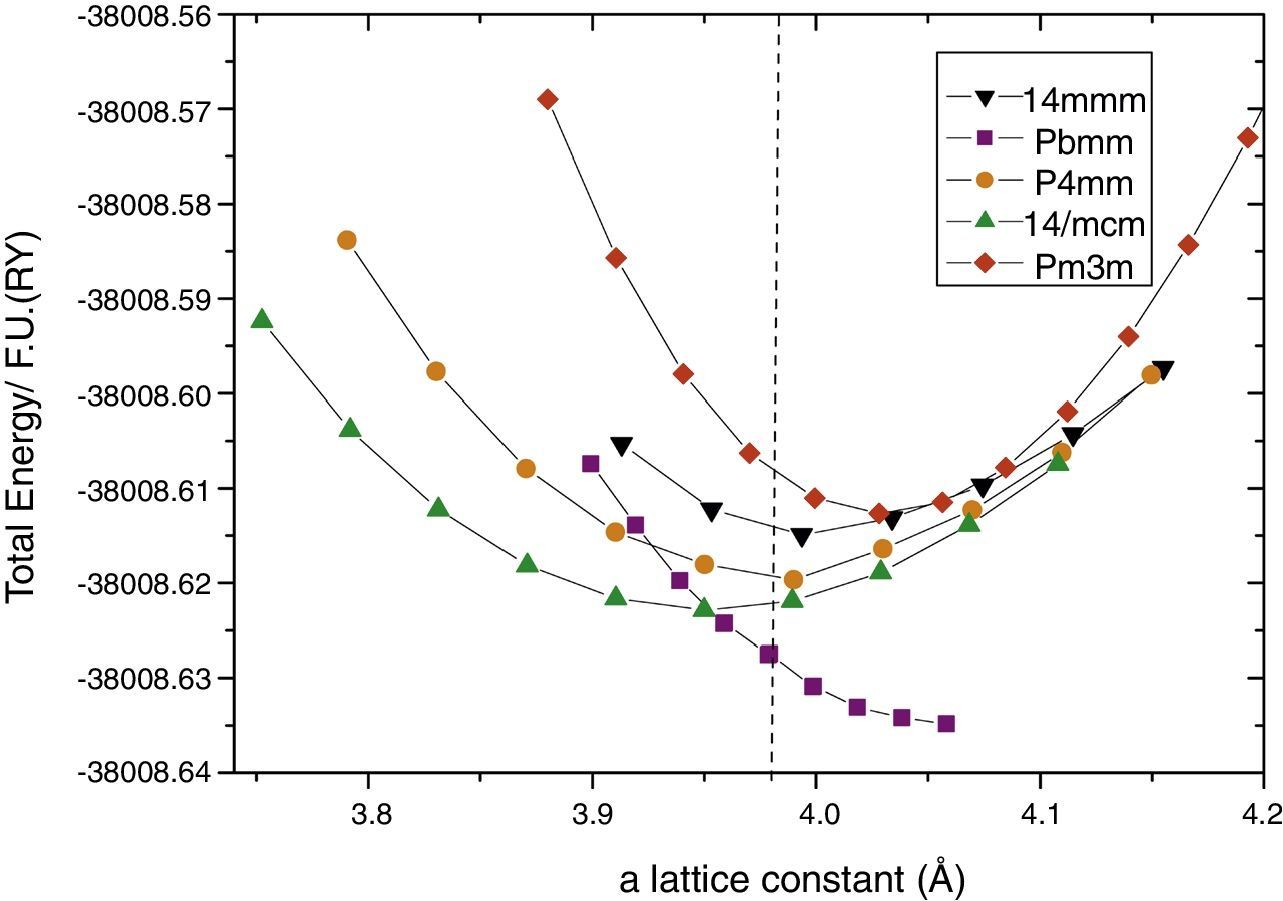
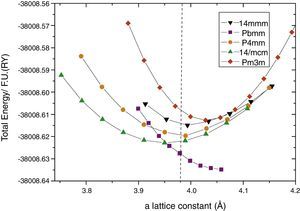
Then, for each one of the relaxed structures, we selected that with the minimum energy for each in-plane a lattice constant value for the different considered c values, and the total energy vs. a plot were constructed. By doing this, we observed that due the small energy differences between the P4mm and the experimentally observed I4mcm phases, the obtained stable structure resulted highly sensitive to the convergence parameters and the method of calculation. For the case of the FP-APW the RKM parameter hardly scales the computing resources and time. For this method, both curves cross as far as the RKM values are incremented up to 9. Tests on selected cells using highly computing demanding with RKM=10 do not showed significant differences on the final results. The obtained results are presented in Fig. 2. It can be seen that using this high-precision method, the non-polar I4mcm structure is energetically below the polar P4mm. This result is encouraging nevertheless the Pbmm structure still remains lower in energy.
The total energy per formula unit of each structure, under epitaxial strain calculated with all-electron FP-APW method; Pbmm cis (squares), I4/mcm trans (green up triangles), P4mm trans (yellow circles), cis I4mmm (black down triangles) and trans Pm3m (red rhomb). Out-of-plane lattice constants were optimized for each point.
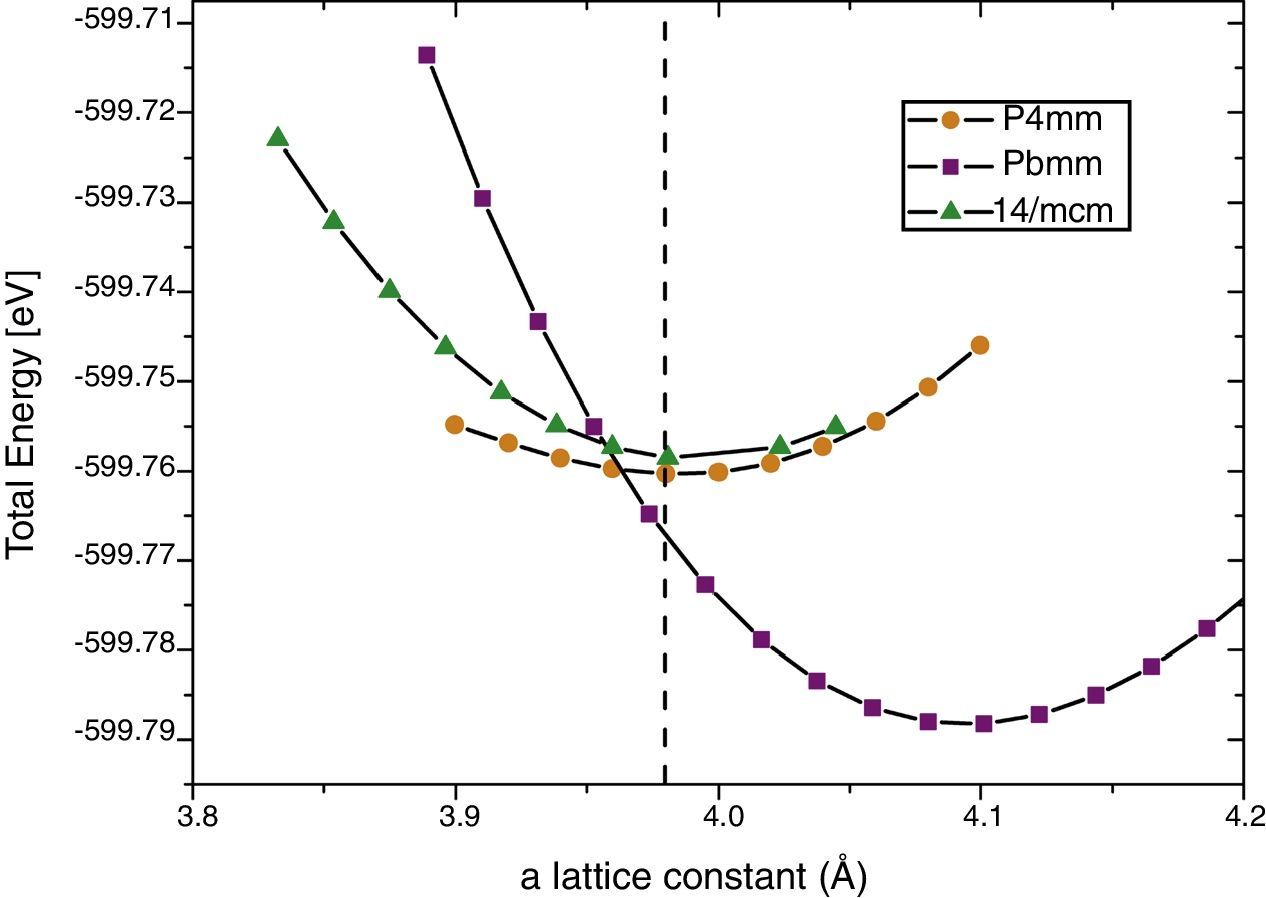
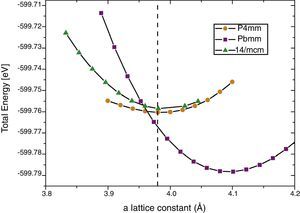
Calculations performed using pseudopotentials by means of QE using the same exchange-correlation potential are depicted in Fig. 3. The results are similar as the previously reported, i.e., experimental I4mcm structure results with higher energy than P4mm for all a. Thus, it seems that the reason of this inconsistency must rely in the pseudopotential selection which becomes important to correctly describe such small energy differences.
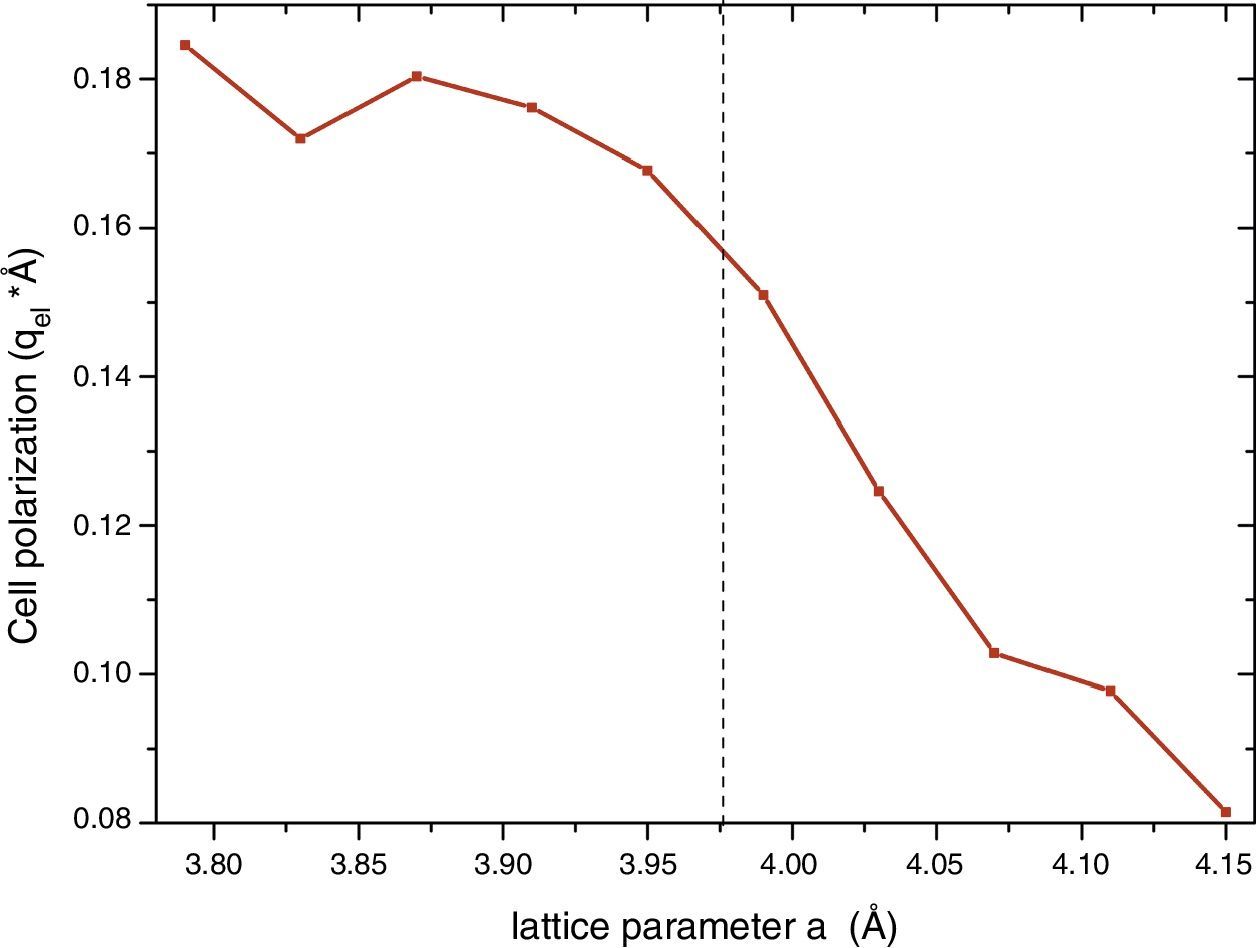
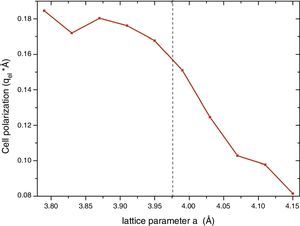
The detection of ferroelectricity in regions of in-plane strained samples, as they were grown on a substrate with smaller lattice constant, should be related with the stabilization of the trans P4mm phase which is the unique within this group of structures that presents a net electric dipolar moment. Other scenarios are also possible with other structures with cis-type N arrangement, but they correspond to much bigger structures out of the scope of these calculations. Then, we analyzed the net polarization of the P4mm ferroelectric structure. Once the smaller energy structure was obtained for each a value, we calculated the charge center taking into account the ion optimized positions. This procedure in principle can be used to select the substrate in order to optimize the polarization of the strained sample. The results are shown in Fig. 4. It can be seen that at the experimental lattice a=3.98Å [15] the net dipole moment is about 0.16qel*Å, where qel stands for the electron charge module. Also, it can been observed that in principle the dipole moment module can be augmented up to 0.18 for smaller a values. Up to this value the polarization seems to saturate, nevertheless the c/a tetragonal distortion continuously augments (not shown). This result indicate that in principle the net dipole moment could be enhanced by growing the oxynitride over another substrate with larger lattice mismatch.
DiscussionSamples of SrTaO2N present different types of defects. Not only impurities, vacancies, and in the case of ceramic samples, grain boundary charge-trapping, as often found in perovskite materials, but also in the case of oxynitrides the substitution of one of three oxygen atoms by a nitrogen should present different types of cis and trans local arrangements that might stabilize locally different structures out of equilibrium. This fact was discussed in a recent work on the isovalent compound BaTaO2N using Neutron Diffraction Pair Distribution Function Analysis. [12] They found that nevertheless for the long range neutron diffraction Rietveld analysis there is no evidence of O/N ordering in the cubic phase, the local structure appears to favor a cis configuration of the TaO4N2 octahedra with small Ta displacements toward the N atoms. Beyond the complexity of the real materials, the studies of pure systems by means of computational models have proven to be a powerful tool in order to describe microscopic processes.
In this and previous first-principles calculations, the analysis of the total energy for the different structures are performed at 0K. To study the finite temperature phase stability with the present method, huge phonon calculation must be done, as shown in the work of Sanna et al. [26] regarding the phase transitions series of BaTiO3, in order to take into account the vibrational contribution to the Gibbs free energy. In their work the minimum energy difference between cubic and tetragonal phases at 0K was about 48meV (Fig. 1 in the reference) favoring the tetragonal structure. In the case of our study in SrTaO2N, previous reports and the present work find the anti-polar cis Pbmm structure energy minimum about 10meV below the experimentally observed I4mcm phase. Up to our knowledge there are no experimental studies of this compound at low temperatures to account for the stabilization of this phase and further experimental assays would be valuable.
It must be mentioned that in the well know work of Zhong and Vanderbilt [27], it is shown by Quantum Montecarlo methods that quantum fluctuations completely suppress the ferroelectric transition in SrTiO3, and reduce the anti-ferrodistortive transition temperature from 130 to 110K, while for BaTiO3 they do not affect the order of the transition, but do reduce the transition temperature by 35–50K. Thus, the quantum treatment of the O and N ions may play an important role studying these kind of compounds closely related to SrTiO3.
ConclusionsWe report for the first time the net polarization of the ferroelectric structure in SrTaO2N. As mentioned by Oka et al. [15] thin films of this compound were epitaxially grown on SrTiO3 substrate, and regions (10–100nm) with ferroelectric behavior have been detected. They determined that the SrTaO2N structure stabilizes with an in-plane strained lattice constant a=3.98Å. From the calculation of the net polarization of the relaxed P4mm structure as a function of a it can be seen that the parameter for this especial a is close to the maximum value after saturation at 0.18qel*Å. Thus, little enhancement should be expected using different substrates with higher lattice mismatch.
On the other hand we observe that phase stabilization analysis for this compound require high precision calculations in order to evaluate the energy difference between the polar trans P4mm and the non-polar I4mcm. We needed high convergence parameters and the utilization of an all-electron FP-APW method to reproduce the I4mcm structure with small but lower total energy than the ferroelectric P4mm.